domino triangeluarra
Domino triangeluar hau 1995ean sortu zuen Llorca Hnos. S.L. enpresak. Domino triangeluarrak (horietatik hau aldaera bat da) gutxienez 1886. urtetik datozkigu, Troy-ko (New York) Frank H. Richards-ek domino triangeluar bat argitaratu baitzuen.

Osagaiak eta hasiera
Fitxak triangelu aldekideak dira. Hiru aldeen erdialdean puntuak agertzen dira, 0, 1, 2, 3 eta 4. Triangeluen erpinetan zirkunferentzia-arkuak ikus daitezke. Guztira 36 fitxa dira.
Bi eta sei arteko jokalarik har dezakete parte.
Bi jokalarirentzat 12na fitxa banatuko dira eta beste 12ak lapurtzeko utziko dira.
Hiru jokalarirentzat 12na fitxa banatuko dira.
Lau jokalariri 9na fitxa emango zaizkie.
Bost jokalarik 7na fitxa hartuko dituzte eta 0-1-2 fitxa jokoz kanpo utziko da.
Azkenik, sei jokalariri 6na fitxa banatuko zaizkie.
Helburua fitxarik gabe geratzea da. Baina, inork ez badu lortzen, eskuan puntu gutxien duenak irabaziko du.
Arauak
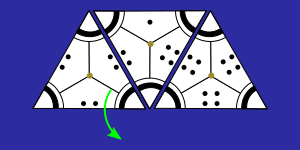
Jokaldia 4-4-4 fitxa duenak hasiko du fitxa hori mahaian utziz. Gero ezkerretik eskuinera pasatuko da txanda. Fitxa horrek hiru alde berdinak dituenez aukera bakarra ematen du beste fitxa batekin lotzeko.
Hurrengo jokalariak beste fitxa bat jarriko du aurrekoaren ondoan, domino arruntean bezala lotuz. Bi fitxek erronboa osatuko dute, lau alde libre utziz. Bestalde, lotutako aldeen erpinek zirkunferentzia-arkuak bikoiztu dituzte.
Ondoren, hirugarren fitxa jarriko da mahaian, aurreko erronboari alde batean lotuz. Horrela trapezio bat osatuko du eta hiru fitxen erpinek zirkunferentzierdia osatuko dute. Fitxa horrek segitu beharko den noranzkoa zehaztuko du, jarri den azken fitxatik abiatuz zirkunferentzia osatu arte.
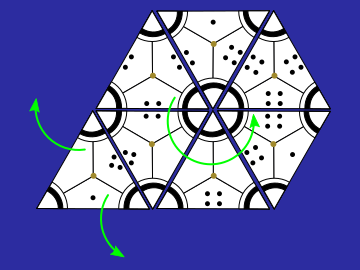
Zazpigarren fitxak bi bide ireki ditu.
Seigarren fitxak zirkunferentzia itxiko du, hexagono bat osatuz eta sei aukera utziz zazpigarren fitxa kokatzeko. Seigarren fitxa jarri duenak zazpigarrena ere jarriko du.
Horrek zirkunferentzia berri bat osatzeko bi aukera utziko ditu, azken fitxaren bi alde libreak hain zuzen. Hurrengo kasuetan ere zirkunferentzia ixten duenak hurrengo fitxa jarriko du. Gerta daiteke jartzen duen hurrengo fitxak zirkunferentzia bat osatzea; orduan, beste fitxa bat jartzeko aukera izango du.
Hurrengo fitxak itxi behar den zirkunferentzia eta noranzkoa zehaztuko ditu. Horrela segituko dute ahal den bitartean.
Jokalari batek fitxa bat kokatu ondoren gainerakoak pasarazten baditu, ez da egongo behartuta zirkunferentzia berarekin jarraitzeko.
Jokoan zehar zirkunferentzia batzuk agertuko dira ustekabean eta gerta daiteke osatzeke geratzea.
Jokoa bi eratan buka daiteke: jokalari bat fitxarik gabe geratzen denean, bera da irabazlea. Fitxa gehiagorik ezin dutenean jarri, orduan puntu gutxien duenak irabaziko du.
Puntuaketa domino arruntean bezala egin daiteke.
Domino honek 36 fitxa ditu eta bost kopuru: zuria, 1, 2, 3 eta 4. Fitxek sortzen dituzten 108 posizio, aldiz, ezin dira bete bost zenbakirekin modu berdinean. Horrek esan nahi du domino hau ez dagoela orekatuta.
Fitxetan agertzen diren puntuak kontuak hartzen baditugu, banaketa hau daukagu:
| Denak | Simetrikoak | |||
| agerpenak | fitxak | agerpenak | fitxak | |
| zuriak | 22 | 16 | 15 | 9 |
| 1ekoak | 22 | 16 | 15 | 9 |
| 2koak | 22 | 16 | 15 | 9 |
| 3koak | 21 | 15 | 15 | 9 |
| 4koak | 21 | 15 | 15 | 9 |
| 108 | 75 | |||
Hau da, 3 eta 4 puntuko aldeak gutxiago agertzen dira.
Domino arruntetan, aukera guztiek agerpen kopuru bera dute eta fitxa kopuru berdinean daude. Bestalde, fitxak komeni den eran elkar daitezke, hots, 1-2 edo 2-1; hortaz, 1-2 fitxa bakarrarekin bi aukera ditugu.
Domino arrunten propietate horiek gorde nahiko bagenitu domino triangeluarrean, ikusi beharko genuke fitxa bat biratzean zenbat fitxa baliokide ematen digun eta ea puntuen kopuruen ordenak eragina duen fitxak osatzean.
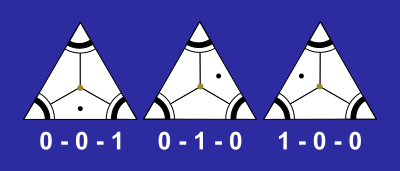
Adibide honetan ikus dezakegu 0 – 0 – 1 fitxa biratzen badugu, 0 – 1 – 0 eta 1 – 0 – 0 fitxak sortzen dituela; beraz, hiru aukera horiek fitxa bakar batekin lortzen ditugu.
Orain, kopuru desberdinekin egingo dugu: adibide honetan ikus dezakegu 0 – 1 – 2 fitxa biratzen badugu, 1 – 2 – 0 eta 2 – 0 – 1 fitxak sortzen dituela; beraz, hiru aukera horiek fitxa bakar batekin lortzen ditugu. Baina horien artean ez dago 0 – 2 – 1 fitxa. Hortaz, azken horretarako beste fitxa bat behar dugu.
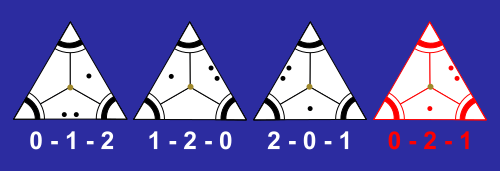
Azken adibidean esandakoak eragina du jokoan. Esaterako, 0 – 1 – 2 fitxa beste bi fitxarekin elkartu nahiko bagenu, fitxa bakar batekin ez genuke beti aukerarik izango.

Hortaz, lirudike puntuen hiru kopuru desberdinak elkartu nahi ditugunean, bi fitxa beharko genituzkeela. Ez du horrela egin hemen aurkeztu dugun domino honek. Fitxen simetria guztiak kontuan hartuz, domino triangeluar orekatu batek 45 fitxa izan beharko lituzke.
Domino honen egileek, itxuraz, honela aukeratu dituzte fitxak: hiru aldeetan kopuru berdinak dituzten fitxak (5 guztira); bi aldetan kopuru bera duten fitxak (20 guztira); hiru kopuru desberdin dituzten fitxak, baliokideak hartu gabe (10 guztira); eta, azkenik, 36 fitxak osatzeko, hiru kopuru desberdin dituen beste fitxa bat, aurreko hamarretako baten simetrikoa, 0 – 1 – 2 fitxa hain zuzen.
Ondoko taulan, dominoaren fitxak ikus ditzakegu. Koloretan daude domino triangeluarrean dauden fitxak. Horien artean daude hiru aldeetan puntuen kopuru berdinak dituzten fitxak (berde ilunak), bi aldetan puntuen kopuru berdinak dituzten fitxak (berde argiak) eta hiru aldeetan puntuen kopuru desberdinak dituzten fitxak (laranjak) eta azkenik erantsitako fitxa (urdina). Gorriz idatzi ditugu domino triangeluarrean ez dauden eta dominoa orekatzeko beharrezkoak diren fitxak.
| 0 | 0 | 0 | 1 | 1 | 4 | ||||||
| 0 | 0 | 1 | 1 | 2 | 2 | ||||||
| 0 | 0 | 2 | 1 | 2 | 3 | 1 | 3 | 2 | |||
| 0 | 0 | 3 | 1 | 2 | 4 | 1 | 4 | 2 | |||
| 0 | 0 | 4 | 1 | 3 | 3 | ||||||
| 0 | 1 | 1 | 1 | 3 | 4 | 1 | 4 | 3 | |||
| 0 | 1 | 2 | 0 | 2 | 1 | 1 | 4 | 4 | |||
| 0 | 1 | 3 | 0 | 3 | 1 | 2 | 2 | 2 | |||
| 0 | 1 | 4 | 0 | 4 | 1 | 2 | 2 | 3 | |||
| 0 | 2 | 2 | 2 | 2 | 4 | ||||||
| 0 | 2 | 3 | 0 | 3 | 2 | 2 | 3 | 3 | |||
| 0 | 2 | 4 | 0 | 4 | 2 | 2 | 3 | 4 | 2 | 4 | 3 |
| 0 | 3 | 3 | 2 | 4 | 4 | ||||||
| 0 | 3 | 4 | 0 | 4 | 3 | 3 | 3 | 3 | |||
| 0 | 4 | 4 | 3 | 3 | 4 | ||||||
| 1 | 1 | 1 | 3 | 4 | 4 | ||||||
| 1 | 1 | 2 | 4 | 4 | 4 | ||||||
| 1 | 1 | 3 |
Iturriak
Eskuko arauak: Llorca Hnos. SL.
