Canastota-ko (New York) postaburu Noyes Palmer Chapman-ek asmatu zuen buru-hausgarria. Esaten denez, 1874an, jada, 16 blokez osatutako buru-hausgarri bat erakutsi zien lagunei, 16 blokeak elkarrekin jarri behar ziren lau blokeko ilaratan, bakoitza 34 batuz, karratu magikoan bezala. Fifteen puzzle hobetuaren kopiak Siracusa-ra, New Yorkera, iritsi ziren Noyesen seme Frank-en bidez, eta handik, hainbat konexioren bidez, Watch Hill-era, Rhode Island-era, eta, azkenik, Hartford-era (Connecticut). Han, Gorren Eskola Amerikarreko ikasleak 1879an puzzlearen fabrikatzen hasi ziren, eta bertan eta Boston-en (Massachusetts) saldu zuten. Horietako bat ikusi ondoren, Matthias Rice, Bostoneko luxuzko arotz-negozio baten zuzendaria, 1879ko abenduan hasi zen buru-hausgarria egiten, eta Yankee Notions luxuzko artikuluen banatzaile bat konbentzitu zuen, gem puzzle izenarekin saltzeko. 1880ko urtarrilaren amaieran, Charles Pevey-k, Worcester-eko (Massachusetts) dentistak, arreta irabazi zuen dirua eskaini baitzuen hamabost buru-hausgarriaren soluzio bat aurkitzeko.

Jokoak eromena ekarri zuen Estatu Batuetara 1880an.

Noyes Chapmanek patente bat eskatu zuen 1880ko otsailaren 21ean bere block solitaire puzzle jokoarekin. Hala ere, patente hori ukatu zioten, ziur aski ez zelako aski desberdina Ernest U. Kinsey-ri 1878ko abuztuaren 20an emandako puzzle-blocks jokoaren patentetik.

Samuel Loyd-ek (1841-1911) 1891tik 1911n hil zen arte esan zuen berak asmatu zuela buru-hausgarria:

The older inhabitants of Puzzleland will remember how in the early seventies 1 drove the entire world crazy over a little box of movable blocks which became known as the 14-15 Puzzle.

Puzzlelandeko biztanle zaharrenek gogoratuko dute nola, hirurogeita hamarreko hamarkadaren hasieran, mundu osoa zoratu nuen 14-15 puzzle izenarekin ezagutzen zen bloke irristagarrien kutxa txiki batekin.

Hala ere, Loydek ez zuen zerikusirik buru-hausgarriaren hasierako asmakuntzarekin edo ospearekin, eta, nolanahi ere, eromena 1880an izan zen, ez 1870eko hamarkadaren hasieran. Loyden buru-hausgarriari buruzko lehen artikulua 1886an argitaratu zen, eta 1891ra arte ez zuen esan, lehen aldiz, asmatzailea  bera zela.

Geroago, Loydek zehaztutako konbinazio berezi bat lortzeko soluzioren bat eman zezakeen edonori eskainitako 1.000 dolarreko sariaren eskaintzak bultzatu zuen interesa jokoan. Konbinazio zehatz hori 14 eta 15 zenbakien trukean zetzan. Loydek 14-15 puzzle deitu zion horri. Hura ezinezkoa zen, hamarkada bat baino lehenago Wm. Woolsey Johnson-ek eta William E. Story-k Notes on the 15 Puzzle, American Journal of Mathematics, (1879) artikuluan frogatua zuten bezala.

Hasierako berriemaileek deskribatzen zutenaren arabera, jokoaren hamabost piezak zoriz jartzen ziren 4×4 marko karratuaren barruan; ondoren, ohiko mugimenduekin piezak zenbakien ordena gorakorraren arabera jarri behar ziren. Horrela planteatuta, Johnsonek eta Storyk frogatu zuten zoriz jarritako posizio guztien erdiak soluzioa zuela,  eta beste erdiak ez. Piezen zorizko posizio batek  soluzioa duen ala ez zehazteko modurik errazena piezak beren posizio zuzenetan jartzeko behar den aldaketa kopurua zenbatzea da. Kopurua bikoitia bada, soluzioa du; bakoitia bada, ezinezkoa da. Badirudi hori nahiko goiz berrezarri zela (bai eta argitaratu ere) eta Warrenek iradokitzen du betirako modu berri bat The Nation kazetan, 1880an:

1. Bota pieza guztiak mahai baten gainean eta ziurtatu ahoz gora daudela guztiak.

2. Itxi begiak eta nahasi pieza guztiak.

3. Jarri pieza guztiak kutxan, begiak itxita. Jakina, pieza batzuk ezkerrera, eskuinera edo aurrera begira egongo dira.

4. Ireki begiak eta kontatu berehala zenbat truke egin behar diren buru-hausgarria ebazteko (14 da maximoa).

5. Kopurua bikoitia bada, biratu piezak zuri begira jarri eta, gero, buru-hausgarria ebatzi. Kopurua bakoitia bada, lehenengo, biratu kutxa osoa 90º erlojuaren orratzen noranzkoan (edo erlojuaren orratzen kontrako noranzkoan), gero biratu piezak eta ebatzi buru-hausgarria lehen bezala.

6. Fintasun erantsi gisa, kutxa osoaren biraketa saihesteko, 6 pieza biratu behar da 9 bihurtzeko, eta 9 pieza biratu 6 bihurtzeko. Hori ezinbestekoa izango da kopurua bakoitia denean, eta beste pieza guztiak zuzentzean egin daiteke.

Teorema matematiko batek erakusten du ez duela axola nola edo zein ordenatan egiten diren trukeak —horiek errepikatu ere egin daitezke—, proba horrek beti emango du erantzun zuzena.

Trukeak kontatzeko modu erraz bat truke-ziklo bat kontatzea da, honela:

a) 1 zenbakidun pieza jaso eta dagokion tokian jarri, bertan dagoen pieza kenduta.

b) Errepikatu (a) kendutako piezaren zenbakiarekin.

c) Jarraitu zenbaki bat hutsik dagoen espazio batera igaro arte, eta horrela zikloa amaitu. Kontatu zikloko truke kopurua. Truke kopurua beti da zikloaren pieza kopurua baino bat txikiagoa.

d) Zenbaki desordenatuak geratzen badira, hasi beste ziklo bat eta jarraitu zenbaki guztiak behar bezala jarri arte. (Praktikarekin, metodo hau buruz egin dezakeen gutxi).

Bigarren bide bat hau da: zenbaki guztiak ordenaturik daudenean, errenkadak korrituko ditugu lehenengo errenkada eskuinera, bigarren errenkada ezkerrera, hirugarren errenkada eskuinera eta laugarrena ezkerrera; orain, zenbakiak ordena horretan idatziko ditugu: 1 – 2 – 3 – 4 – 8 – 7 – 6 – 5 – 9 – 10 – 11 – 12 – 15 – 14 – 13. Orain, transposizioen kopurua zenbatuko dugu. transposizio bat agertzen da zenbaki bikote batean handiena lehenago agertzen denean. Zerrenda horretan hauek dira transposizioak: 8-7, 8-6, 8-5, 7-6, 7-5, 6-5, 15-14, 15-13 eta 14-13; guztira bederatzi transposizio. Emaitza orokorrak dio posizio batetik beste posizio batera igaro daitekeela bi posizioen transposizioen kopuruak bikoitiak direnean, edo biak bakoitiak direnean.

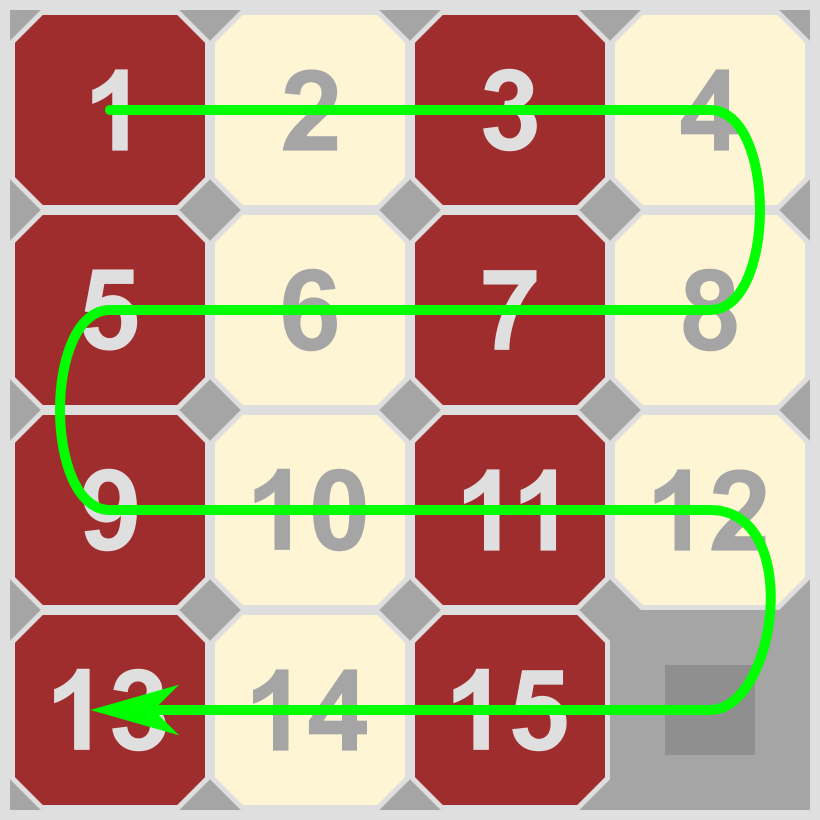
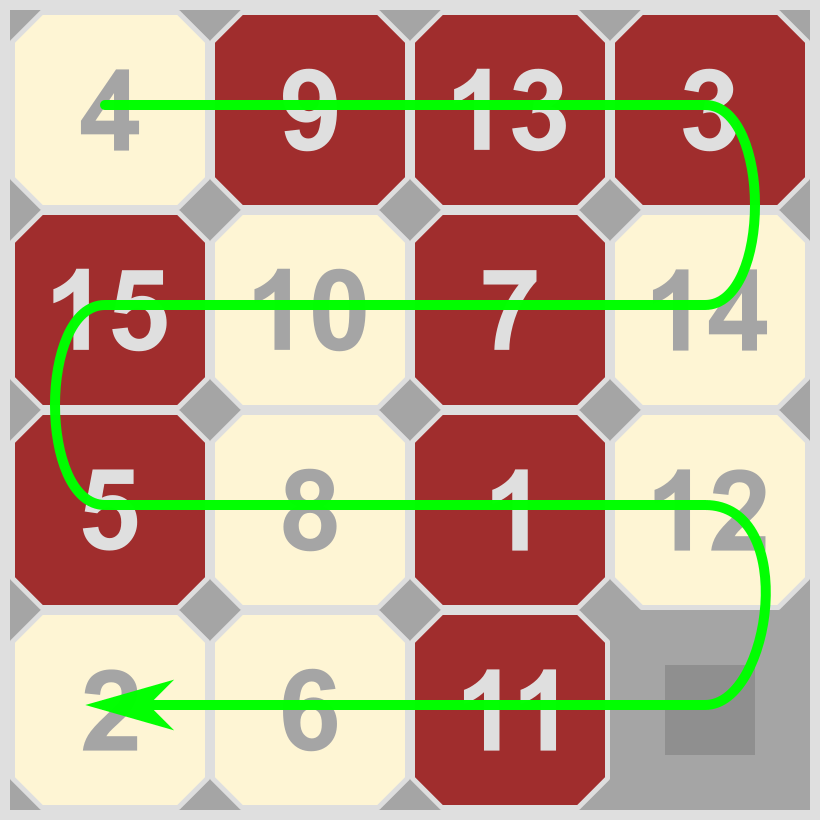
Zorizko posizio batekin antzera egin eta transposizioen kopurua zenbatu; kopurua bakoita denean, hasierako posiziora igaro daiteke: 4 – 9 – 13 – 3 – 14 – 7 – 10 – 15 – 5 – 8 – 1 – 12 – 11 – 6 – 2. Zorizko posizio horretan dauden transposizioak: 4-3, 4-1, 4-2, 9-3, 9-7, 9-5, 9-8, 9-1, 9-6, 9-2, 13-3, 13-7, 13-10, 13-5, 13-8, 13-1, 13-12, 13-11, 13-6, 13-2, 3-1, 3-2, 14-7, 14-10, 14-5, 14-8, 14-1, 14-12, 14-11, 14-6, 14-2, 7-5, 7-1, 7-6, 7-2, 10-5, 10-8, 10-1, 10-6, 10-2, 15-5, 15-8, 15-1, 15-12, 15-11, 15-6, 15-2, 5-1, 5-2, 8-1, 8-6, 8-2, 12-11, 12-6, 12-2, 11-6, 11-2 eta 6-2; guztira, 58 transposizio, bikoitia. Hortaz, zorizko posizio horrek ez du soluziorik, hau da, ezin da hortik hasierako posiziora igaro.

Nahiko izango da zorizko posizio horretan  6 eta 11 zenbakiak trukatzea soluzioa duen posizio bat lortzeko: 4 – 9 – 13 – 3 – 14 – 7 – 10 – 15 – 5 – 8 – 1 – 12 – 6 – 11 – 2. Aurreko transposizioetatik bat kendu dugu, 11-6; beraz, orain 57 transposizio daude, hasierako posizioan bezala.

Merkatuan dauden buru-hausgarri batzuetan piezak ezin dira markotik altxatu. Beraz, zorizko posizio bat lortzeko piezak begiratu gabe mugitu behar dira marko barruan. Kasu horretan, zorizko posizio guztiek soluzioa dute, nahikoa izango da piezak desordenatzeko egin diren mugimenduak atzera egitea.

Markoan dauden karratu kopuruak eman zion izena, 15 buru-hausgarria, baina 16 buru-hausgarri ere dei dakioke, guztira hamasei karratu sartzen direlako. Antzeko izenak erabiltzen dira 15 buru-hausgarriaren tamaina-aldaera desberdinetarako, hala nola 3×3 marko batean 8 karratu dituen 8 buru-hausgarria.

Buru-hausgarria mota honen ebazpenak lotura handia du matematikarekin. n buru-hausgarriena heuristikoak erabiltzen dituzten algoritmoak modelatzeko problema klasiko bat da. Bestalde, Richard M. Wilson-ek (1974) 15 buru-hausgarritik grafo finitu arbitrarioetara orokortzea aztertu zuen, jatorrizko puzzlea 4×4 sare-grafo bat izanik. Talde-teorian, 15 buru-hausgarriaren konbinazioak 3-zikloen bidez sor daitezkeenez, froga daiteke 15 buru-hausgarria A15 talde alternatuaren bidez adieraz daitekeela. Eta konputazioaren ikuspuntutik, n buru-hausgarrien bertsio handietarako soluzio bat aurkitzea erraza da, baina soluziorik laburrena aurkitzeko problema NP-zaila da.

Oinarrizko buru-hausgarriaren aldaera on bat da piezak lerratzea errenkada guztien batura eta zutabe guztien batura eta diagonalen batura 30 izan dadin, hau da, karratu magiko bat lortzeko.