Argazkilaria: François Haffner.
Joko hau Piet Hein matematikari eta poeta daniarrak asmatu zuen eta 1942an aurkeztu zuen Niels Bohr Institutuan. Geroago, Heinek con-tac-tix izenarekin berrizendatu zion arren, Danimarkan polygon izenarekin ezagutarazi zen, 1942ko abenduaren 26an Danimarkako Politiken egunkarian argitaratutako artikulu baten ondorioz.
John Nash matematikariak aldarrikatu zuen berak sortu zuela jokoa independenteki, 1948an edo 1949an Princeton-eko Unibertsitatean. Baina hori ez dago argi, ikertzaile daniarrek hex jokoan aritu zirelako unibertsitate horretan garai hartan. Martin Gardner-en arabera, Nash-en jarratzaileek Nash edo John deitu zioten jokoari, eta azken izen horrekin esan zuten jokoa bainu-baldosa hexagonaletan joka zitekeela.
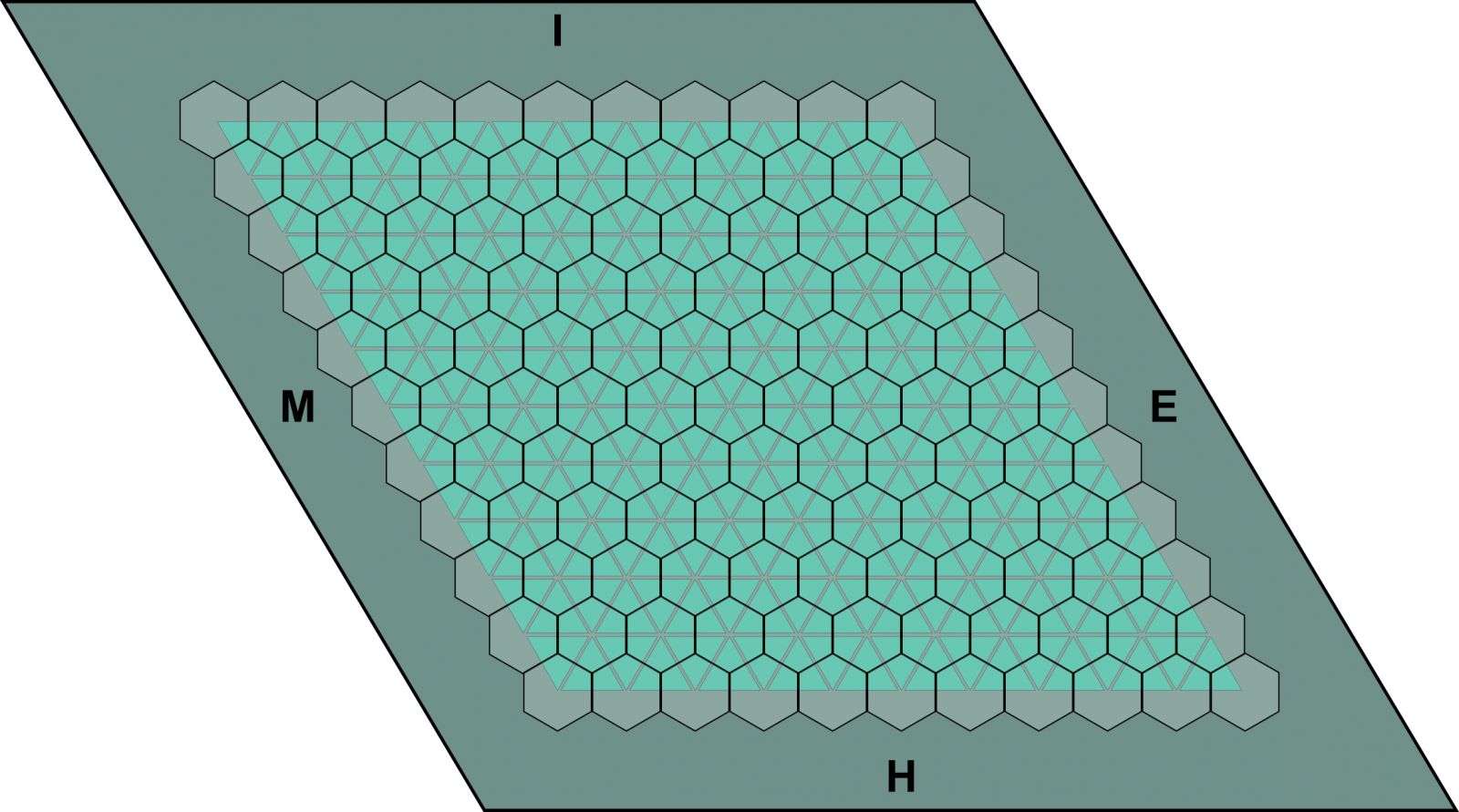
Hasiera batean, 1942an, Heinek jokoa banatu zuen, orduan polygon izenekoa, 50 orriko jokoen blok moduan. Orri bakoitzak 11×11 taula huts bat zuen, eta arkatz edo lumekin jokatu zitekeen. Orri horietako taula triangelu aldekidez zegoen osatuta, 10×10 aldeko erronboa osatuz eta fitxak triangeluen erpinetan irudikatuz. 1952an, Parker Brothers-ek jokoaren hex izeneko bertsio bat merkaturatu zuen, eta izena grabatuta geratu zen. Parker Brothers-ek con-tac-tix izeneko bertsioa ere saldu zuen 1968an.
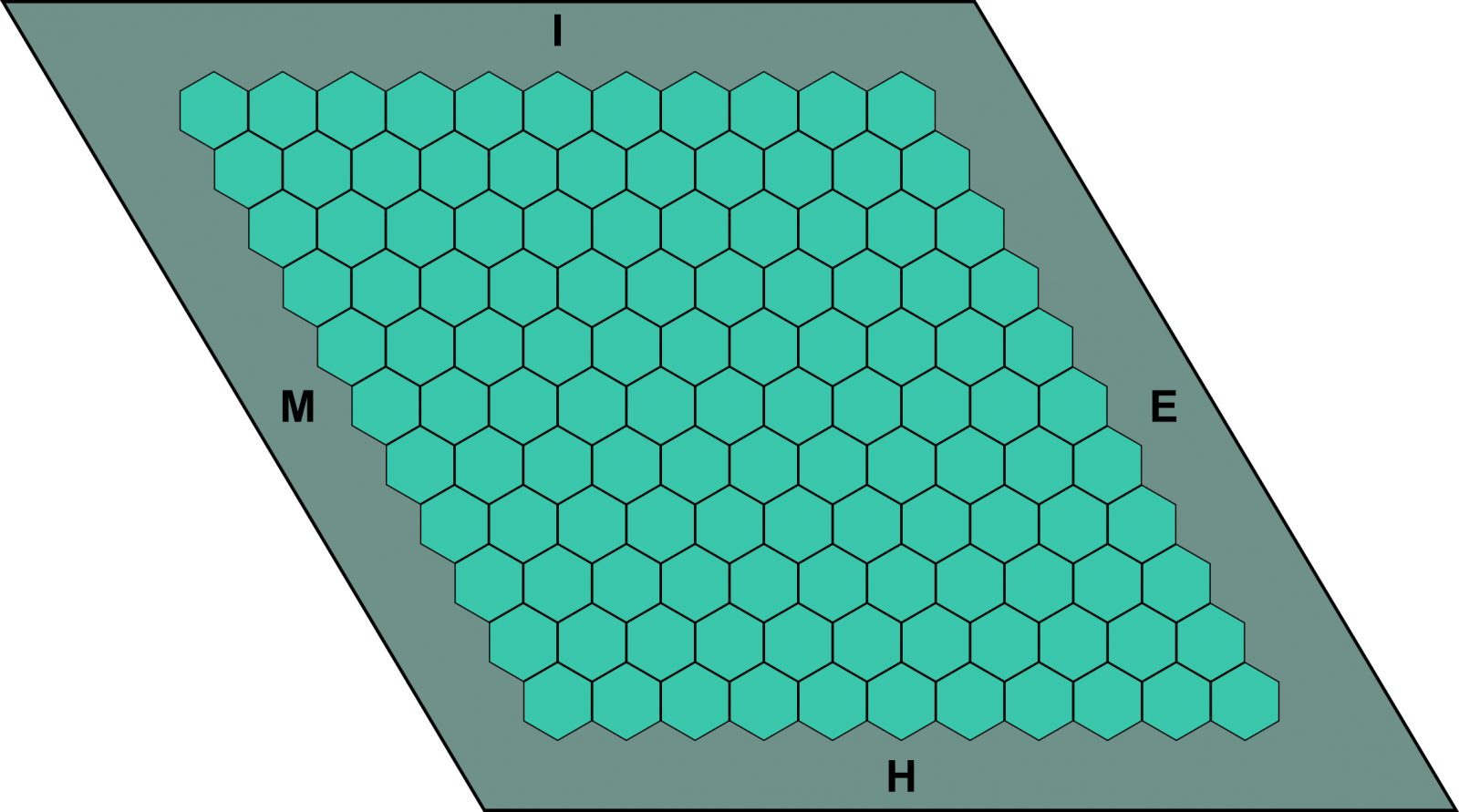
Gaur egun, hex jokoa taula baliokide batekin jokatzen da, triangeluen erpinetan hexagonoak jarrita. Hortaz, erronboaren alde bakoitzean 11 hexagono daude.
Hex jokoak berehala erakarri zituen matematikariak, irabazteko estrategiaren bila aritzeko.
Heinek bazekien 1942an hex jokoa ezin zela berdinketan amaitu; izan ere, jokoaren diseinurako irizpide bat bi jokalarietako batek bi aldeak konekta zitzakeela zen. Izan ere, erpin bakoitza hiru norabidek zeharkatzen dute, hau da, kopuru bakoitia. Heinek bazekien ere lehen jokalariak irabazteko estrategia teorikoa zuela.
1952an, Nashek lehen jokalariaren estrategia irabazlearen existentziaren froga bat idatzi zuen.
1964an, Alfred Lehman matematikariak erakutsi zuen hex ezin zela matroide bitar gisa irudikatu; beraz, ez zegoen estrategia irabazle jakin bat eskuratzea sare angeluzuzen erregular batean, beste joko batzuetarako bezala.
Anatole Beck, Michael Bleicher eta Donald Crowe-ren Excursion into Mathematics (Worth Publishers, 1969) laneko artikulu batean, Beckek hex jokoaren aldaera bat proposatu eta ebatzi zuen. Hori dela eta, Becken aldaera deitu zioten. Demagun lehen jokalariak bere lehen jokaldiaren aukera bigarren jokalariari uzten diola. Hala ere, lehen jokalariak beti irabaz dezake zentzuz jokatzen badu? Beckek artikulu horretan erakutsi zuen lehena izkina batean hasten bada, bigarrenak irabaziko duela lerro bereko alboko laukian jokatuz. Bleicherrek adierazi zuenez, horrek Becken aldaerari interes oro kendu zion.
1981ean, Stefan Reischek erakutsi zuen hex jokoa PSPACE-osoa dela. Hau da, jokoa ordenagailuan aztertzeko, sarreraren tamaina taularen aldeko n lauki bada, erabili behar den memoriaren kantitatea n-ren polinomio bat da.
2002an, lehen estrategia esplizitua deskribatu zen 7×7 taula batean (murrizketa motako estrategia).
2019. urtera arte, hobeto egon ziren gizakiak hobeto jokatzen zuten ordenagailuak baino, gutxienez 19×19 bezalako taula handietan; baina 2019ko urriaren 30ean, Mootwo programak onlineko LittleGolem-en Elo maila onena zuen gizakiaren aurka irabazi zuen, hainbat txapelketatan ere irabazia.
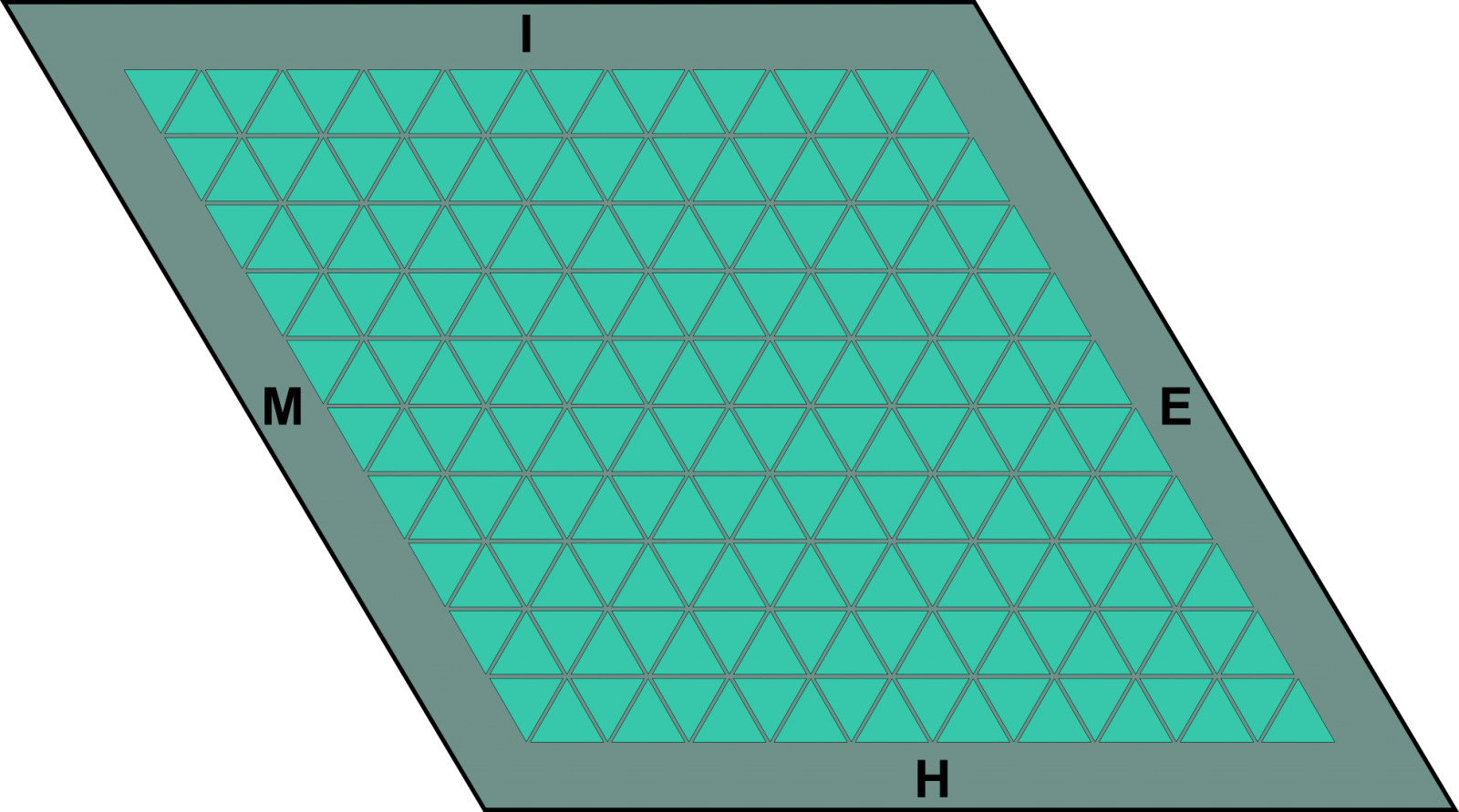
Osagaiak eta hasiera
Taula sare triangeluarra duen erronboa da. Bertan 121 bidegurutze daude (irudia).
Bi jokalarirentzako jokoa da.
Jokalariek 40na fitxa dauzkate, bi kolore. Jokalariek erronboaren aurrez aurreko bi alde aukeratzen dituzte. Erronboaren lau erpinak bi jokalariarenak dira.
Helburua, erronboaren elkarren aurkako bi alde fitxen lerro jarrai baten bidez lotzea da.
Arauak
Hasieran taula hutsik dago.
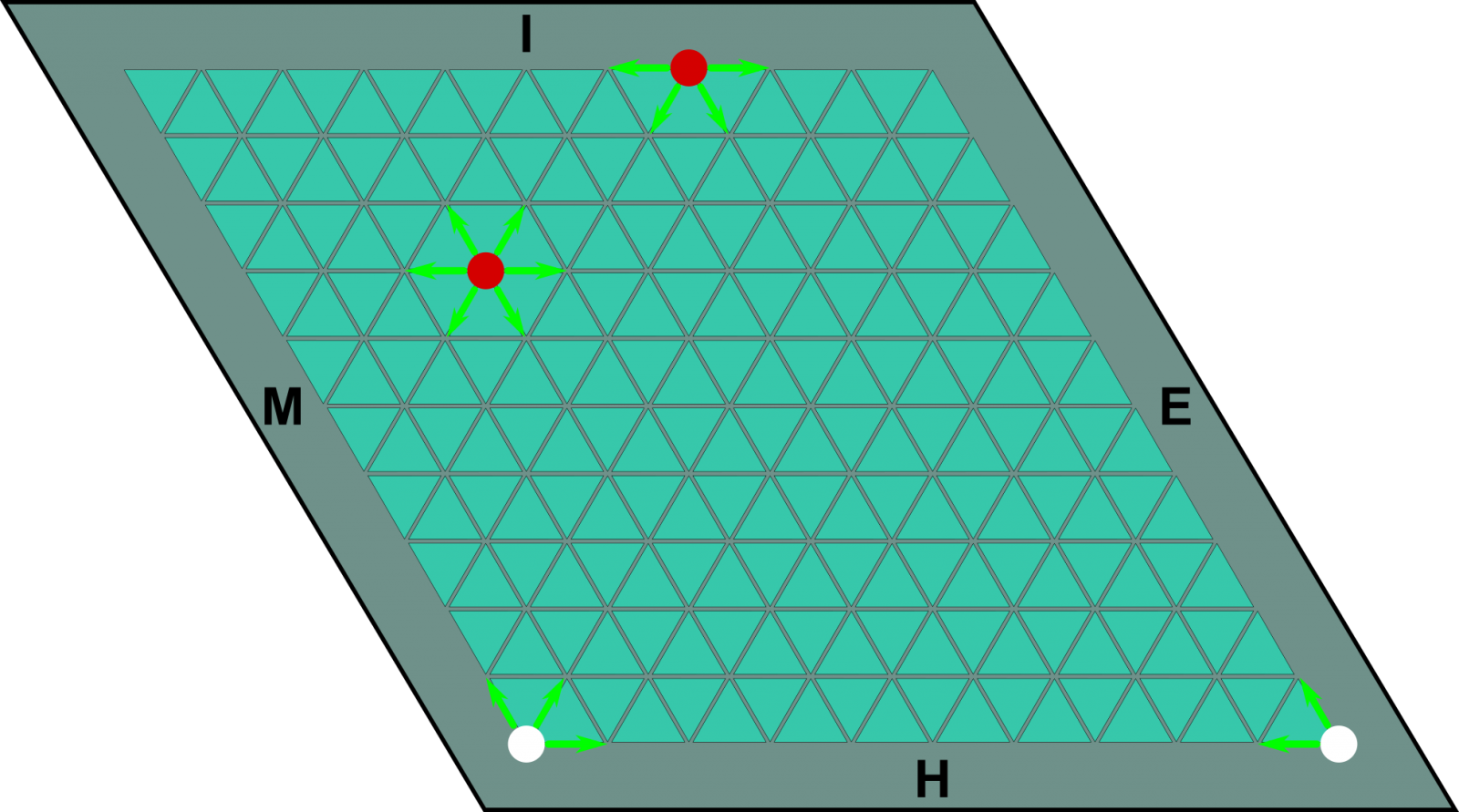
Hasi baino lehen, jokalari bakoitzak zein alde lotu behar dituen erabakiko da. Arau hau indarrik gabe utz daiteke (hots, jokalari bakoitzak nahi dituen elkarren aurkako aldeak lotuko ditu) eta ez du aurrez zeintzuk diren esango.
Fitxa beltzak dituena hasiko da eta, txandaka, fitxa bat jarriko dute taulako bidegurutze huts batean.
Jarritako fitxak ezin dira mugitu, ordeztu edo taulatik kendu.
Ondoz ondoko bi erpinetako bi fitxak kate berean daude.
Dagozkion bi aldeak fitxen kate batekin lehenbizi lotzen dituena izango da irabazlea.
Aldaera
Hemen ere pastelaren araua, batzuetan alde-aldaketaren erregela esaten zaiona, erabil daiteke. Bi jokalarientzako joko abstraktuetan maiz erabiltzen den araua da, joko horietan lehen jokalariak abantaila erabakigarria izan baitezake. Honela adieraz daiteke:
Lehen jokalariak lehenengo jokaldia egin ondoren, bigarren jokalariak aukera hauetako bat du:
- beste jokalariaren lehen jokaldia onartzea eta bigarren jokalaria izaten jarraitzea, hurrengo jokaldia egiteko, edo
- aldez aldatu, eta lehen jokalaria bihurtu. Lehen jokalariak egindako jokaldia beretzat hartuko du eta lehen jokalaria bigarrena bihurtuko da eta hurrengo jokaldia egingo du.
Pastelaren araua izena ideia honetatik dator: nola banatu bi pertsonek pastel bat berdintasunez eztabaidarik gabe; pertsona batek zatitzen du eta besteak erabakitzen du zer zatirekin geratzen den. Lehen jokalariak abantaila bat duen hex bezalako jokoetarako pentsatuta dago araua; adibidez, hex jokoan, lehen jokalariak beti irabaz baitezake. Horrela, lehen jokalariaren lehen jokaldia ez da oso ona izango, orduan abantaila handia emango bailioke bigarrenari, aldea aldatuko bailirateke, baina oso txarra ere ez da izango.