ikoMac
Percy Alexander MacMahon (1854-1926) matematikariak hainbat puzzle asmatu zituen eta, 1921ean, New Mathematical Pastimes (Denbora-pasa matematiko berriak) liburuan argitaratu zituen. Denbora-pasa horietako batean triangelu aldekide bat hartu zuen eta hiru triangelu isoszeletan banatu zuen, zentroa eta erpinak zuzenkiekin lotuz. Ondoren, lau kolore erabili zituen triangelu isoszeleak margotzeko, kolore bat errepikatzeko aukerarekin. Horrela, koloreen konbinazio guztiak sortu zituen, eta guztira hogeita lau triangelu desberdin lortu, planoko biraketak kontuan hartu gabe.
Triangelu horiekin, MacMahonek puzzle hau proposatu zuen: hexagono batean sartu behar ziren triangelu aldekideak, halako moldez non bi triangelu aldekideren ertzak elkartzen zirenean kolore berekoak izan behar zuten eta, horrez gain, hexagonoko perimetroan geratzen ziren triangelu isoszeleek kolore bera izan behar zuten. Hexagonoaren aldea triangelu aldekideen aldearen bikoitza zen.
2018an, José Luis Martín Montaño-k Triángulos de MacMahon, del plano al espacio (MacMahonen triangeluak, planotik espaziora) artikulua idatzi zuen Suma aldizkariaren 87. zenbakian, 41-48 orr. Bertan, Martínek MacMahonen triangeluak planotik ikosaedro batera eraman zituen puzzle hau proposatuz: ikosaedroan MacMahonen hogei triangelu jarri behar ziren, halako moldez non bi triangeluren ertzak elkartzen zirenean kolore berekoak izan behar zuten. IkoMac puzzlea jaio zen.
IkoMac-en garapena ikus daiteke Martínen Geogebrako MacMahonen ikosaedroa orrian.
Osagaiak
MacMahonen ikosaedroak edo IkoMac-ek osagai hauek ditu:
- Ikosaedro (aurpegietan hogei triangelu aldekide dituen poliedro erregularra) itxurako taula.
- MacMahonen hogeita lau triangeluak.
Arauak
Bakar-jokoa
Hogeita lau triangelu aldekideetatik hogei hartu behar dira eta ikosaedroan jarri behar dira, halako moldez non bi triangeluren ertzak elkartzen direnean kolore berekoak izan behar duten
Estrategia
Argi izan behar dugu ikosaedroa osatzeko ez ditugula triangeluak zoriz aukeratu behar.
Kontuan hartu behar dugu baztertzen diren triangelu isoszeleetan, kolore bakoitzeko triangelu isoszeleen kopuruak bikoitia izan behar duela.
Ikosaedroa betetzeko, lau triangelu aldekide baztertu behar ditugu, hau da, hamabi triangelu isoszele. Lau triangelu aldekide ezabatzeko, sei aukera daude, eta honela multzokatu daitezke, kolore bakoitzeko triangelu isoszeleen kopuruaren arabera:
I. taldea: kolore bateko zortzi triangelu, beste kolore bateko bi triangelu eta hirugarren kolore bateko beste bi triangelu. Adibidez:
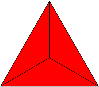
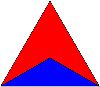
II. taldea: kolore bateko sei triangelu eta beste kolore bateko sei triangelu. Adibidez:
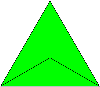
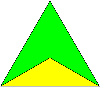
III. taldea: kolore bateko sei triangelu, beste kolore bateko lau triangelu eta hirugarren kolore bateko beste bi triangelu. Adibidez:
IV. taldea: kolore bateko sei triangelu eta, gainerako hiru koloreetatik, bina triangelu. Adibidez:
V. taldea: hiru koloretatik launa triangelu. Adibidez:
VI. taldea: bi koloretatik launa triangelu eta, gainerako bi koloreetatik, bina triangelu. Adibidez:
Talde guztiek soluzioren bat ematen dute.
Jokoa
Bi, hiru edo lau jokalarirentzako jokoa da.
Bi eratara joka daiteke. Aurretik puntuazio bat finkatzen da eta, hori lortzeko, behar diren partidak jokatzen dira. Edo, aurretik partida kopurua finkatzen da eta puntu gehien lortu beha da.
Partida hasieran, triangeluak ahoz behera jartzen dira mahaian, nahasten dira eta jokalarien artean banatzen dira edo jokalariek zoriz hartzen dituzte.
Triangelu aldekide gorria duena hasiko da. Hurrengo partidan, eskuineko jokalaria hasiko da, eta horrela partida guztiak jokatu arte. Lehenengoan izan ezik, gainerako partidetan nahi den triangeluarekin has daiteke.
Lehenengo jokalariak triangelua jarriko du ikosaedroan. Txanda ezkerretik eskuinera igaroko da. Horrela, hurrengo jokalariak, aurrekoaren eskuinekoak, beste triangelu bat jarriko du bi baldintza betez:
jartzen duen triangelu berriak, gutxienez, jarritako triangelu baten ertz bat ukitu behar du eta
ukitzen dituen ertzen koloreekin bat etorri behar dute triangelu berriaren ertzen koloreek.
Irudian, mahaiko triangelu berde-gorri-urdina ikosaedroaren aurreko hutsunean jar daiteke, jarritako bi triangelu ukitzen dituelako eta alde komunen koloreak bat datozelako, berdea berdearekin eta dorria gorriarekin.
Txanda duen jokalariak aukera du, bere triangelua jarri baino lehen, ikosaedroan jarrita dagoen triangelu bat mugitzeko, beti ere aurreko bi baldintzak betez. Ondoren, bere triangelua jarriko du.
Jokalari batek ezin badu bere triangelurik jarri, txanda hurrengo jokalariari igaroko dio.
Partida bukatuko da
1. jokalari batek ikosaedroa osatzen duenean bere triangelu batekin, edo
2. jokalari batek bere azken triangelua jartzen duenean, edo
3. jokalariek ezin dutenean triangelu gehiagorik jarri.
Lehenengo kasuan, jokalariak 10 puntu lortuko ditu.
Bigarren kasuan, bukatu duen jokalariak jarri gabe geratu diren triangeluak adina puntu jasoko ditu.
Hirugarren kasuan, triangelu gutxien dituen jokalariak gainerako jokalariek dituzten triangeluak adina puntu jasoko ditu. Bi jokalarik berdintzen badute, bakoitzak jasoko dituen puntuak zenbatzeko, berdindutakoaren triangeluak ere hartuko dira kontuan.