Osagaiak eta hasiera

Lau kubo daude eta bakoitzak sei aurpegiak lau kolore desberdinekin margoturik ditu.

Bakar-jokoaren helburua lau kuboak zutabe batean pilatzea da, zutabearen lau aurpegietan lau koloreak ikus daitezen.

 

Arauak

Kuboak bata bestearen gainean pilatu behar dira, aldeko aurpegietan kolore desberdinak agerian gera daitezen.

 

Lau kubo jokoa

Hauek dira lau kuboen planoko garapenak:

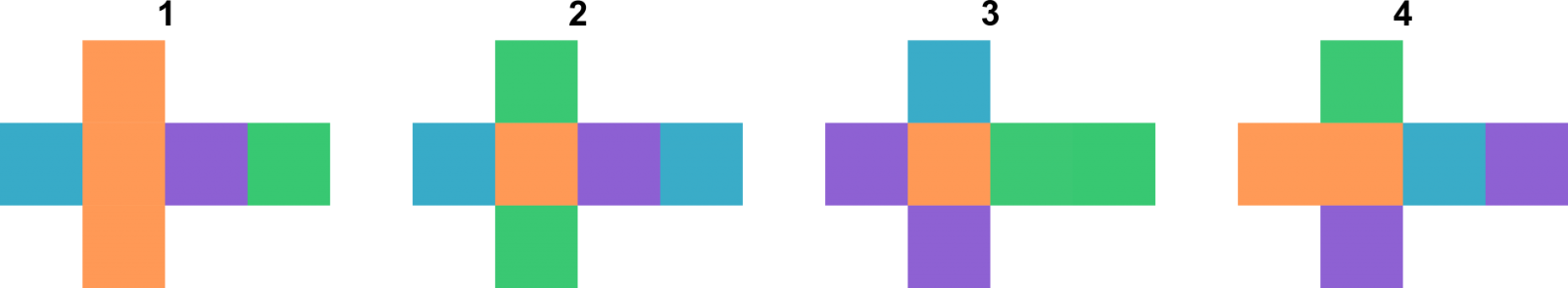
Lau kubo jokoaren soluzioa

Kubo baten sei aurpegiak kolore batez margotzen dira: berdea (B), laranja (L), morea (M) eta urdina (U). Jokoaren helburua kuboak lauko zutabe batean jartzea da, zutabearen lau aurpegietan lau koloreak (desberdinak) ager daitezen. Har ditzagun goiko irudiko kuboak, erakusten den bezala zenbakituak. (Kubo horiek joko honen adibide bat besterik ez dira. Beherago beste bi adibide daude.) Lehenik, antolaketa posibleen kopurua zenbatetsi behar da. 1 kuboa zutabearen behealdean jarri nahi badugu, gehienez hiru modu daude horretarako. Goiko irudian 1 kuboa garatu dugu, eta ikusten dugu ez dagoela alderik aurpegi morea edo aurpegi urdina mahaiaren gainean jartzen badugu. Gainerako lau aurpegiak baino ez zaizkigu interesatzen, zutabearen oinarrian. Kontrako hiru aurpegi-bikoterekin, lehenengo kuboa zutabearen oinarri gisa jartzeko hiru modu egongo dira gehienez. Orain, har dezagun 2 kuboa. Kolore batzuk errepikatzen diren arren, bigarren kuboa lehenengoaren gainean jartzeko sei modu daude. Orduan, bigarren kuboa biratu dezakegu, lehen kuboaren goiko aurpegia edo bigarren kuboaren beheko aurpegia aldatu gabe. Lau errotazio posiblerekin, bigarren kuboa lehenengoaren gainean 24 modutan jar dezakegu. Arrazoibide horrekin jarraituz gero, ikus dezakegu (3)(24)(24)(24) = 41.472 aukera daudela kontuan hartzeko. Eta agian ez dago soluziorik!

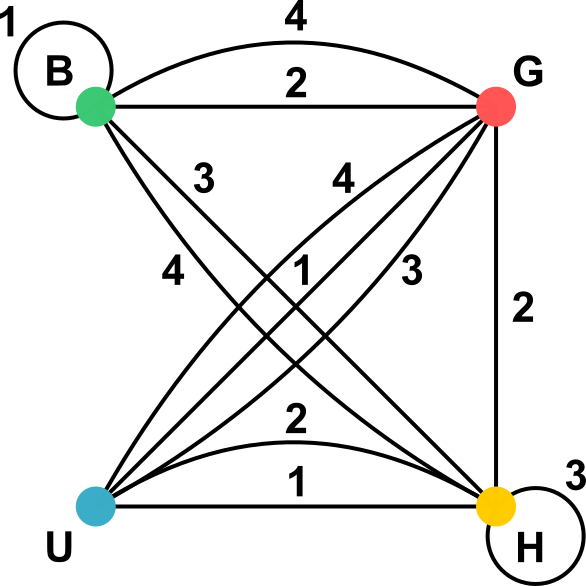
Buru-hausgarria ebazterakoan, konturatzen gara zaila dela kuboen kontrako aurpegien koloreen (1) eta koloretako zutabeen (2) erregistroak mantentzea. Grafo batek (berez, multigrafo etiketatu batek) egoera ikusten lagunduko digu. Eskuineko irudian, B, L, M eta U erpinak dituen grafo bat ageri da. Kubo bakoitza aztertzean, kontrako hiru aurpegi-bikoteak aztertuko ditugu. Adibidez, 1 kuboak kontrako bi aurpegi laranjaz margotuta ditu; beraz, L erpinean begizta bat  marrazten da eta 1 (lehen kuboarena) etiketa jartzen zaio. 1 ikurra duten irudiko beste bi ertzek kontrako aurpegi urdina eta morea eta kontrako aurpegi laranja eta berdea irudikatzen dituzte. Egin gauza bera beste kuboekin, irudiko grafoa lortzeko.

Grafotik abiatuta, ikusiko dugu 12 ertz daudela hiruko lau multzotan, kuboen etiketen arabera. Erpin bakoitzean biltzen diren ertzen kopuruak lau kuboetan kolore hori duten aurpegi kopurua adierazten du. (Begizta bi aldiz kontatuko dugu.) Beraz, eskuineko irudiak adierazten du lau kuboetan sei aurpegi berde, zazpi aurpegi laranja, sei aurpegi more eta bost aurpegi urdin daudela.

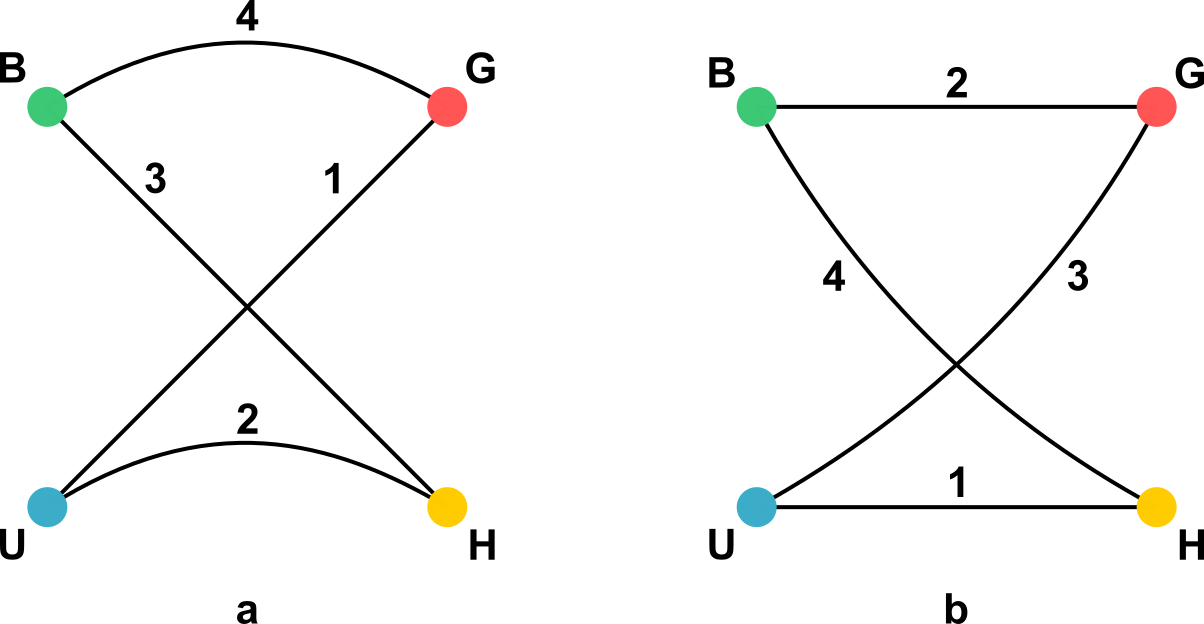
Zutabe batean lau kuboak pilatuta, zutabearen kontrako bi aurpegi aztertuko ditugu, aurrekoa eta atzekoa esaterako. Antolamendu horrek eskuineko grafoaren lau ertz ditu, non etiketa bakoitza behin bakarrik agertzen baita. Kolore bakoitza zutabearen aurpegi batean behin bakarrik agertuko denez, kolore bakoitzak bi aldiz agertu behar du lau ertz horien mutur gisa. Zutabearen beste bi aurpegietarako, ezkerrekoa eta eskuinekoa, emaitza bera lor badezakegu, asmakizuna ebatziko dugu. Ezkerreko (a) irudian ikus dezakegu zutabearen kontrako bi aurpegiek lau koloreak dituela, kuboak irudiko azpigrafoak emandako informazioaren arabera ordenatzen badira. Hala ere, zutabearen beste bi aurpegiek ere baldintza hori bete dezaten, (a) azpigrafoko ertzak erabiltzen ez dituen bigarren azpigrafoa behar da. Kasu honetan, badago bigarren azpigrafo bat, irudiko (b) azpigrafoan ageri den bezala.

4. irudian, kuboak kokatzeko modua agertzen da, 3. irudiko azpigrafoek adierazten duten moduan.

Oro har, lau kuboen kasuan, multigrafo etiketatu bat eraikiko dugu, eta bi azpigrafo aurkitzen saiatuko gara, baldintza hauek bete daitezen: (1) azpigrafo bakoitzak lau erpinak eta lau ertzak izan ditzan, bat etiketa bakoitzeko; (2) azpigrafo bakoitzean, erpin bakoitzean zehazki bi ertz bildu daitezela (begiztak bi aldiz kontatzen dira) eta (3) multigrafoaren ertz (etiketatu) bera ez dadila agertu bi azpigrafoetan.

 

 

Lau ero jokoa

Hauek dira lau eroen planoko garapenak:

Joko honekin hiru puzzle osa daitezke:

1. puzzlea: Atera fitxak kutxatik eta nahasi. Ondoren, sar itzazu kutxan, aurpegi bakoitzean 4 kolore lortzeko.

2. puzzlea: Atera fitxak kutxatik eta nahasi. 2×2×1 prisma bat osatu behar da, gaineko aurpegian lau kolore izateko; azpiko aurpegian ere lau koloreak izateko; eta aldeko aurpegi bakoitzean 2 kolore izateko.

3. puzzlea: Atera fitxak kutxatik eta nahasi. 2×2×1 prisma bat osatu behar da, gaineko aurpegian lau kolore izateko; azpiko aurpegian ere lau koloreak izateko; eta aldeko aurpegi bakoitzean kolore bakarra izateko.

 

Lau ero jokoaren 1. puzzlearen soluzioa

 

 

 

 

 

 

 

 

 

 

 

Lau dado jokoa

Hauek dira lau dadoen planoko garapenak:

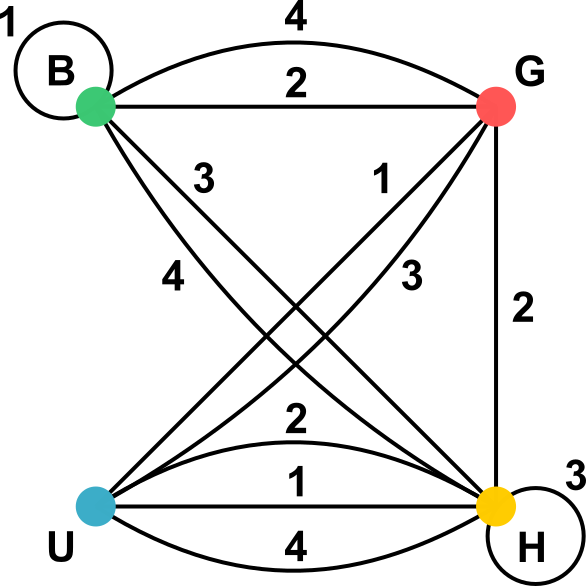
Joko honekin hiru puzzle osa daitezke:

1. Lau dadoak zutabe batean pilatzea da, zutabearen lau aurpegietan lau koloreak ikus daitezen.

2. lau dadoekin 2×2×1 prisma bat osatu behar da baldintza hauekin: lau dadoen gaineko aurpegietan kolore desberdinak agertzea, azpiko lau aurpegietan kolore bera agertzea, aldameneko bi aurpegietan kolore bera agertzea, eta prisma osoaren kontrako bi aurpegietan kolore bera agertzea.

3. lau dadoekin zutabe bat osatzea baldintza hauekin: aurpegi batek A kolorea izatea, beste aurpegi batek B kolorea izatea, hirugarren aurpegiak bi kubo C kolorekoak eta beste bi dado D kolorekoak, eta laugarren aurpegiak aurrekoaren koloreekin, baina beste ordena batean.

 

 

 

Lau dado jokoaren 1. puzzlearen soluzioa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

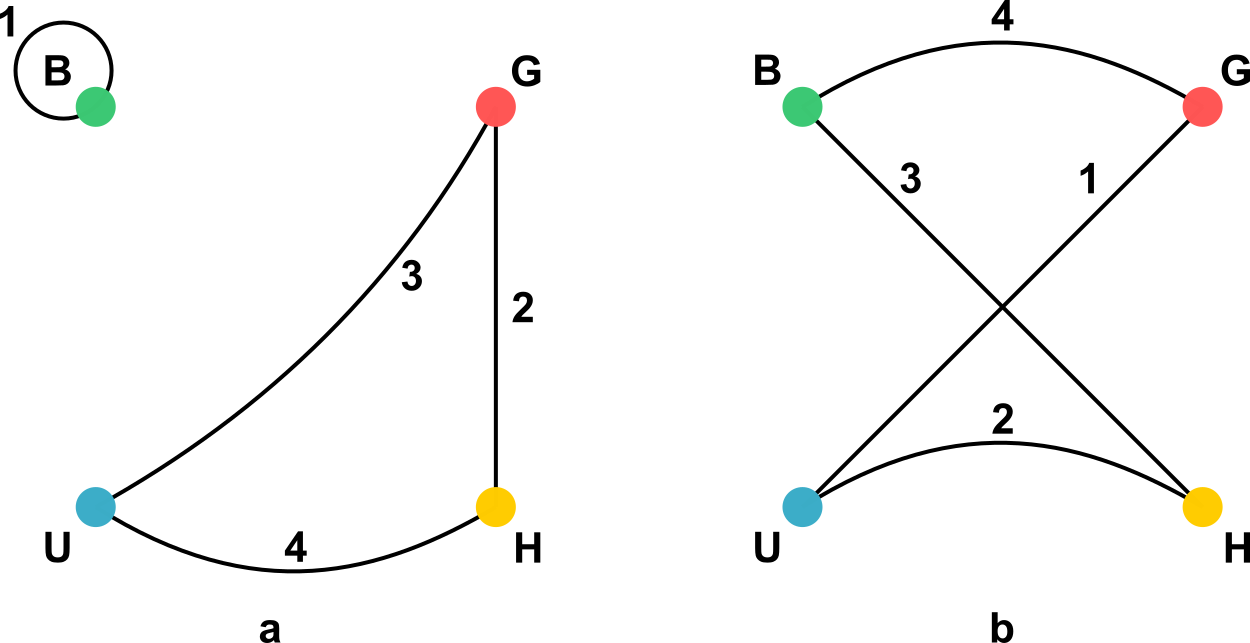
Iturriak

Ralph P. Grimaldi: Matemáticas Discreta y combinatoria. 3. ed. Addison-Wesley Iberoamericana, S.A., Wilmington, Delawere, AEB, 1997.

Jerry Slocum eta Jack Botermans: Puzzles, old & new. 1987.

Juegos de Ingenio (1). RBA, Bartzelona, 2003.

Eskuko arauak: Lagoon Games.

 

Wikipedia.en