pong hau k'i
Pong hau k’i Txinako Guangzhou eskualdeko joko baten izena da. Korean, joko berak on-moul-ko-no izena du; eta Thailandian sua tok tong izena. Indiako Punjaben, jokoak do-guti (bi joko) izena du.
Pong hau k'i blokeo-jokoa XIX. mendean dokumentatu zuen Stewart Culin-ek Ekialdeko Asian, baina Erdi Aroko graffitiek iradokitzen dute zaharragoa ere izan daitekeela.
Txinan, taula batean jokatzen diren jokoek k’i / qi izena daramate; Korean, diagrametan jokatzen diren jokoek, errota-jokoak bezala, ko-no izena daramate.
Harold James Ruthven Murray-k Gerra-jokoen artean Blokeo-jokoetan sartu zuen pong hau k’i, mū tōrere jokoarekin batera. Robert Charles Bell-ek Posizio-jokoen artean Blokeo-jokoetan sartu zuen, mū tōrere jokoarekin batera ere bai. Eta David Parlett-ek espazio-jokoen artean, Praktika murriztaileak dituzten jokoen artean sartu du, eta horrekin batera mū tōrere, L-jokoa eta pentaminoen jokoa. Pong hau k’i jokoa Taula-jokoa / Blokeo-jokoak atalean sailkatu dugu.
Joko honen izen komertzial bat chiangmai red sun da.
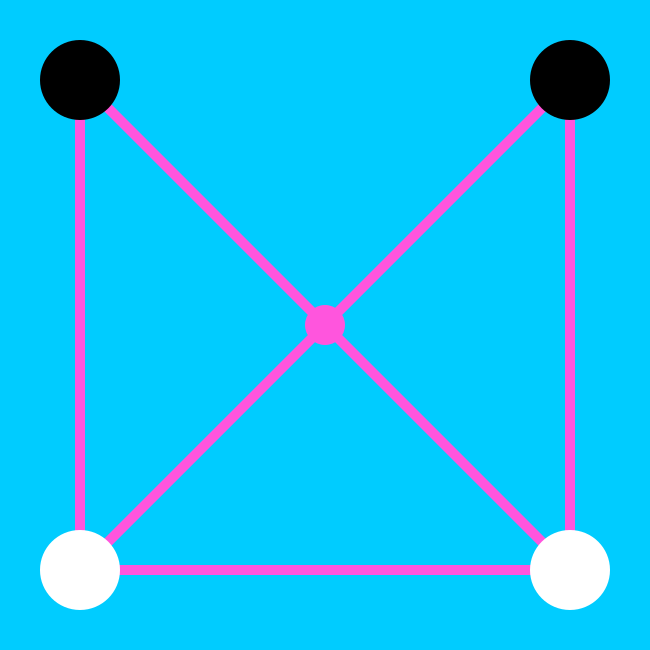
Osagaiak eta hasiera
Taula karratu batek, bi diagonalekin eta alde bat gabe, eta bost erpinek, kanpoko lauek eta diagonalen ebaki-puntuak, osatzen dute.
Bi jokalariek bina fitxa dituzte, beltzak eta zuriak.
Partidaren hasieran, fitxak karratuaren kanpoko lau erpinetan daude; jokalari baten bi fitxak falta den aldearen muturretan daude, eta bestearenak beste bietan.
Jokalariek aurkariaren bi fitxak blokeatu behar dituzte mugi ez daitezen.
Arauak
Zozketaz erabakiko da zein hasiko den, eta gero, txandaka arituko dira.
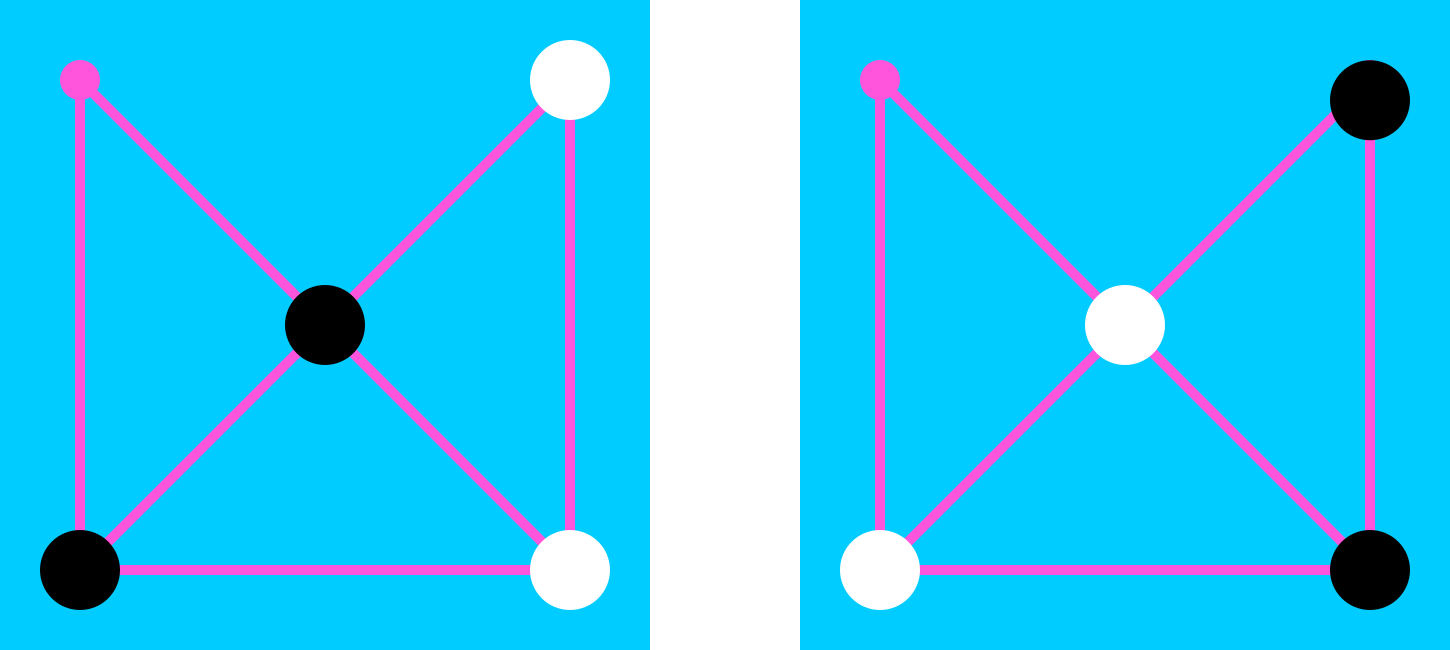
Lehenengo jokalariak fitxa bat mugituko du erpin batetik zentrora. Ondoren, bigarren jokalariak bere fitxa bat mugituko du libre geratu berri den erpinera. Horrela segituko dute txandaka fitxak mugitzen libre geratzen den posiziora.
Partida irabaziko du aurkariaren fitxak blokeatzea lortzen duen lehen jokalariak.
Aldaerak
Partidaren hasieran, taula hutsik dago eta jokalariak, txandaka, beren fitxak sartuko dituzte taulara. Fitxa guztiak sartu ondoren, fitxak mugitzen hasiko dira.
Chiangmai red sun bertsio komertzialak beste posizio bat proposatzen du jokoan hasteko: fitxak beltzak diagonal baten muturretan eta zuriak beste diagonalaren muturretan.
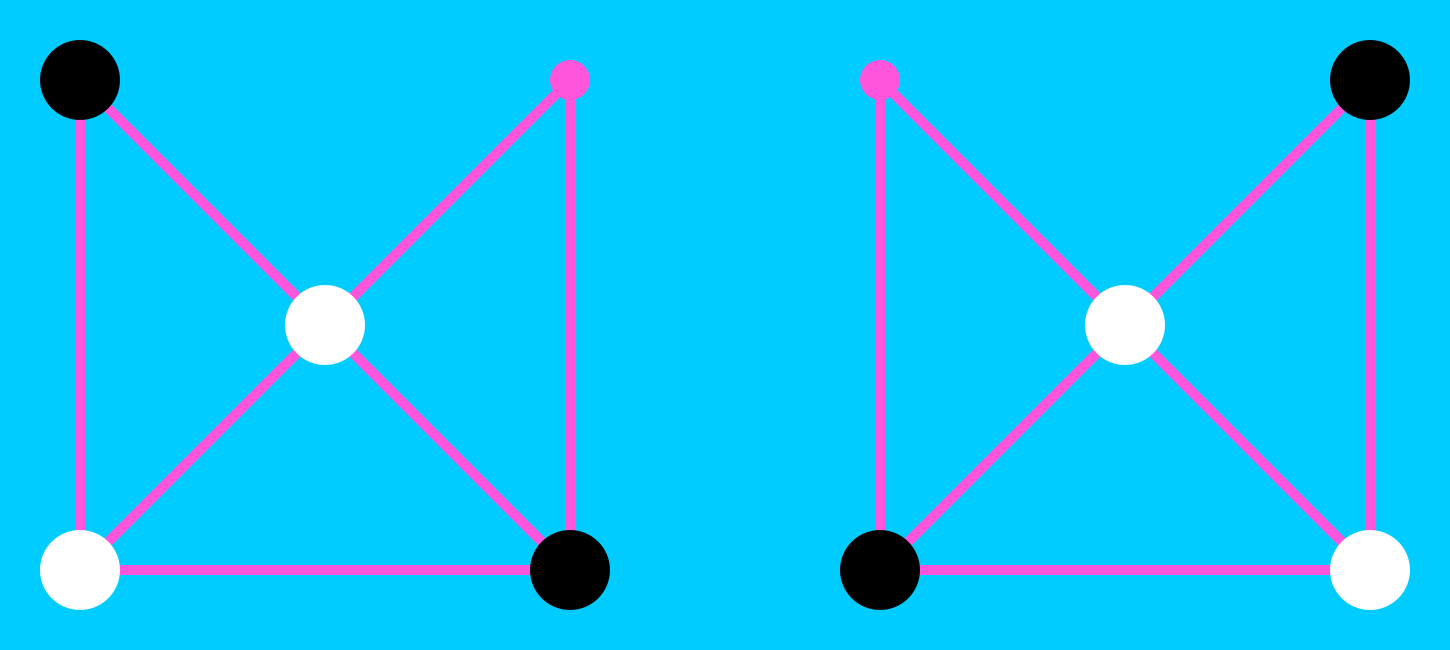
Bestelakoak
Joko-taula txiki honekin erraz kalkula daitezke jokoan zehar eman daitezkeen posizio guztien kopurua. Jokalariek bina fitxa berdin dituztenez, bi fitxa beltz, bi fitxa zuri eta posizio huts bat antolatu behar ditugu taulako bost posizioetan. Problema horrek errepikatuzko permutazioen formula behar du: 
Dena dela, posizio horietako asko elkarren simetrikoak dira, taulak simetria-ardatz bertikala duelako. Bi posizio auto-simetrikoak dira, hasierako bi posizioak hain zuzen (fitxa beltzak goian eta zuriak behean eta fitxa beltzak behean eta zuriak goian). Gainerako 28 posizioetatik 14 posizio beste 14 posizioen simetrikoak dira. Hortaz, esan daiteke 16 posizio desberdin daudela jokoan.
Posizioak adierazteko, taulako posizioak zenbakituko ditugu. Zentroari 3 egokitu diogu, taularen simetria posizioen adierazpenean islatzeko. Eta posizioak adierazteko, bost letrako hitzak erabiliko ditugu, B (beltza), Z (zuria) eta O (hutsik) letrekin. Hitzaren lehen letrak 1 posizioaren egoera adieraziko du: B fitxa beltza 1 posizioan badago, Z fitxa zuria 1 posizioan badago eta O 1 posizioa hutsik badago. Eta horrela beste lau letrekin. Esate baterako, hasierako posizio bat honela adieraziko dugu: BZOZB. Hasierako beste posizio bat hau da: ZBOBZ. Horiek dira, hain zuzen, auto-simetrikoak diren bi posizioak. Hona hemen hamasei posizio desberdinak:
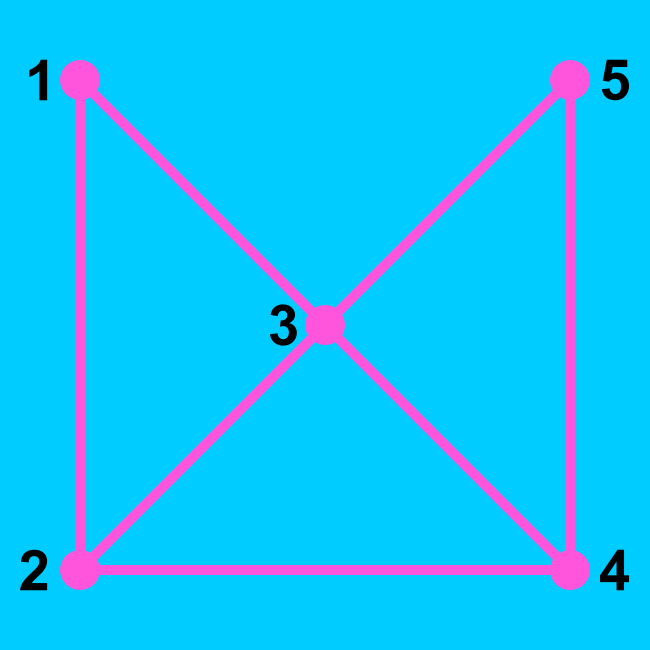
| 1 | BZOZB | 2 | OZBZB | 3 | ZOBZB | 4 | ZBOZB |
| 5 | OBZZB | 6 | BOZZB | 7 | OZBBZ | 8 | ZOBBZ |
| 9 | ZBOBZ | 10 | OBZBZ | 11 | BOZBZ | 12 | ZOZBB |
| 13 | OZZBB | 14 | BBOZZ | 15 | OBBZZ | 16 | BOBZZ |
Posizio simetrikoak lortzeko, nahikoa da taulako hitzak atzetik aurrera idaztea; esaterako, 6. posizioaren simetrikoa hau da: BZZOB. Ikus daitekeenez, 1. eta 9. posizioak, hasierako posizioak, auto-simetrikoak dira. Bestalde, 13. eta 15. posizioak zurien eta beltzen posizio irabazleak dira, hurrenez hurren. Azkenik, chiangmai red sun bertsio komertzialak 4. posizioa proposatzen du hasierako posizio gisa.
Hona hemen hamasei posizio desberdinen irudiak:
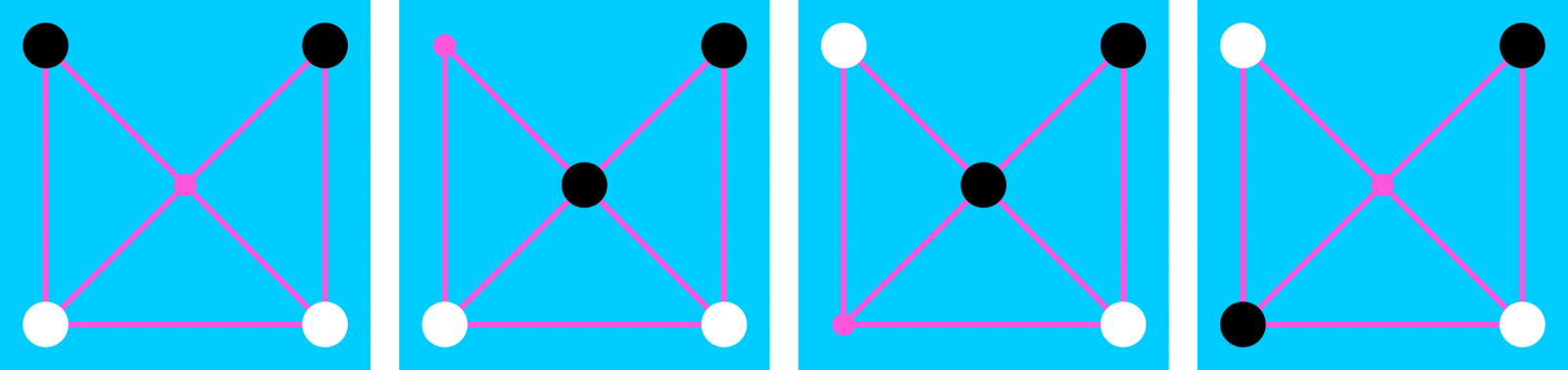
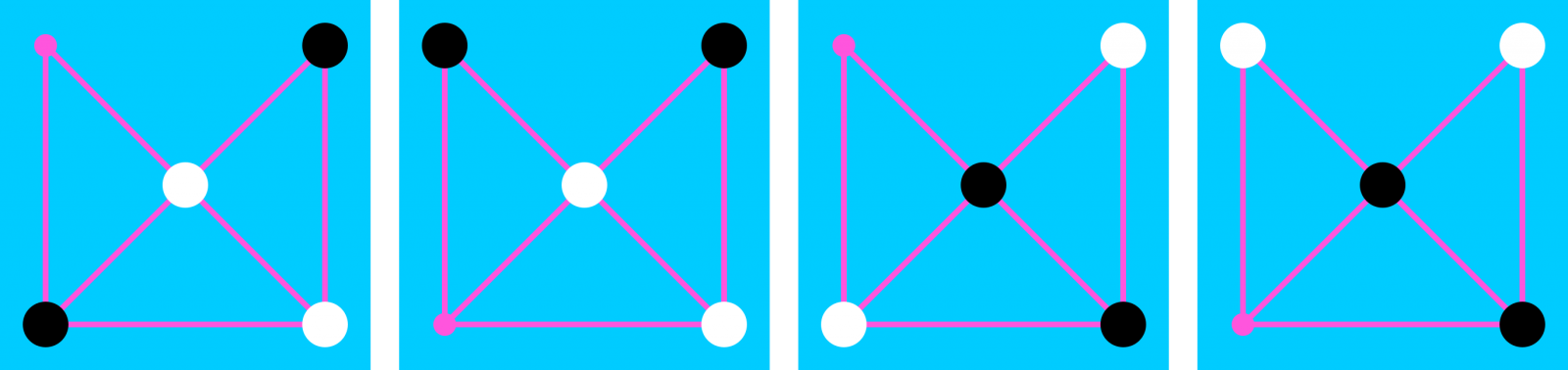
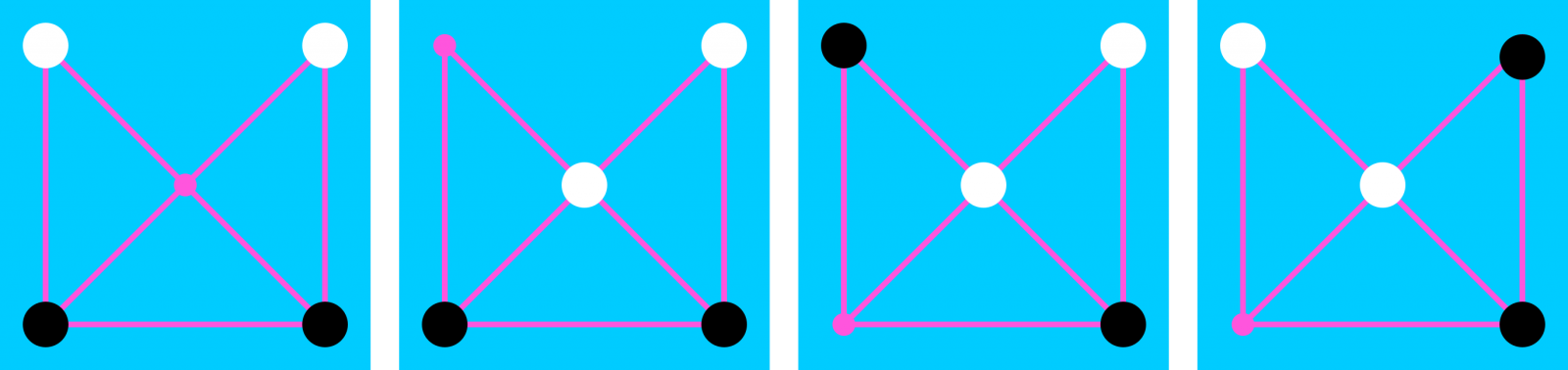
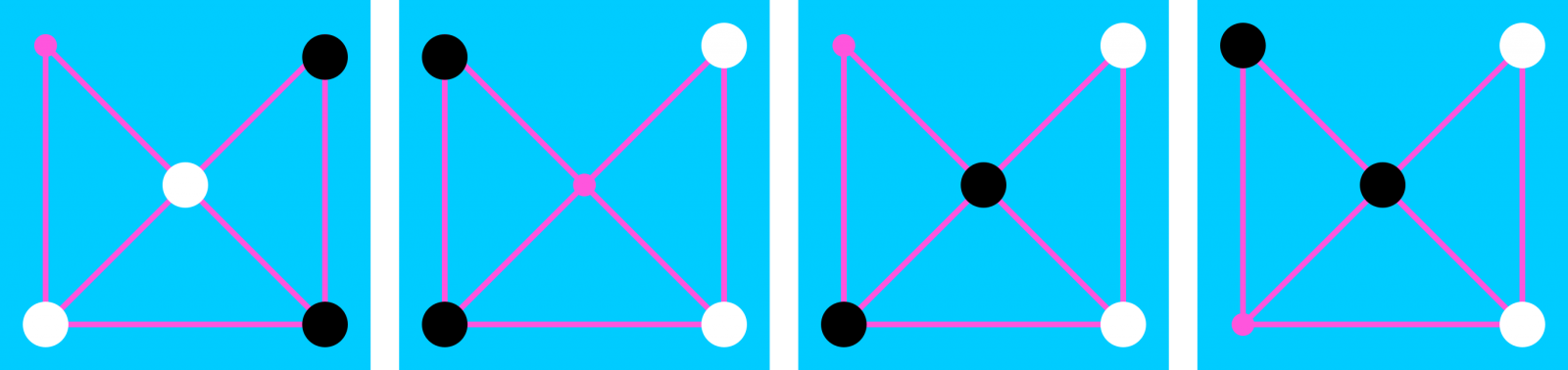
Iturriak
Robert Charles Bell: Board and Table Games from Many Civilizations, 2. Dover Publications, Inc., New York, 1979.
Robert Charles Bell eta Michael Cornelius: Juegos con Tablero y Fichas. Labor, Bartzelona, 1990.
Stewart Culin: Korean Games. Dover Publications, Inc., New York, 1895.
Harold James Ruthven Murray: A History of Board-Games other than Chess. Oxford University Press, Oxford, 1951.
David Parlett: History of Board Games. Echo Point Books & Media, Brattleboro, 1999.
Wikipedia (en)
Robin Evans: Pong Hau K’i. Games and Puzzles, 53. A H C Publications, 1976.
https://archive.org/details/sim_games-and-puzzles_1976-10_53/page/19/mode/1up?q=Evans
Antonio Javier Serrano Mora: Análisis matemático del juego llamado Pong Hau K'i, 2006.
http://olmo.pntic.mec.es/~aserra10/articulos/pong.html#CITEBell1990
Philip D. Straffin, Jr.: Position Graphs for Pong Hau K'i and Mu Torere. Mathematics Magazine, Bol. 68, 5 zk.. Mathematical Association of America, 1995.
https://www.jstor.org/stable/2690929?read-now=1&seq=1#page_scan_tab_contents