ritmomakia
Joko honen jatorria iluna da, baina Erdi Aroan sortu zen Europan. Ritmomakia hitzak zenbakien gudua esan nahi du latinez. Beste izen batzuk ere izan ditu: Ludus philosophorum, Filosofoen jokoa; 1910ean, jokoen historialari Jahn-ek zenbakizko xakea matematikarientzat izena jarri zion.
Ritmomakia sortu zenean, hainbat jokotan aritzen ziren Europan: dadoetan apustuekin aritzen ziren, xakea dagoeneko sartua zegoen Iberiar eta Italiar penintsuletatik, errota joko mota asko nonahi erabiliak ziren, eta taulak jokoa ere zabalduta zegoen.
Egile batzuek diote Pitagorasen zenbaki-teorian oinarritutako joko honen jatorria Bizantzion edo Alexandrian bilatu behar dela. Hala ere, ez dago aztarna fisikorik, ez eta idatzirik ere, hipotesi hori oinarritzeko.
Badira ritmomakia jokoa aipatzen duten XI., XII., eta XIII-XIV. mendeetako eskuizkribuak. Jokoa aipatzen duten iturri zaharrenetan, Arno Borst-en arabera, Asilo izeneko Würzburg-eko fraidearena da lehena, 1030 inguruan. Laster zabalduko da Erromatar-Germaniar Inperio Sainduan zehar eta 1040an agertuko da Hermannus Contractus (1013-1054) fraide jakitun eta matematikariaren testuan, Hermanni ritmomachia izenez ezagutzen da eta haren hiru eskuizkribu daude. Bigarrena, Accolytus beneditarrarena da, 1077an, eta Würzburg-eko monasterioan jokatzen zela dio. Ritmomaquia Wirceburgensis izenez da ezaguna eta haren zazpi eskuizkribu daude. Beste lan bat xi. mendeko Odonis ritmomaquia (1090), Odo izeneko fraide batena dela uste da eta bi kopia aurkitu dira. Eta azken iturri zaharra aipatzeagatik, Fortolfus fraidearen Fortolfi ritmomachia (1130) da, eta eskuizkribu bakarra du.
Iturri zaharrenak monasterioen testuinguruan kokatzen dira, non Boezioren Aritmetika azaltzen baitzen Quadriviumaren (aritmetika, geometria, musika eta astronomia) barnean. Gainera, ez Mendebaldeko Europan ez Ekialdeko Europan, ez dira holako idazkirik aurkitu. Hortaz, onargarria dirudi jokoaren jatorria testu zaharrak idatzi ziren Erdialdeko Europan kokatzea.
Aipatzekoa da testu zahar horiek ez dutela argibide handirik ematen jokoaren arauei buruz; izan ere, testu laburrak dira, azalpen ilunak eta piezen balioa ezaguntzat ematen dituzte, eta problema zehatzen soluzioak baino ez dute ematen. Badirudi adituei zuzenduak direla. Erdi Aroan asko jokatu zen, baina zenbakien progresioen ezagutza eskatzen zuenez, ikasien klasera murriztuko zen, segur aski. Hala eta guztiz ere, garai batean xakeak baino itzal handiagoa izan zuen.
Zeharkako aipamenei esker, badakigu ritmomakia jokoa helburu didaktikoekin erabili zela Boezioren Aritmetika ikasteko. Esaterako, XIII. mendeko Vetula poeman deskribatu eta goraipatzen da eta Tomas Morok, 1516ko Utopia lanean, jokoaren aldeko aipua egin zuen:
Afal ondo, ordu bat hartzen dute libertitzeko; udan, baratzean eta neguan, jangela handietan. Hor dira batzuk musikan ari eta besteak solasean elkarrekin. Zortea, eta beste horrelako joko zoro eta kaltegarriak ez dira aipu ere; bainan bi joko badituzte, nolazpait xake-jokoa iduriak: zenbaki-jokoa da bat eta zenbaki jakin batek bestea garaitzen du; bestea, gerla-jokoa da; eta bizioen eta bertuteen arteko gerla da gaia [1].
Aipatzen duen lehen jokoa, zortea, dadoak dira; eta zenbaki-jokoa ritmomakia da.
Testu horiek iradokitzen dute ritmomakia ongi ikusten zuela elizak buruko ariketa onuragarri gisa, xakea ez bezala. Ez dira erraz ulertzen bi jokaera horiek; ez bada xakean erregea hil behar zelako edo, akaso, xakea musulmanek ekarri zutelako Europara.
Ondoriozta dezakegu, beraz, jokoa XI. mendearen erdialdean sortu zela Alemaniako monasterioen esparruan; fraideen eskoletako ikasleak zenbakien aritmetikarekin trebatzeko helburua zuela. XI. eta XII. mendeetan Alemanian eta Frantzia aldean zabalduko zen eta XII-XIII. mendeetan Ingalaterrara igaro zen.
Inprenta asmatu arte ez zuen ritmomakiak monasterioen hormak gainditzea eta zabaltzea lortuko. Orduan, ritmomakiaren gidaliburuak ugaritu ziren. John Shirwood-ek 1482ko Liber de ludo arithmomachia lanean jokoa laburki deskribatu zuen. Jacques Lefèvre d’Étaples-en 1496ko Rithmimachie ludus qui pugna numerorum appellare Parisko unibertsitateko ikasleei zuzendua zen. Claude de Boissière-ren, 1554 eta 1556ko Le très excellent et ancien Jeu Pythagorique, dit Rithmomachie..., frantsesez eta latinez hurrenez hurren, garaiko gidaliburu xehatuena izan zen, ritmomakiaren erabilera zabaltzeko asmoz, arauak argiago azaldu zituelako. Alemanez idatzitako lehena Abraham Ries-en 1562ko Arithmomachia izan zen, monasterioetako testuetan oinarritua. William Fulke-ren eta Rafe Lever-en 1563ko The Most Noble Ancient, and Learned Playe, Called the Philosophers Game, Boissièreren liburuaren itzulpena, lan zabalduena izan zen Ingalaterran. Francesco Barozzi-ren 1572ko Il nobilissimo et antiquissimo Givocco Pythagorea nominato Rythmomachia cioe Battaglia de Consonantie de Numeri lanak zabalpen handia lortu zuen Erdialdeko Europan. Gustavus Selenus-en 1616ko Das Schach- oder Königsspiel liburuaren bukaeran Rythmomachia. Ein vortrefflich und uhraltes Spiel desz Pythagorae, Barozziren testuaren itzulpena, dator.
XVII. mendean ritmomakiaren entzutea gutxituko da. Matematikako ikasleen, ikasien edo jakintsuen jokoa izan zena halako batean desagertu zen. Esate baterako, Selenusen testuan xakeari buruzko liburuaren bukaeran agertzen da. Desagerpen horren arrazoi bat izan daiteke matematiketan eman ziren aldaketak, Boezioren aritmetika musulmanen aljebraz joan zen ordezkatzen pixkana. Unibertso ordenatu eta hierarkizatuak oinarri sendoa zuen Boezioren zenbaki-teorian; baina ikuspegi hori aldatzen hasi zen Errenazimentuarekin. Matematikaren irakaskuntzak bere ateak zabaldu zituen beste unibertso batzuk onartzeko.
Alemanian, XIX. mendean, Adler izeneko matematika-irakaslea eta xake-jokalaria ritmomakiaren alderdi hezitzaileak ateratzen saiatu zen, 1852ko eskola-programan, baina arrakastarik gabe. 1917an, Jahn matematika-irakaslea bere ikasleekin ere saiatu zen, baina ez zuen arreta handirik bereganatu.
XX. mendean ikerketa batzuk egin dira jokoaren jatorriaz eta arauaz. Bereziki, Alemanian egindako lan sakonek argitasun pixka bat eman diete bi alderdi horiei (Arno Borst, Detlef Illmer, Peter Mebben).
Theoni Pappas-ek, ritmomakian oinarriturik, Chase jokoa aurkeztu zuen haurrei zuzendutako 1997ko Math for Kids & Other People Too! liburuan. Chase jokoan piezek ez dute zenbakirik eta mugimenduetan jauziak onartuta daude.
[1] Tomas Moro. Utopia. 1516. Itzultzailea: Piarres Charritton, Klasikoak, Bilbo, 1992, 139. orr.
Ritmomakiaren osagaiak
Orain, ritmomakiaren osagaiez dauden zehaztugabetasunak ikusiko ditugu. Batzuetan egileen artean aldeak daudelako gertatzen dira, eta beste batzuetan gako batzuen inguruan daturik ez dagoelako.
Ritmomakia jokoaren taulari dagokionez, Boissièrek berak iradokitzen du aukera bat baino gehiago dagoela 8×16 laukiko laukizuzen bat erabiltzea proposatzen duenean, baina minimo gisa 10 laukiko luzera ematen duenean. Neurrietan 9, 12, 14 edo 16×8 aldaerak aipatzen dira testuetan. Taularen diseinuan, egile batzuek lauki zuriak eta beltzak erabiltzen dituzte, xakean bezala; beste batzuek kolore bakarra erabiltzen dute. Ez du ematen xake-itxurako taula behar denik.
Piezei dagokienez, egile guztiak bat datoz piezen balioetan eta dagokien forman. Piezen banaketa eta balioa hau da egile guztietan:
Jokalari batek 24 pieza argi hauek ditu: zirkuluetan, 2, 4, 6, 8 / 4, 16, 36, 64; triangeluetan, 6, 20, 42, 72 / 9, 25, 49, 81; karratuetan, 15, 45, 153 / 25, 81, 169, 289; eta piramidean, 91*.
Beste jokalariak 24 pieza ilun hauek ditu: zirkuluetan, 3, 5, 7, 9 / 9, 25, 49, 81; triangeluetan, 12, 30, 56, 90 / 16, 36, 64, 100; karratuetan, 28, 66, 120 / 49, 121, 225, 361; eta piramidean, 190*.
Piezen taulako kokapena, ordea, ez da beti bera egile guztietan. Esate baterako, Boissièrek piezak, nolabait, eskuinetik ezkerrera (8, 6, 4, 2 eta 9, 7, 5, 3) kokatu zituen taulan. Berozzik, ordea, Boissièrek emandako posizioaren simetrikoa eman zuen (2, 4, 6, 8 eta 3, 5, 7, 9).
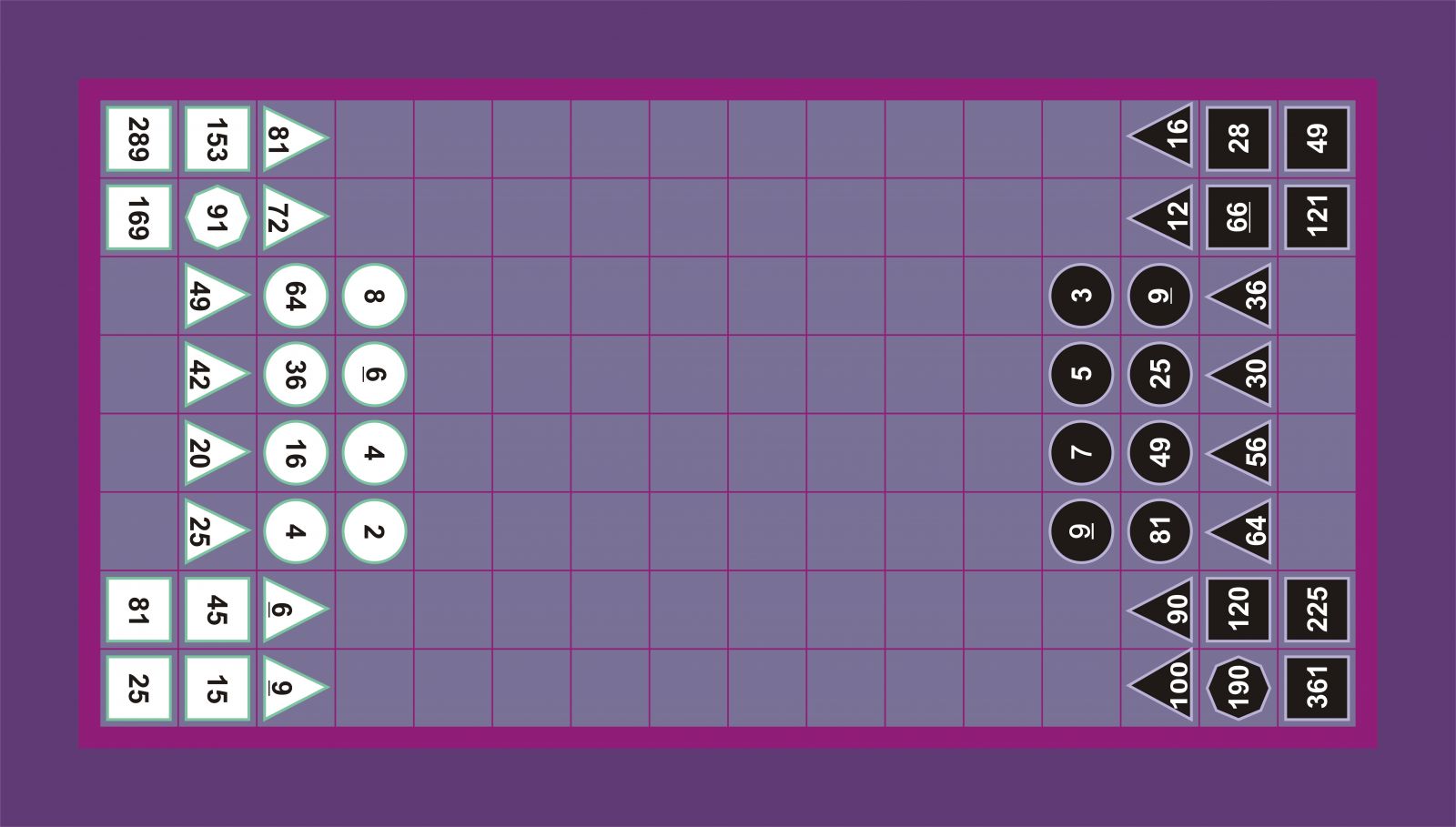
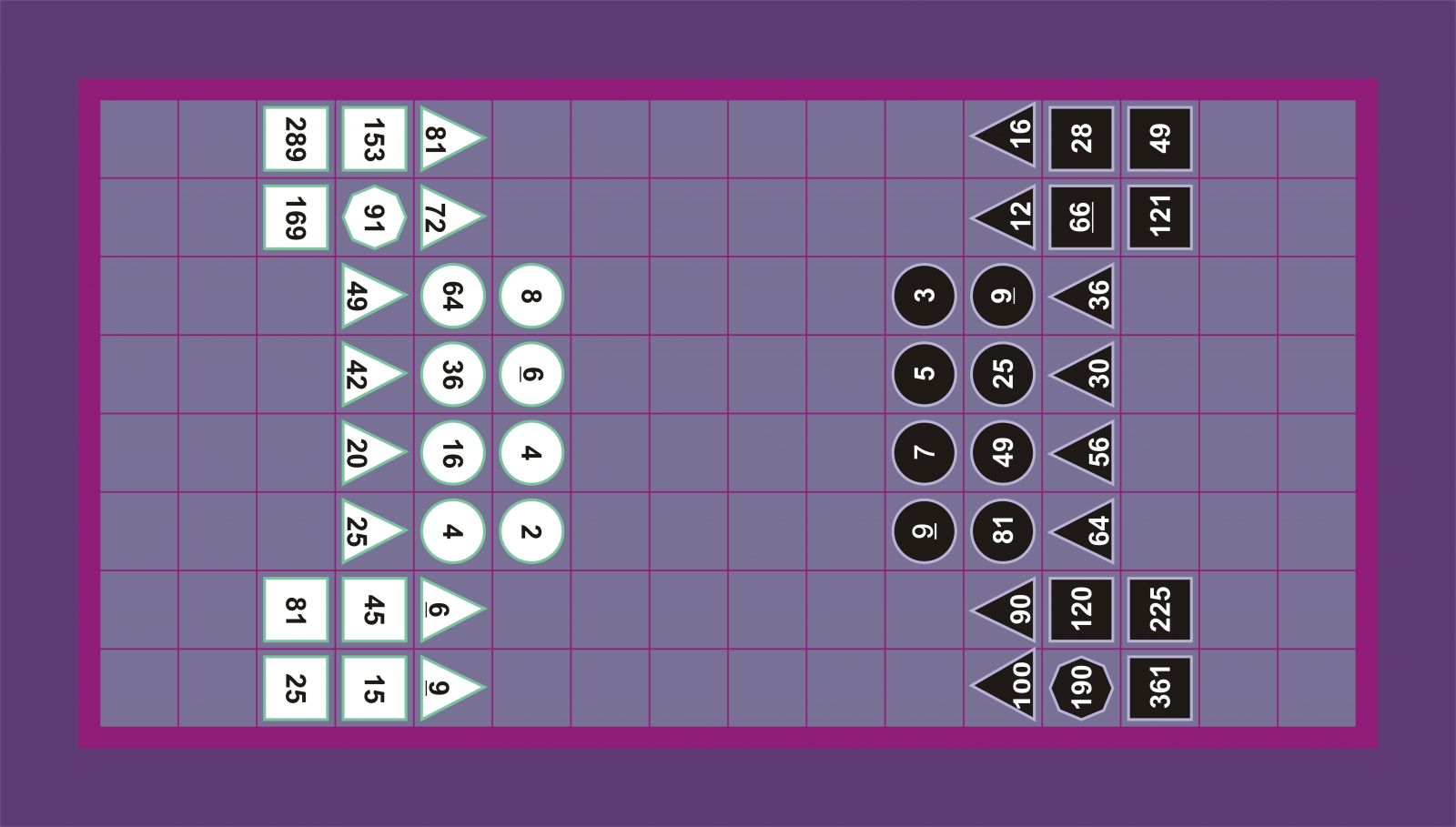
Boissière eta Fulke-Lever-3 Fulke-Lever-1
Hasierako beste posizio bat agertzen da Fulke-Lever-en testuan. Boissièrek ematen duen piezen posizio bera baina bi zutabe aurrerago erdialdera, bai bakoitiak bai bikoitiak.
Beste hirugarren batean, piezak falange moduan kokatuta daude 4×6 laukizuzen bat osatuz taularen alde motzen erdialdean. Badirudi antolaketa hori, ordea, zenbakien osaeratik eratortzen dela eta tarteko urrats gisa erabiltzen dutela Boissièrek eta Barozzik hasierako posiziora iristeko, eta ez hasierako posizio moduan. Berez, Barozzik azaltzen du nola kokatu behar diren piezak taulan lehenengo urratsean, hortik, gero, bigarren eta “perfetta” posiziora erraz pasatu ahal izateko.
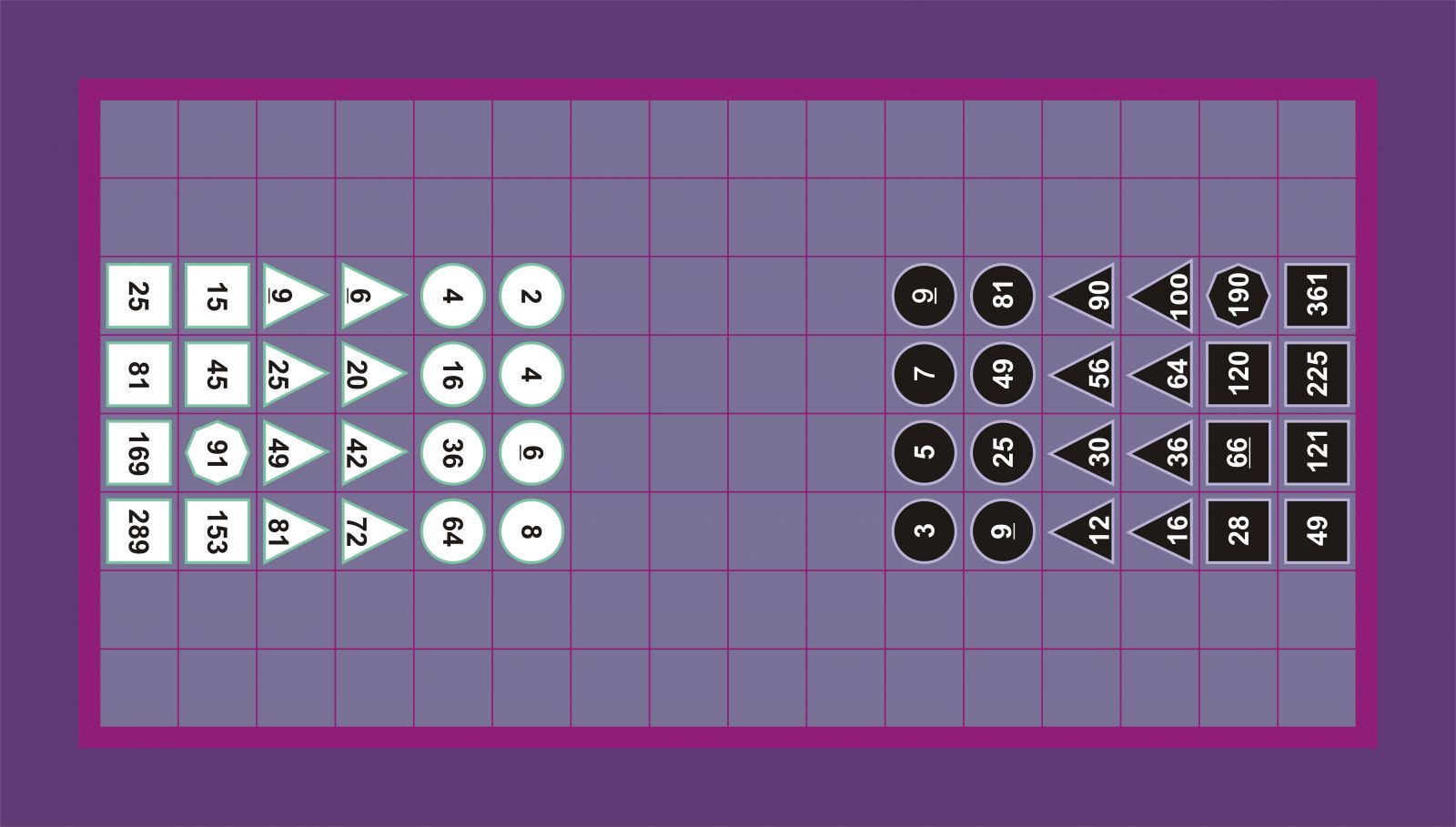
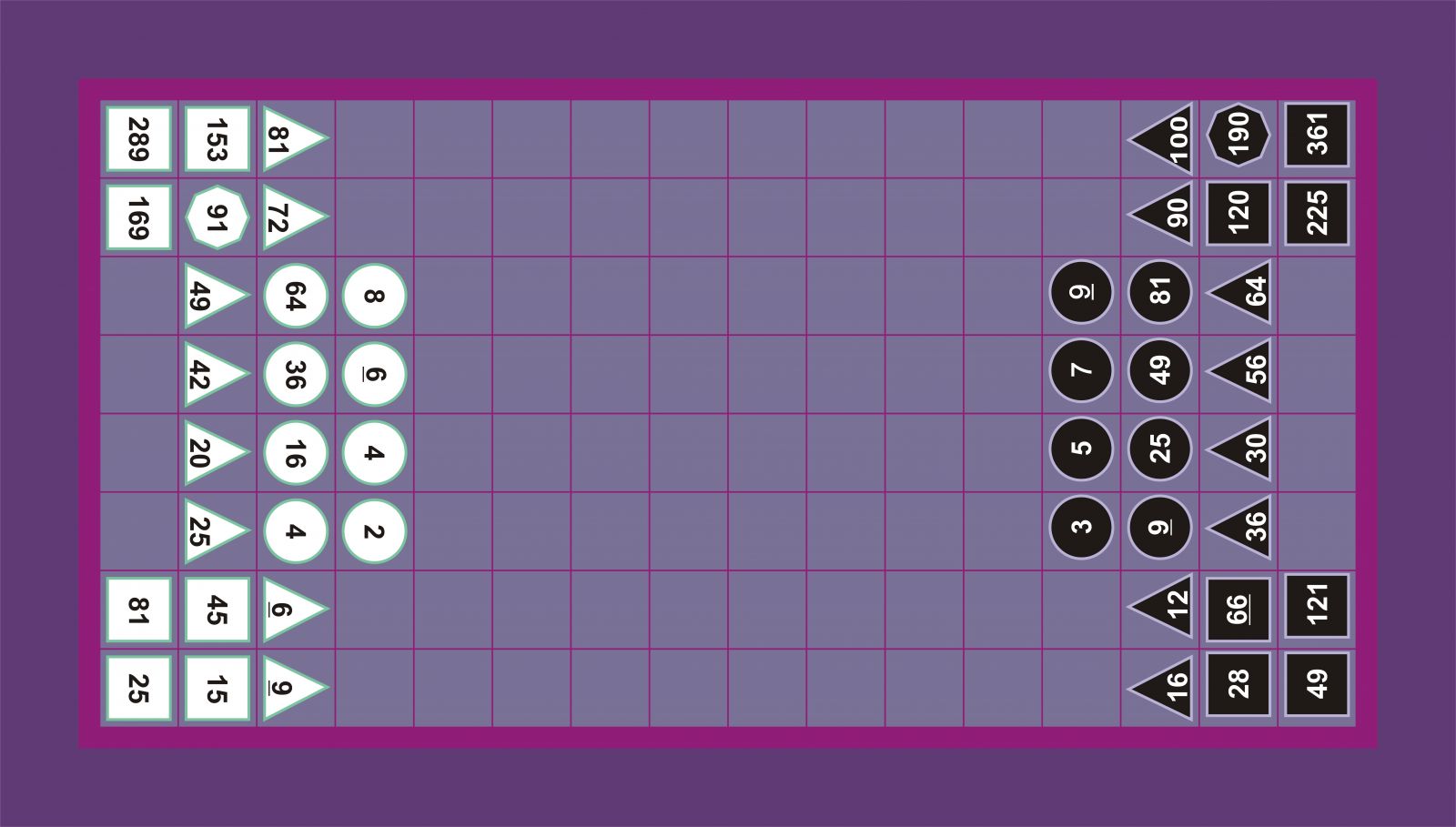
Boissière, Barozzi eta Fulke-Lever-2 Odo eta Stigter
Stigter-ek, bere aldetik, ezagutzen den diagrama zaharrenean (Odo-eranskina) oinarritzen da beste antolaketa bat emateko. Horren berezitasuna da pieza argiak eta ilunak simetriaz kokatzen dituela, xakean bezala, eta, ondorioz, piramideak taularen alde berean daude. Esaterako, 3ko iluna 2ko argiaren aurrean, 5eko iluna 4ko argiaren aurrean, etab.
Ritmomakiaren arauak
Arauei dagokienez, iturriak ez datoz bat ritmomakiaren arauak ematerakoan; areago, iturri batzuek aukera bat baino gehiago ematen dute. Piezen mugimenduen gutxienez hiru bertsio ikusi ditugu. Guk hemen Núñezen testuari, beraz Boissièreren testuari, jarraituko diogu.
Núñezek dio beti hasiko dela pieza argiak, bikoitiak, dituen jokalaria, hasieran konbinazioak osatzeko beltzek, bakoitiek, duten abantailatxoa orekatzeko. Mebben-ek dio, ordea, ilunak, bakoitiak, hasten direla, argiek aukera gehiago dutelako harrapatzeko eta harmoniak osatzeko. Cazaux-Knowltonek diote testu gehienek pieza ilunak, bakoitiak, hasten direla zehazten dutela.
Mugimenduak
Egileak ados daude, esplizituki edo inplizituki, esatean bi pieza ezin direla lauki berean egon; baina, jauziei dagokienez, irizpide desberdinak daude.
Mugimenduen irismena aipatzen dugunean, kontuan izan behar dugu Erdi Aroan pieza bat 4 lauki mugitzen zela esaten zutenean, 4 kopuru horren barnean sartzen zirela abiatzeko laukia eta iristeko laukia. Guk gaur egun pieza bat 3 lauki mugitzen dela esango genuke, abiatzeko laukia kontuan hartu gabe, eta horrela emango ditugu mugimenduen irismenak testu honetan.
Boissièreri jarraituz, zirkuluak ortogonalki mugi daitezke, aurrera-atzera edo ezker-eskuin, alboko lauki huts batera, baina ez diagonalean. Triangeluak diagonalean zehazki bi lauki mugi daitezke, bidea zein bigarren laukia hutsik egonez gero. Karratuak edozein norabidetan zehazki hiru lauki mugi daitezke, bidea zein hirugarren laukia hutsik egonez gero. Aldaera hori bera ematen dute Barozzik, Selenusek eta katalanezko wikipediak [[1]].
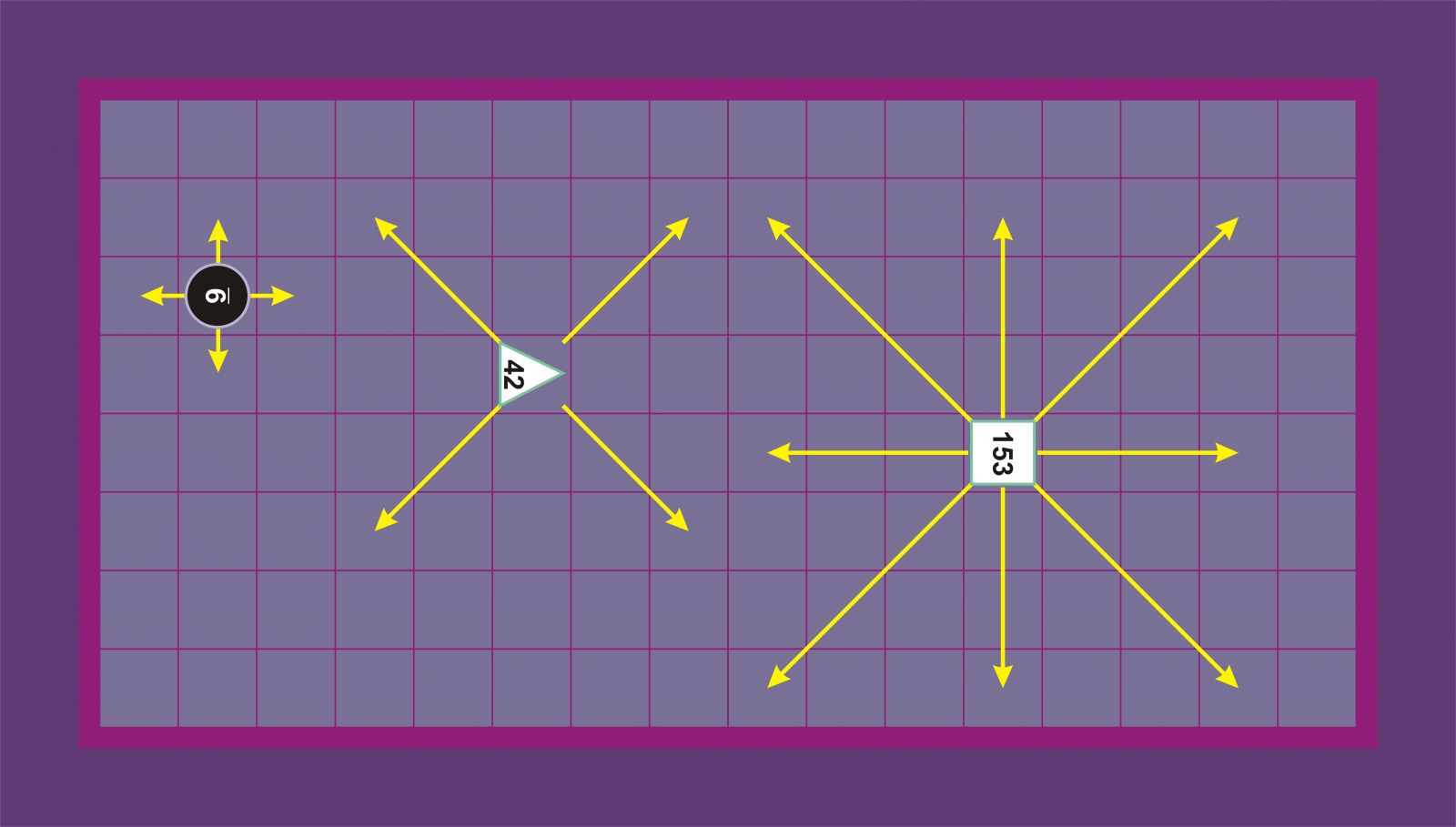
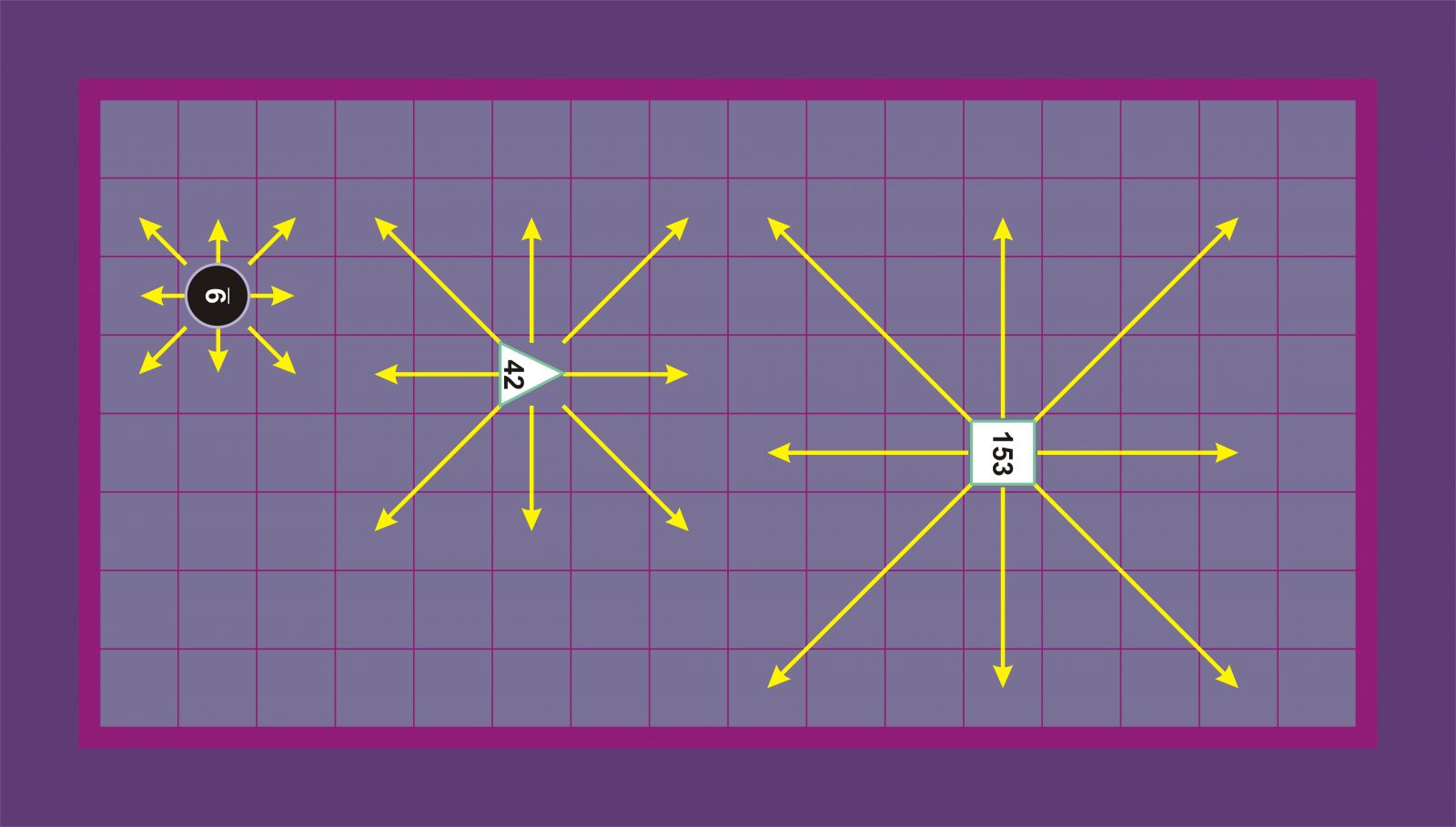
Boissière, Barozzi,Selenus eta katalanezko wikipedia [[1]] Shirwood eta Fulke [[2]]
Shirwoodek eta Fulkek (2. aldaera) honela ematen dute: zirkuluak, triangeluak eta karratuak edozein norabidetan mugitzen dira zehazki lauki bat, bi eta hiru, hurrenez hurren. Fulkek jauziak ere onartzen zituen 2. aldaera horretan [[2]].
Aldaera antzekoa ematen dute Bellek eta Botermansek, baina triangeluak hiru lauki eta karratuak lau lauki mugituz [[3]].
Faberrek eta Fulkek (3. aldaera) honela ematen dute: zirkuluak, triangeluak eta karratuak ortogonalki mugitzen dira zehazki lauki bat, bi eta hiru, hurrenez hurren [[4]].
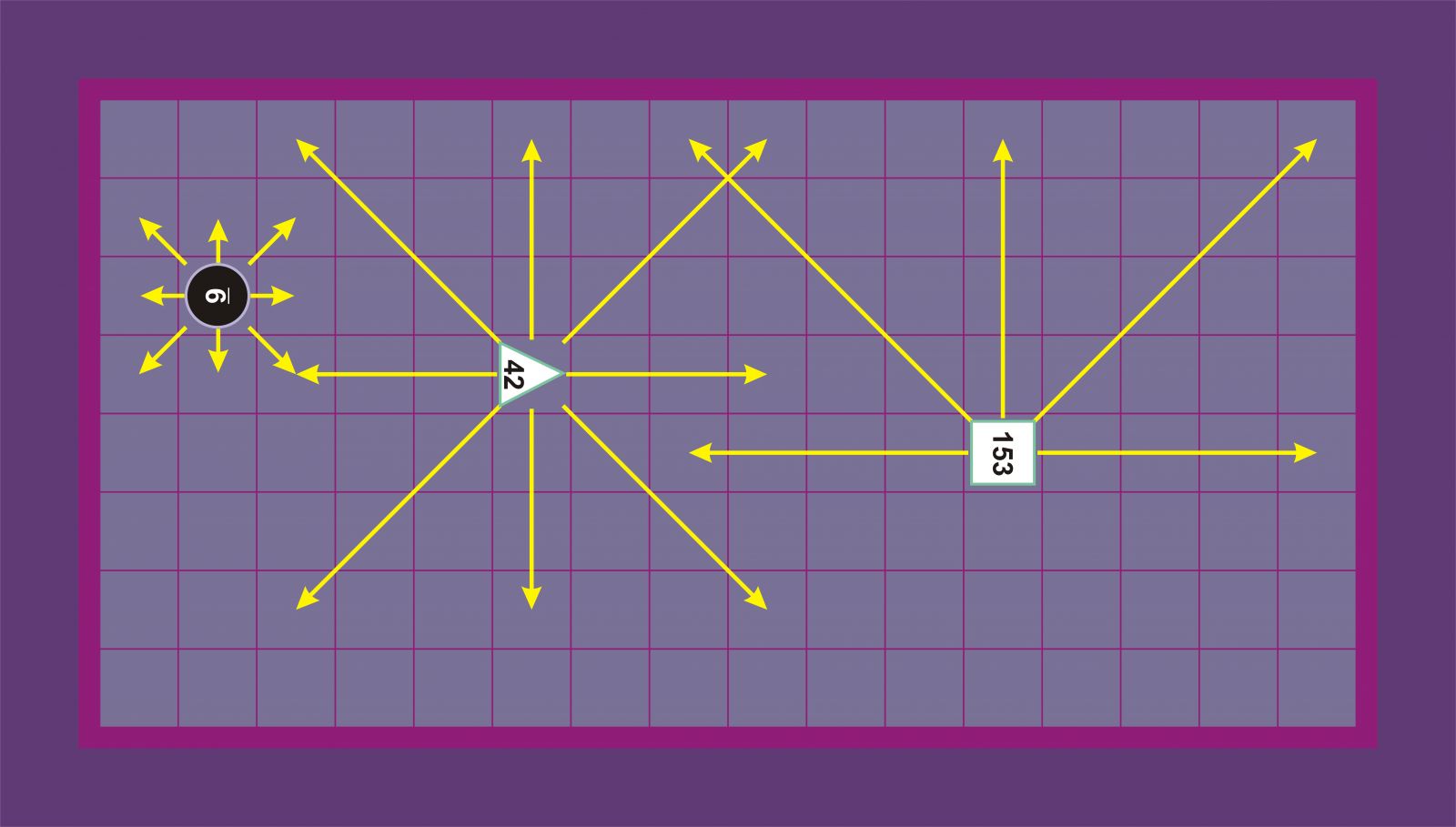
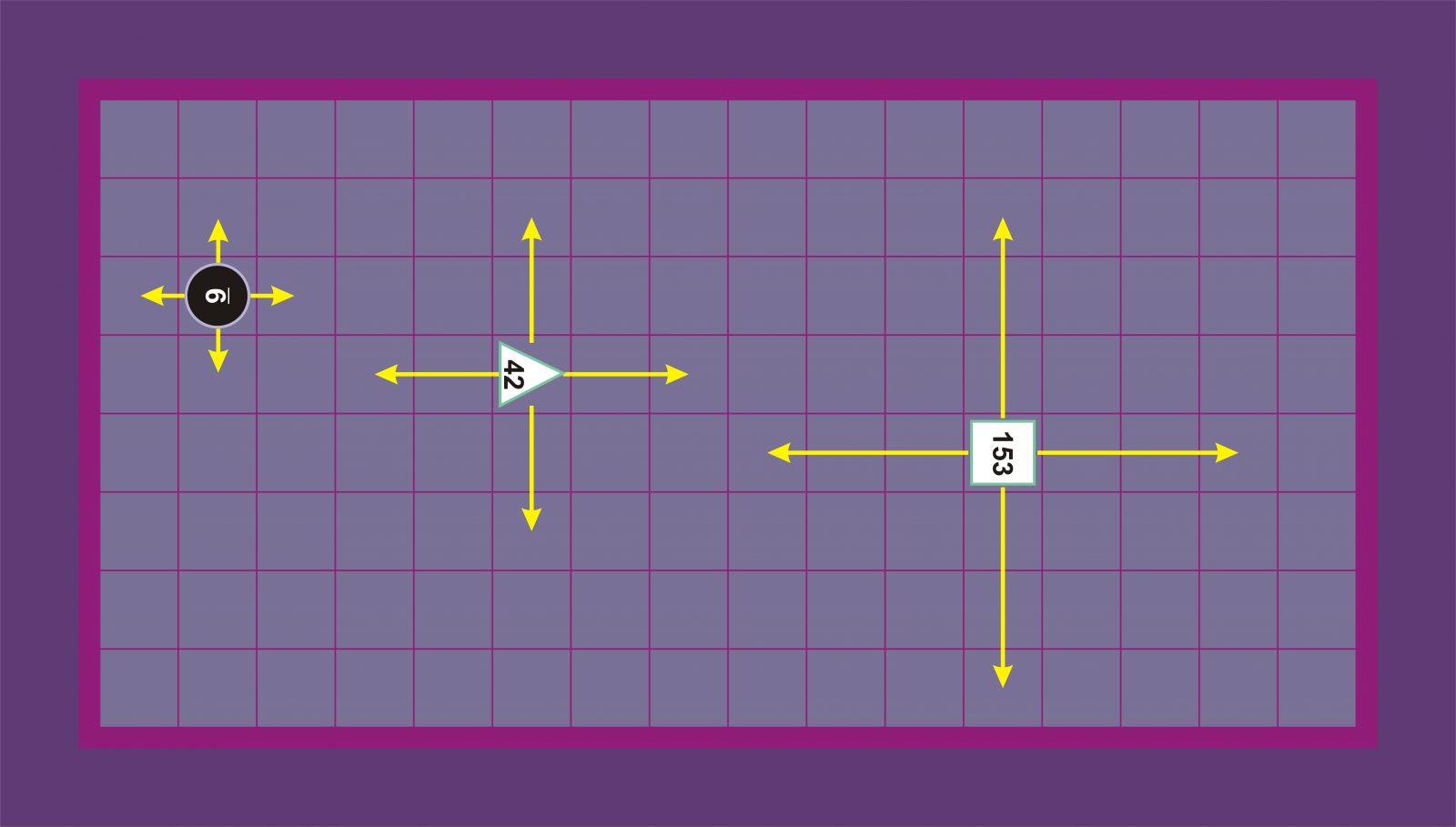
Bell eta Botermans [[3]] Faber eta Fulke [[4]]
Beste aldaera batean, zirkuluak diagonalean lauki huts batera mugitzen dira; triangeluak eta karratuak ortogonalki mugitzen dira zehazki bi eta hiru lauki, hurrenez hurren, bidea beti libre badago. Horrela ematen dute Fulkek, Cazaux-Knowltonek eta gaztelaniazko eta ingelesezko wikipediek. Horrez gain, Fulkek (1. aldaera) triangeluei eta karratuei L moduko mugimendua egiteko aukera ematen die, xakeko zaldiak bezala. Adibidean ez da argi geratzen karratuen kasuan L horrek hiruko edo lauko luzera duen, biak ematen dituelako [[5]].
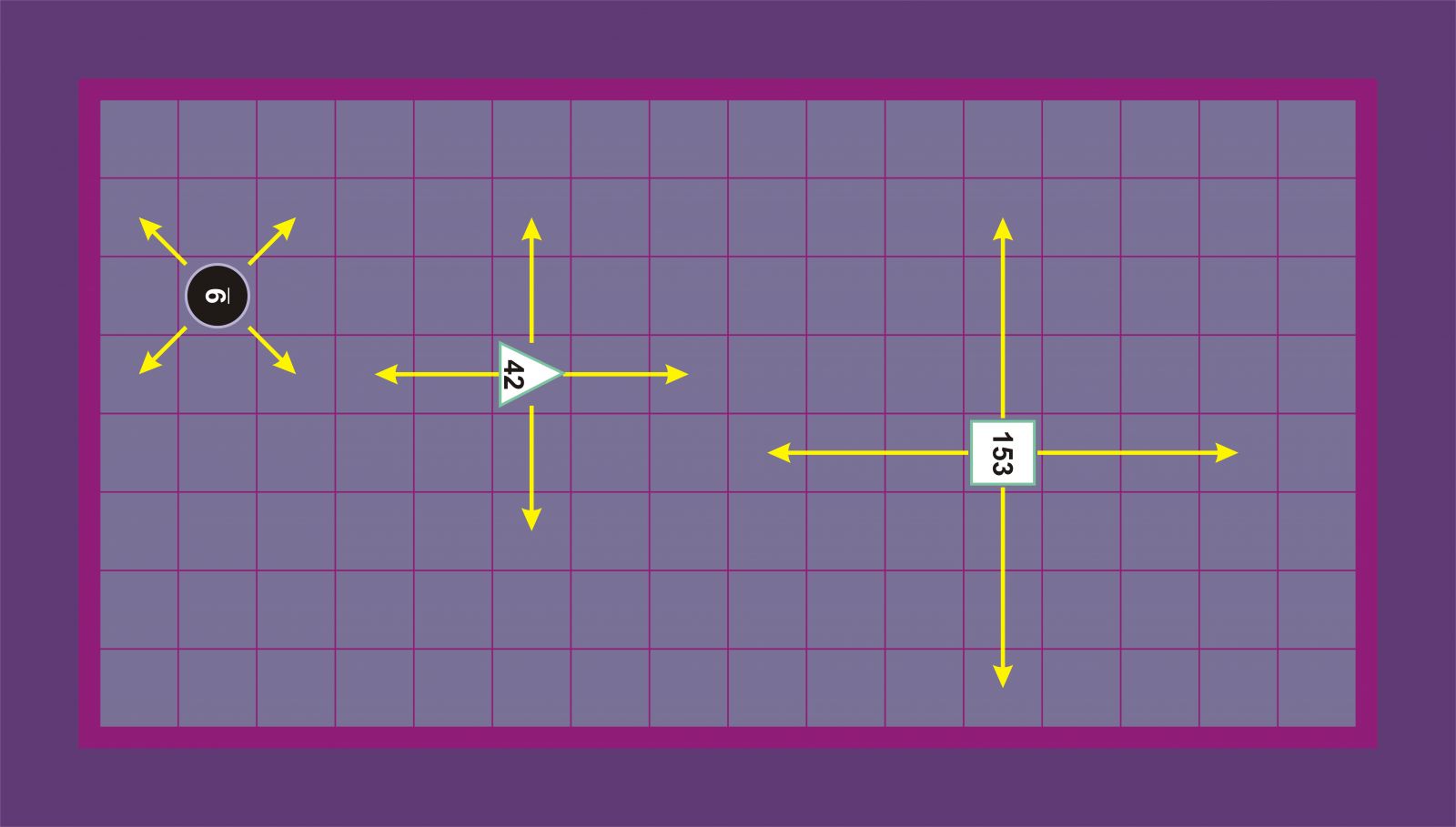
Fulke, Cazaux-Knowlton eta gaztelaniazko eta ingelesezko wikipediak [[5]]
Piramideei dagokienez, testu gehienek onartzen dute piramideek, zirkuluz, triangeluz eta karratuz osaturik daudenez, hiru piezen mugimenduak egin ditzaketela, jokalariaren nahiaren arabera. Piramidea osorik mugitzen da pieza bat balitz bezala. Jakina, piezen mugimenduak egilearen araberakoak direnez, piramidearen mugimenduak ere bai.
Piramideak osorik edo zatika izan daitezke erasoak. Zatikako eraso batean piezaren bat galtzen badute, haien mugitzeko ahalmena ere galtzen dute; baina galera hori ez dago ondo zehaztuta testuetan. Badirudi ideia nagusia dela piramide batek mota bateko piezak galtzen baditu (esaterako, bi karratuak), pieza mota horren mugimendua galtzen duela.
Stigterrek zehazten du piramidea mugitzen dela geratzen zaion pieza baten arabera.
Barozzik piramideei xakeko zaldiaren jauzia egiteko aukera ematen die setiaturik daudenean.
Fulkek piramideei, ohikoaz gain, norabide guztietan ere mugitzeko aukera ematen die, gehienez hiru urrats emanez.
Harrapaketak
Piezak harrapatzea ez da ritmomakia jokoaren helburu nagusia; beraz, piezak harrapatzea ez da derrigorrezkoa.
Núñezek dio harrapaketa guztiak pieza baten mugimendua bukatutakoan gauzatzen direla; mugitu den piezaren eta gainerakoen posizioen arabera, eta ahal bada (piezek lerro zuzenean, ortogonala edo diagonala, egon behar dute, eta bien arteko bidea libre egon), harrapaketa gauzatuko da. Orduan, aurkariaren pieza taulatik aterako da, baina eraso duen pieza bere laukian geratuko da, harrapatutakoaren laukia bete gabe.
Boissierek dio jokalari batek, bere txandan, aurkariaren pieza bat taulatik ateratzea ahazten badu, bere hurrengo txandan, nahi izanez gero, atera dezakeela; baina, orduan pieza aurkariaren laukira mugitu beharko du bere pieza, mugimendu gisa.
Stigterrek zehazten du harrapaketa egiten duen piezak pieza harrapatuaren laukia bete dezakeela. Hori ohiko mugimenduarekin egiten da, setioaren kasuan izan ezik, non mugimendua harrapatutako piezaren mugimendua baita. Urrats hori mugimendu gisa kontatzen da, hau da, hori egiten duen jokalariak ezin du besterik egin.
Cazaux-Knowltonek txanda batean harrapaketa bat baino gehiago egiteko aukera ematen dute: harrapaketa derrigorrezkoa ez bada ere, jokalari bat konturatzen bada aurkariak ez duela harrapaketa bat gauzatu, harrapaketa egin ez duten piezak har ditzake (“haizatuak” esaten dena).
Iturriek piezak harrapatzeko hainbat bide proposatzen dituzte, baina ez dago adostasunik egileen artean. Guk hemen Boissièreri jarraituko diogu, eta horrekin erkatuz beste aldaera batzuk azalduko ditugu.
Pieza aurkari bat topo eginez harrapatuko da balio berdineko pieza batek mugimendu batean pieza horren laukia bete ahal duenean. Boissièrek dio jokalari batek bere txandan aurkariaren pieza bat taulatik ateratzea ahazten badu, hurrengo txandan egin ahal izango duela, nahi izanez gero, baina behartuta egongo dela bere pieza ateratakoaren laukira mugitzera. Bi piezek balio bera badute ere, gerta daiteke batak bestea harrapatzeko aukera izatea, baina besteak bera ez, mugimendu desberdinak dituztelako. Boissièrek eta Barozzik zehazten dute harrapaketa mota hau 9, 16, 25, 36, 49, 64 eta 81 balioetako piezekin baino ezin dela egin, bi jokalariek dituztelako.
Pieza aurkari bat erasoz harrapatuko da pieza baten balioa bera eta pieza aurkari horren artean dauden lauki kopuruaz, mugimenduaren norabidean, biderkatuz edo zatituz pieza aurkariaren balioa berdintzen denean. Ez dago argi lauki kopuru horretan irteerako eta iritsierako laukiak sartzen diren, adibideetan bi aukerak agertzen direlako. Boissièreren eta Barozziren adibideetan ez dira kontuan hartzen piezak dauden laukiak eta kasu posibleen taula ematen dute biek. Fulkek ez du harrapaketa mota hau ematen. Cazaux-Knowltonek tarteko distantzian ez dituzte hartzen piezak dauden laukiak eta ez dute eskatzen bi piezen arteko bidea pieza erasotzailearen mugimenduaren bide bera izatea. Stigterrek, ordea, harrapatzen den piezaren laukia ere kontuan hartzen du. Hala ere, onartzen du batzuetan distantziak harrapatzailearen laukia ere hartzen dela kontuan edo piezek ez dutela zertan lerro zuzenean egon, L moduko bideetan bezala, baina bidea libre egonik.
Pieza aurkari bat segadan harrapatuko da bi edo pieza gehiago hurrengo mugimenduan pieza horren laukia betetzeko posizioan daudenean, eta pieza horien balioen arteko baturak edo kendurak pieza aurkariaren balioa berdintzen dutenean. Boissièrek eta Barozzik bi pieza erasotzaile baino ez dituzte erabiltzen adibideetan. Boissièrek baturaren kasu posibleen taula ematen du, eta Barozzik baturaren eta kenduraren taulak. Cazaux-Knowltonek baturaz eta kenduraz gain, biderkadura eta zatidura ere onartzen dituzte. Stigterrek ere lau eragiketak onartzen ditu, baina araua lau kasutan bereizirik ematen ditu, kenduraren eta zatiduraren kasuetan bi pieza baino ez direla sartzen zehaztuz. Horrez gai, topoz egindako harrapaketa baturaren kasu partikular gisa sartzen du segadan. Botermansek dio pieza bat segadan erortzen dela bi pieza artean harrapatuta geratzen bada, ortogonalean edo diagonalean, eta erabiltzen duen eragiketa bakarra batura da. Berdin esaten du Smith-ek. Ez dute zehazten segada egiten duten bi pieza horiek haien mugimenduekin pieza aurkariaren laukira iristea duten edo ez.
Pieza aurkari bat setioan harrapatuko da piezek pieza hori inguratzen dutenean, mugitzen utzi gabe. Ez dago adostasunik irizpideetan. Boissièrek setioa norabide ortogonaletan egitea proposatzen du; baina orduan, berak onartzen duen bezala, zirkuluei eta piramideei baino ez die eragiten. Barozzik dio pieza aurkaria setioan dagoela ezin bada mugitu berariazko mugimenduetan eta beste pieza lagun batek ezin duenean lagundu setiatzen duten pieza bat harrapatuz. Fulkeren azalpenetan setioa pieza edo piramide setiatuaren mugimendua oztopatzeko laukietan egiten da, eta triangeluen eta karratuen kasuan ez da alboko laukietan zertan izan. Núñezen ustez, logikoa dirudi setiatzeko bete behar diren laukiak pieza aurkariaren motaren araberakoak izatea, mota bakoitzak mugimendu desberdinak dituelako. Botermansek dio setioa lerro ortogonaletan egin behar dela, ez diagonalean. Setioan lagungarriak dira taularen aldeak eta erpinak, bertan pieza gutxiago behar direlako pieza bat setiatzeko. Ez da argi geratzen setiatzen duten piezek pieza setiatuaren ondoz ondoko laukietan egon behar duten.
Cazaux-Knowltonek beste bi bide ematen dituzte piezak harrapatzeko, potentzia eta progresioa. Lehenengoan, pieza harrapatzaileak pieza harrapakinaren laukira iristeko aukera badu, eta pieza harrapatzailearen balioaren potentzia bat edo errodura bat pieza harrapakinaren balioaren berdina bada, harrapatuko du. Bigarrenean, erasotzaileak pieza aurkari baten laukira iristeko bi pieza baditu, eta hiru piezek, harrapatzaileek eta harrapakinak, progresio aritmetiko, geometriko edo harmoniko bat osatzen badute, pieza aurkaria harrapa dezake.
Piramideen aurkako erasoa berezia da haien osaketagatik. Hemen ere desadostasunak daude egileen artean. Gehienek diote piramide osoa setioaren bidez harrapa daitekeela. Botermansek dio ezta horrela ere ezin dela harrapatu. Eta Stigterrek eransten du osorik harrapa daitekeela batura osoa edo piramidearen beheko karratua, 64 argia eta 36 iluna, harrapa daitezkeenean gainerako harrapaketa motekin.
Botermansek dio piramide osoa harrapatzeko, lehenago beheko karratua harrapatu behar da. Ondoren, (geratzen den) piramide osoa harrapa daiteke, gainerako pieza bat nahi den eran harrapatuz. Baina, piramidearen bigarren pieza hori arriskuan dagoenean, piramidearen jabeak erasotzaileari arriskuan dagoen piezaren balioa bera duen beste pieza bat edo, holakorik ez badu, edozein pieza eskain diezaioke trukean. Erasotzaileak aukera du eskaintza onartzeko, eta eskainitako pieza harrapatuko du, edo errefusatzeko, eta piramidea harrapatuko du.
Denek onartzen dute piramidearen piezak banaka harrapa daitezkeela, baina aldeak daude batetik bestera. Stigterrek dio piramidea zatika harrapa daitekeela pieza bat harrapatzeko erabiltzen diren setioa izan ezik gainerako bideen bidez; kasu horretan harrapatzaileari eskain dakioke pieza harrapatuaren balio bera duen beste pieza bat, taulan egonez gero. Baina, zer esan nahi du? Piramide osoa harrapatzen dela edo piramidea deseraikitzen dela. Setioz gain, Cazaux-Knowltonen arabera, piramidea zatika ere harrapa daiteke, aldi bakoitzean piramidearen pieza bat harrapatuz. Ez dago argi piezak behetik gora edo beste edozein ordenatan harrapatu behar diren eta uler daiteke piramidearen pieza guztiak banan-banan harrapa daitezkeela piramidea bukatu arte.
Piramideen erasotzeko ahalmena geratzen zaizkion piezen araberakoa izango da, oro har. Ez da zehazten balio osoa geratzen zaizkion piezen batura den edo hasierako balioa, 91* eta 190*. Núñezen arabera, piramideak galtzen duen osagai bakoitzeko bere erasotzeko ahalmena ere txikiagotzen da, eta ezin du bere balio osoarekin (91* edo 190*) eraso, geratzen zaion pieza baten balioarekin baizik. Cazaux-Knowltonen arabera, piramideak mugitzeko bezala jokatuko du erasotzeko, bere balio osoa edo pieza baten balioa soilik hartuz. Stigterrek dio piramideak pieza bat harrapa dezakeela bi eratan: lehena, bera osatzen duen pieza batek bezala, setioan izan ezik, piramidearen mugimendua pieza horrena izanik eta zehazten du ezin dela pieza bat baino gehiago erabili harrapaketarako. Eta bigarrena, piramideak bere uneko osagaien batura erabil dezakeela harrapaketa mota guztiekin, aurreko aukera erabili gabe txanda horretan. Eta bi kasuetan eransten du mugimendua hautatutako piezatik independentea dela. Mebbenen arabera, piramideen banakako osagaiek harrapa dezakete eta harrapatuak izan daitezke. Osagairen bat falta bazaio, piramideak harrapatuak izan daitezke batura osoagatik, baina, kasu horretan, haiek ezin dute piezarik harrapatu haien batura osoarekin. Batura partzialak onartezinak dira.
Harrapatutako piezak
Ez dago adostasunik harrapatutako piezen inguruan. Jokalari batek pieza bat harrapatzen zuenean, pieza harrapatuaren jabeak berak aurretik harrapatutako pieza batez ordezka zezakeen. Adibideetan ez da argi ikusten ordezkapena zenbakizko balio bereko pieza batez edo forma bereko pieza batez egin behar zen. Ez dago argi ordezkapen hori piramide bat osatzen duten piezak erasotzean bakarrik edo gainerako piezak erasotzean ere egin zitekeen. Jacques Lefèvre d’Étaples-ek ordezkapena onartzen zuen aurretik harrapatutakoen artean balio bereko pieza bat zegoenean.
Barozzik bere bosgarren arauan dio harrapatutako pieza guztiak eta piramideen osagai guztiak taulatik kanpo harrapatzailearen aldean geratu behar direla ahoz behera, horren piezen koloreko bihurtzeko eta horrek nahi duen unean eta lekuan erabil ditzan, batzuk edo guztiak taulara nahierara sartzeko.
Fulkek dio harrapatutako edozein pieza harrapatzailearen kolorearekin gora jarri behar dela, eta haren eremuko azkeneko laukian jarri, eta handik aurkari berrien kontra jo eta jabe berria lagundu irabazten.
Cazaux-Knowltonek diote, ordea, erasotako pieza taulan gera daitekeela, baina leialtasuna aldatzen du. Kasu horretan, bere lekuan irauli besterik ez da egiten, zenbaki eta forma bera erakutsiz, baina kolorez aldatuz. Aldeak aldatu dituen pieza bat ezin da mugitu edo bigarren aldiz harrapatu. Bere laukian jarraitzen du, mugiezina eta geldiezina, baina zenbakizko konbinazioetan parte har dezake jabe berriaren mesedetan.
Núñezek, koherentziaz, iradokitzen du errepikatzen diren balioak dituzten piezak baino ezin direla ordezkatu, hau da, zenbaki karratuak; gainera, batzuk piramideen osagaiak dira.
Garaipenak
Bide batzuk daude ritmomakian garaipena lortzeko, denak loriatsuak ez izan arren. Bi kategoriatan sailkatu ohi dira: garaipen arruntak eta berariazko garaipenak.
Garaipen arruntak hasiberriak entrenatzeko garaipenak izango ziren. Boissièrek bost garaipen arrunt eman zituen:
Gorputzaren garaipenak harrapatutako pieza kopurua baino ez du kontuan hartzen. Jokalariek partida hasieran adostuko dute kopuru hori, eta lortzen duen lehena izango da irabazlea.
Ondasunen garaipenak harrapatutako pieza guztien balioa baino ez du kontuan hartzen. Aurrekoan bezala, jokalariek balio hori adostuko dute partida hasieran.
Prozesu-garaipenak harrapatutako piezetan dagoen zifra kopurua hartzen du kontuan, ez balioa. Adibidez, batak 16, 20, 25 piezak (hiru pieza eta 61 puntu) harrapatu baditu eta besteak 5, 7, 9, 49 piezak (lau pieza eta 70 puntu), lehenak irabazi du sei zifra lortu dituelako, eta bigarrenak bost zifra. Aurrekoetan bezala, jokalarien adostasuna behar da zifra kopuru hori erabakitzeko. Fulkek, Botermansek eta Cazaux-Knowltonek zifra kopuruarekin batera piezen zenbakien batura ere eskatzen dute. Horrela, jokalariek batura bat zenbat zifrarekin lortuko (edo gaindituko) duten adostu behar dute.
Ohorezko garaipenak harrapatutako piezen kopurua eta balioa hartzen ditu kontuan. Hau da, irabazleak adostutako pieza kopuru zehatza eta piezen balioa lortu edo gainditu behar ditu.
Ohorezko eta prozesuko garaipenak hiru irizpideak hartzen ditu kontuan, pieza kopurua, piezen balioa eta piezen zifra kopurua. Jokalariek kopuruak adostu behar dituzte partida hasieran. Hau da, irabazleak adostutako batura lortu edo gainditu behar du pieza kopuru zehatzean eta piezen zifra kopuru zehatzean.
Berariazko garaipenak jokoaren funtsa dira; ez dute kontuan hartzen aurkariaren piezen harrapaketa, baizik eta norberaren piezen posizioa, aurkariaren eremuan, egitura erregular batean, halako moduan non piezen balioek harmonia bat erakusten duten.
Fulkek aurkariaren eremua ezartzen du haren lehen piezen lerrotik, hasierako posizioan, eta taularen bukaeraraino, 40 lauki hartuz, edo batzuek nahi bezala 48. Fulkeren hasierako posizioa kontuan hartuz, 48 lauki izango lirateke, 6×8. Stigterrek dio aurkariaren eremua haren aldeko taula erdia dela.
Boissièrek berariazko hiru garaipen eman zituen:
Hala moduzko garaipena lortzen du jokalariak aurkariaren eremuan hiru pieza sartzen dituenean harmonia hauetako bat osatuz: progresio aritmetikoa, progresio geometrikoa edo progresio musikala (harmonikoa) [2]. Adibideak: aritmetikoa, 3, 5, 7 pieza ilunak; geometrikoa, 9, 12, 16 pieza ilunak; harmonikoa, 9, 16, 72 pieza argiak.
Garaipen handia lortzen du jokalariak aurkariaren eremuan lau pieza sartzen dituenean zenbait harmonia osatuz; esaterako, aritmetikoa eta geometrikoa, edo aritmetikoa eta harmonikoa, edo geometrikoa eta harmonikoa.
Garaipen bikaina lortzen du jokalariak aurkariaren eremuan hiru harmoniak dituzten lau pieza sartzen dituenean.
Hiru garaipenetan adostasuna dago, baina ez harmonia hori erakusten duten piezen posizioan. Boissièrek ez zituen posizio horiek eman, aurkariaren eremuan izan behar zela baino ez zuen esan. Cazaux-Knowltonek diote, hala moduzko garaipenean, piezek lerro ortogonal edo diagonal batean egon behar dutela, eta distantzia berdinera eta ordena gordez; eta eransten dute egile batzuek angelu zuzen bat osatzea ere onartzen dutela. Garaipen handian, ordea, ez dute eskatzen piezek distantzia berdina gordetzeko. Mebbenek dio piezak goranzko lerro batean, angelu zuzenean edo, lau izanik, karratu baten erpinetan kokatu behar direla, eta elkarrengandik distantzia berdinera. Piezen posizioz gain, piezen ordena ere kontuan hartu behar da. Baina horretaz ere ez dago argibiderik. Fulkeren adibidean ikusten da ez duela ordena gorakorra edo beherakorra eskatzen: 5, 1, 3. Piezak ordenan, gorakorrean edo beherakorrean, jartzeko eskatzen bada, helburua zaildu egingo da. Stigterrek dio piezak zenbakien arabera ordenatu behar direla eta distantzia berdinera jarri behar direla, lerro ortogonal edo diagonal batean, eta piezarik gabe tartean. Dio ere maiz angelu zuzenean jartzea ere onartzen dela.
Badago beste kontu bat garaipenen inguruan eta hierarkiak osatzerakoan harrapatutako piezak erabiltzeko aukera da. Testu klasikoek aukera hori ikusten dute, baina ez dute baldintzarik ematen. Ez dakigu zenbat pieza eta zeintzuk erabil daitezkeen. Eta egungo adituek ere ez dute ezer argitu. Mebbenek, ordea, dio harrapatutako piezak erabiltzeak harmoniak osatzea errazten duela, baina ez dela komeni harmonia osatzen duen azken pieza izatea.
[2] Har ditzagun a, b, c zenbakiak. Progresio aritmetikoan daude c – b = b – a betetzen bada. Progresio geometrikoan daude c / b = b / a betetzen bada. Progresio harmonikoan daude c / a = ( c – b ) / ( b – a ) betetzen bada.
Arauak
Ritmomakia berreskuratu nahiko bagenu, arauak bateratu beharko genituzke. Arau batzuk eman aurretik, beraz, hausnarketa bat. Ritmomakiari buruz idazten den artikulu bakoitzean egileak bere arauak ematen baditu, aurrekoak kontuan hartuz edo hartu gabe, arrisku handia dago arau-sorta berri bat emateko.
Hasierako posizioa
Jokalariak taularen alde luzeetan jarriko dira aurrez aurre eta piezak beraien ezkerretik eskuinera eramango dituzte.
Bi jokalarien piezak honela kokatuko dira taulan. Pieza argiekin jokatzen duen pertsona beheko aldean jarriko da, eta pieza ilunekin jokatzen duena goiko aldean.
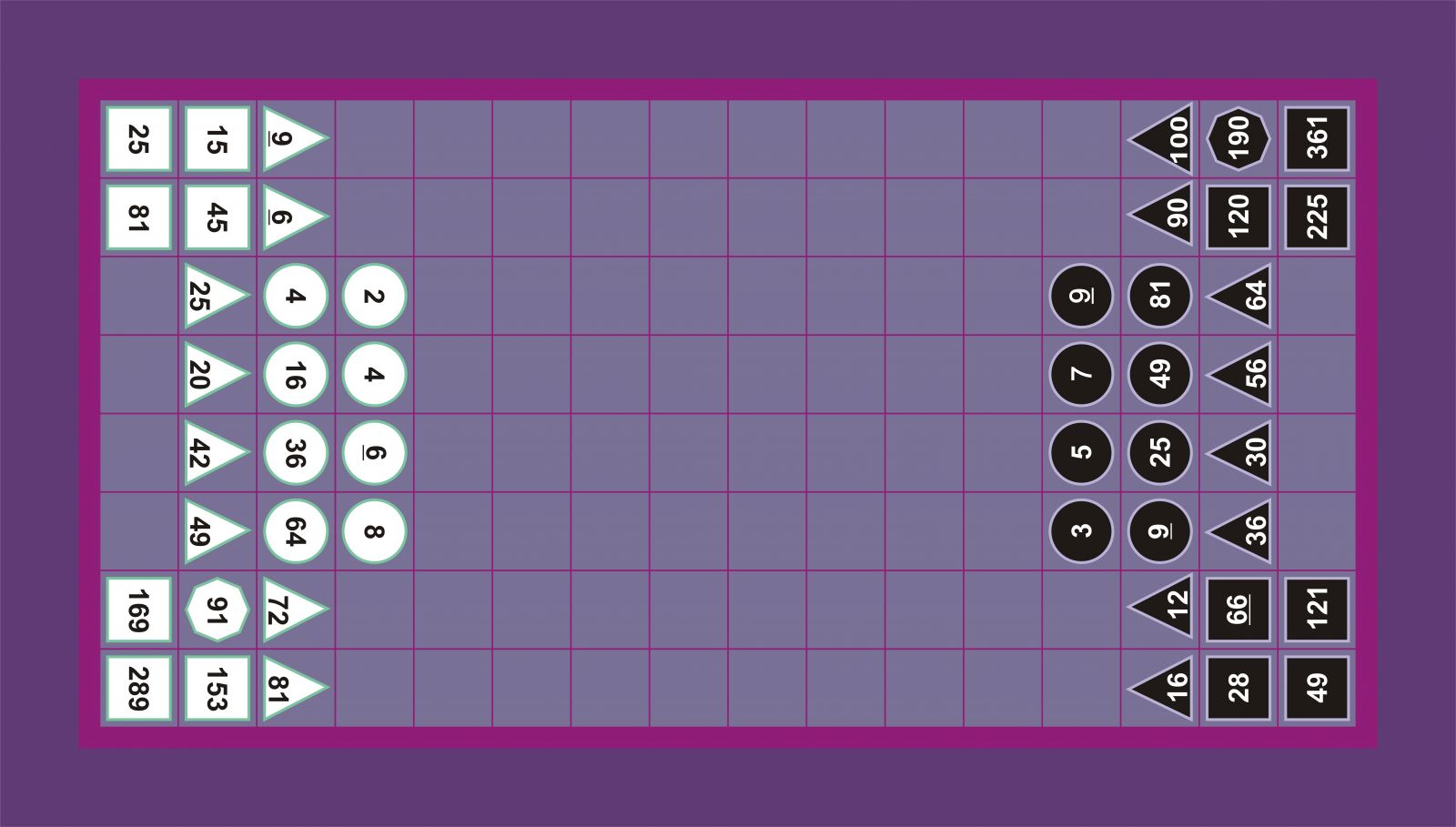
Helburua
Partida hasieran, jokalariek adostu behar dute irabazteko helburua, edo garaipen arruntak edo berariazko garaipenak; lehenengoen kasuan, bost garaipenetatik bat adostu behar dute.
Garaipen arruntak
1. Gorputzaren garaipena: jokalariek adostuko dute aurkariaren zenbat pieza harrapatu behar diren, partida irabazteko.
2. Ondasunen garaipena: jokalariek adostuko dute zenbat izan behar duen harrapatutako piezen balioen baturak, gutxienez, partida irabazteko.
3. Prozesu-garaipena: jokalariek adostuko dituzte zenbat izan behar duen gutxienez harrapatutako piezen balioen baturak eta zenbat zifra izan behar duten zehazki harrapatutako piezek, partida irabazteko. Adibidean, 200 puntu eta zortzi zifra:

4. Ohorezko garaipena: jokalariek adostuko dituzte aurkariaren zenbat pieza harrapatu behar diren zehazki eta pieza horien balioen baturak zein izan behar duen, gutxienez, partida irabazteko. Adibidean, 200 puntu eta bost pieza:

5. Ohorezko eta prozesuko garaipena: jokalariek adostuko dituzte aurkariaren zenbat pieza harrapatu behar diren zehazki, pieza horiek zenbat zifra izan behar duten zehazki eta pieza horien balioen baturak zein izan behar duen, gutxienez, partida irabazteko. Adibidean, 200 puntu, bost pieza eta zortzi zifra:

Berariazko garaipenak
Hala moduzko garaipena: jokalari batek partida bat irabaziko du, aurkariaren eremuan, hiru piezarekin progresio aritmetikoa, progresio geometrikoa edo progresio harmonikoa osatzen badu.
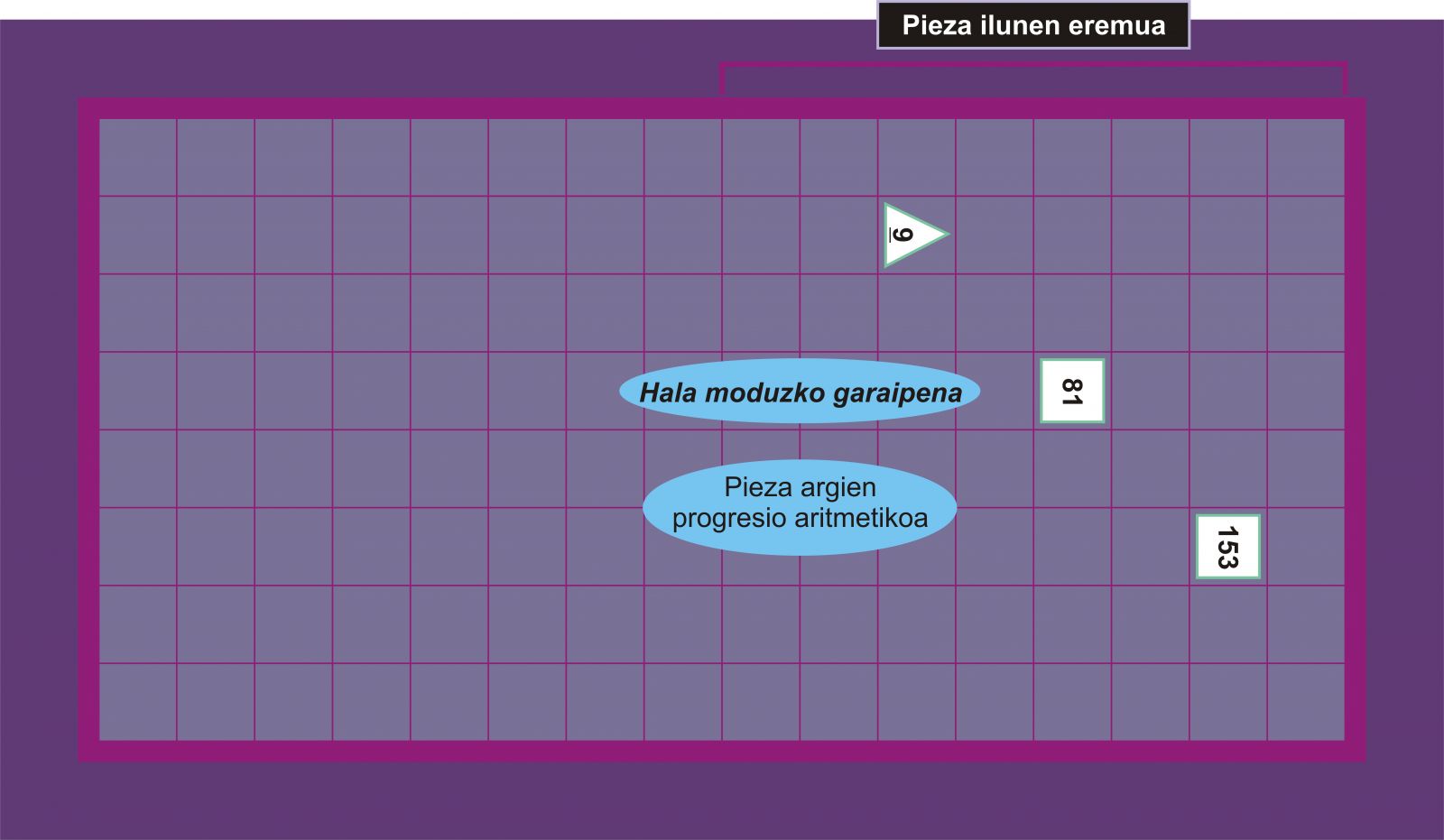
Garaipen handia: jokalari batek partida bat irabaziko du, aurkariaren eremuan, lau piezarekin progresio aritmetikoa eta progresio geometrikoa, edo progresio aritmetikoa eta progresio harmonikoa, edo progresio geometrikoa eta progresio harmonikoa osatzen baditu. Hau da, lau piezarekin bi progresio osatu behar dira.
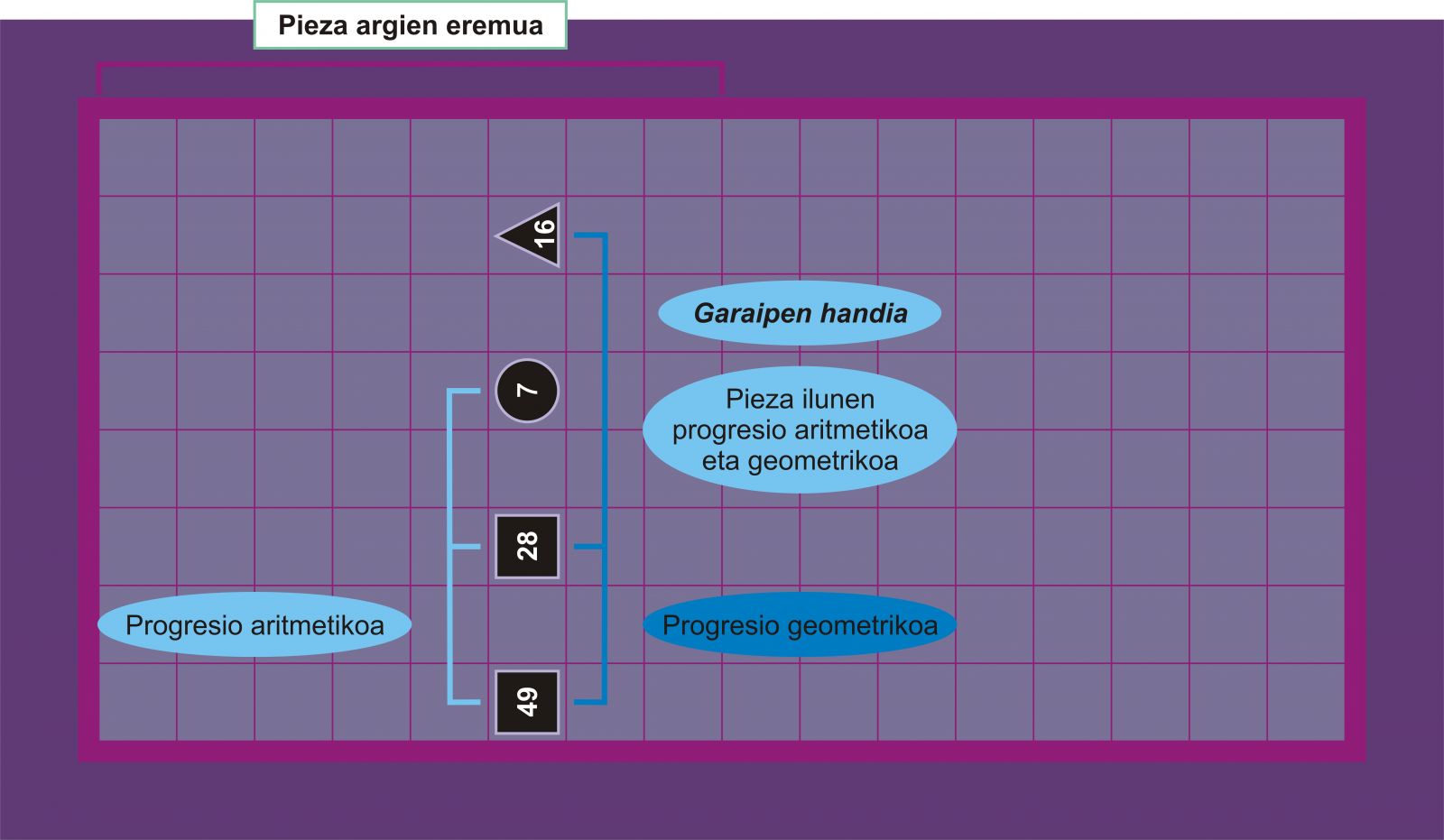
Garaipen bikaina: jokalari batek partida bat irabaziko du, aurkariaren eremuan, lau piezarekin progresio aritmetikoa, progresio geometrikoa eta progresio harmonikoa osatzen baditu. Hau da, lau piezarekin hiru progresioak osatu behar dira.
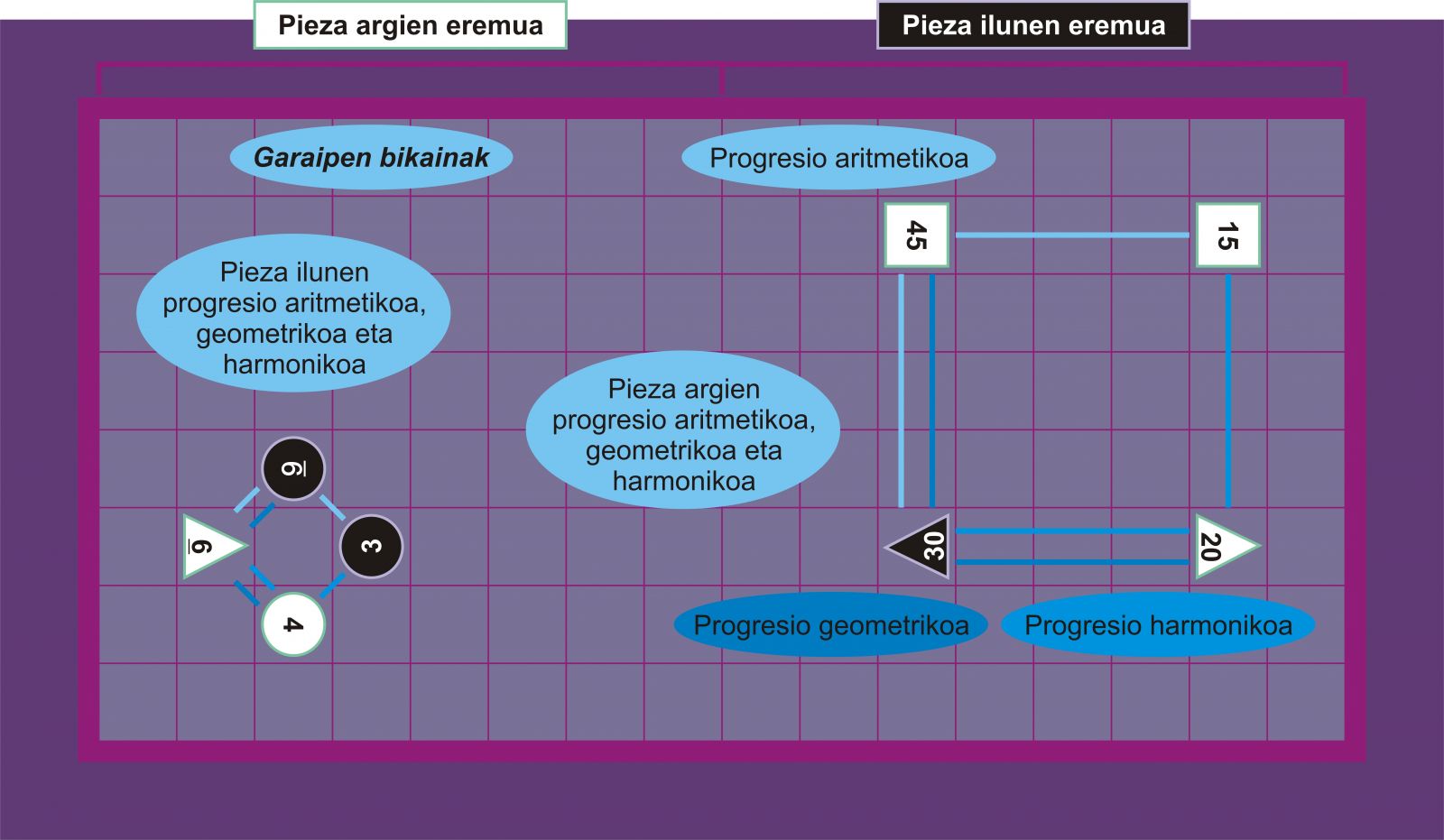
Progresioak osatzen dituzten piezak lerro zuzen batean, horizontal, bertikal edo diagonalean, ondoz ondoko piezen arteko distantziak berdinak izanik, edo karratu baten erpinetan jarri behar dira. Progresioak bi jokalarien piezekin osa daitezke. Piezen balioek ez dute zertan ordena gorakorrean egon.
Mugimenduak
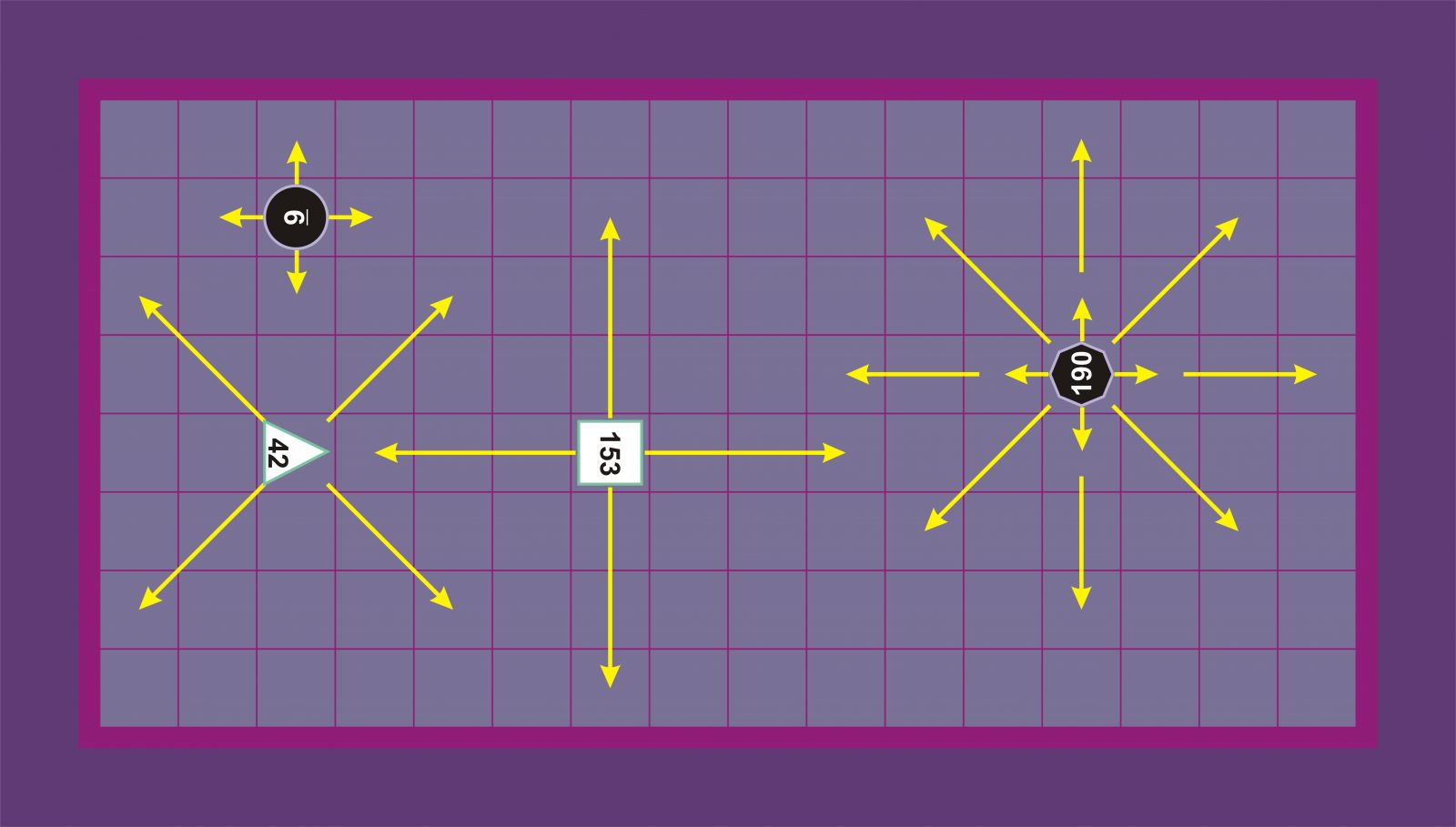
Zirkuluak aldameneko lauki huts batera mugituko dira ortogonalki, hots, aurrera-atzera edo esker-eskuin.
Triangeluak zehazki bigarren laukira mugituko dira diagonalean, laukia eta bidea libre badaude.
Karratuak zehazki hirugarren laukira mugituko dira ortogonalki, laukia eta bidea libre badaude.
Piramideak osatzen dituzten piezen mugimenduen arabera mugituko dira une oro, jokalariaren nahierara. Piramideak osorik mugitzen dira pieza bakarra balira bezala. Piramideak mota bateko piezak galtzen dituenean, pieza mota horren mugimendua galduko du.
Harrapaketak
Lau dira aurkariaren piezak harrapatzeko bideak.
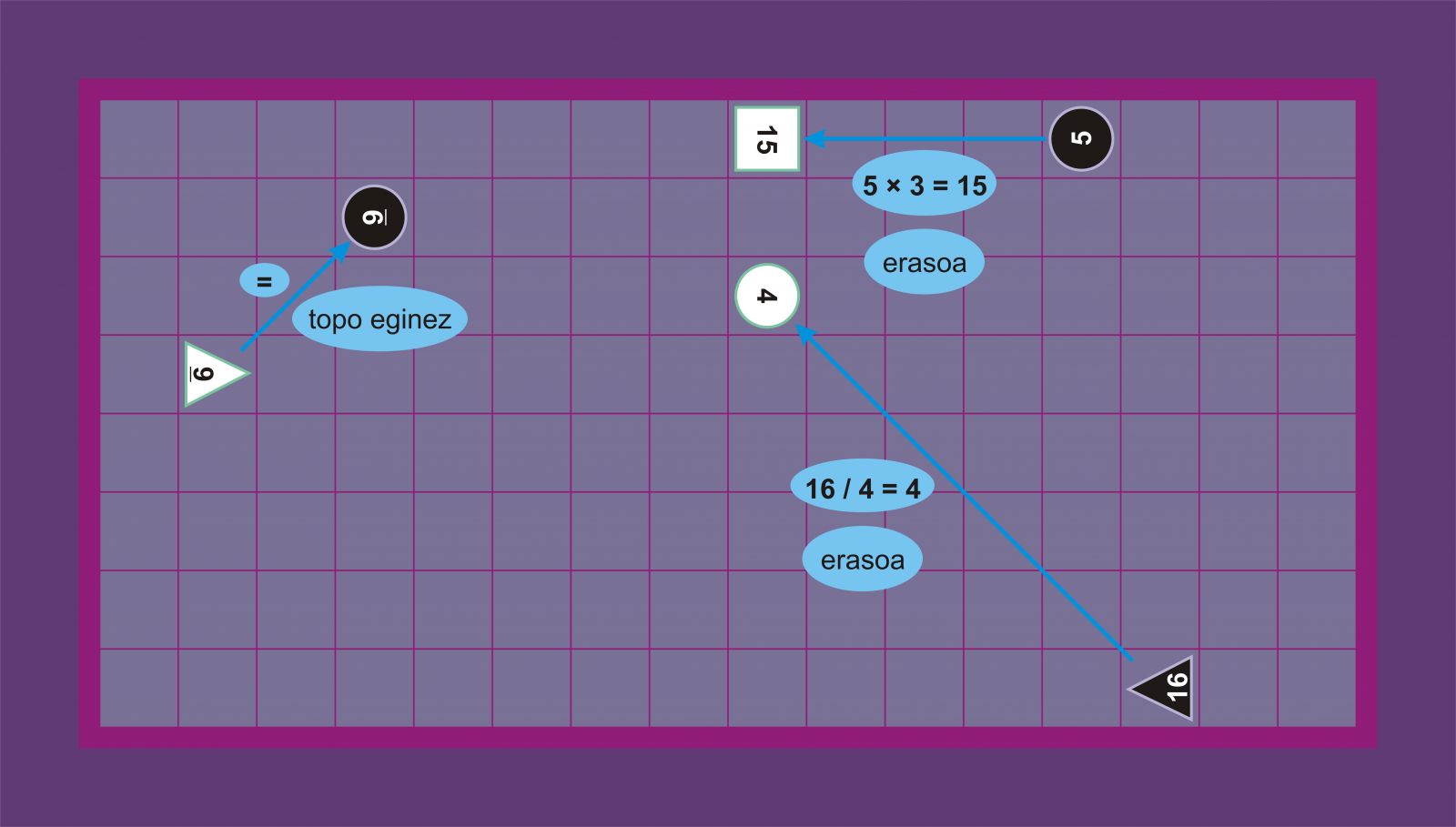
Jokalari batek topo eginez harrapatuko du aurkariaren pieza bat aurkariaren piezaren balio bera duen bere pieza batek mugimendu batean pieza horren laukia bete ahal duenean. Orduan, aurkariaren pieza taulatik aterako du, baina pieza erasotzaileak ez du haren lekua beteko, dagoen lekuan geratuko da.
Jokalari batek erasoz harrapatuko du aurkariaren pieza bat, bere pieza baten balioa bi piezen artean dauden lauki hutsen kopuruaz biderkatuz edo zatituz aurkariaren piezaren balioa berdintzen duenean; bi piezen artean dauden lauki hutsak pieza erasotzailearen mugimenduaren arabera zenbatuko dira. Aurkariaren pieza taulatik aterako du, baina pieza erasotzailea ez da bere lekutik mugituko.
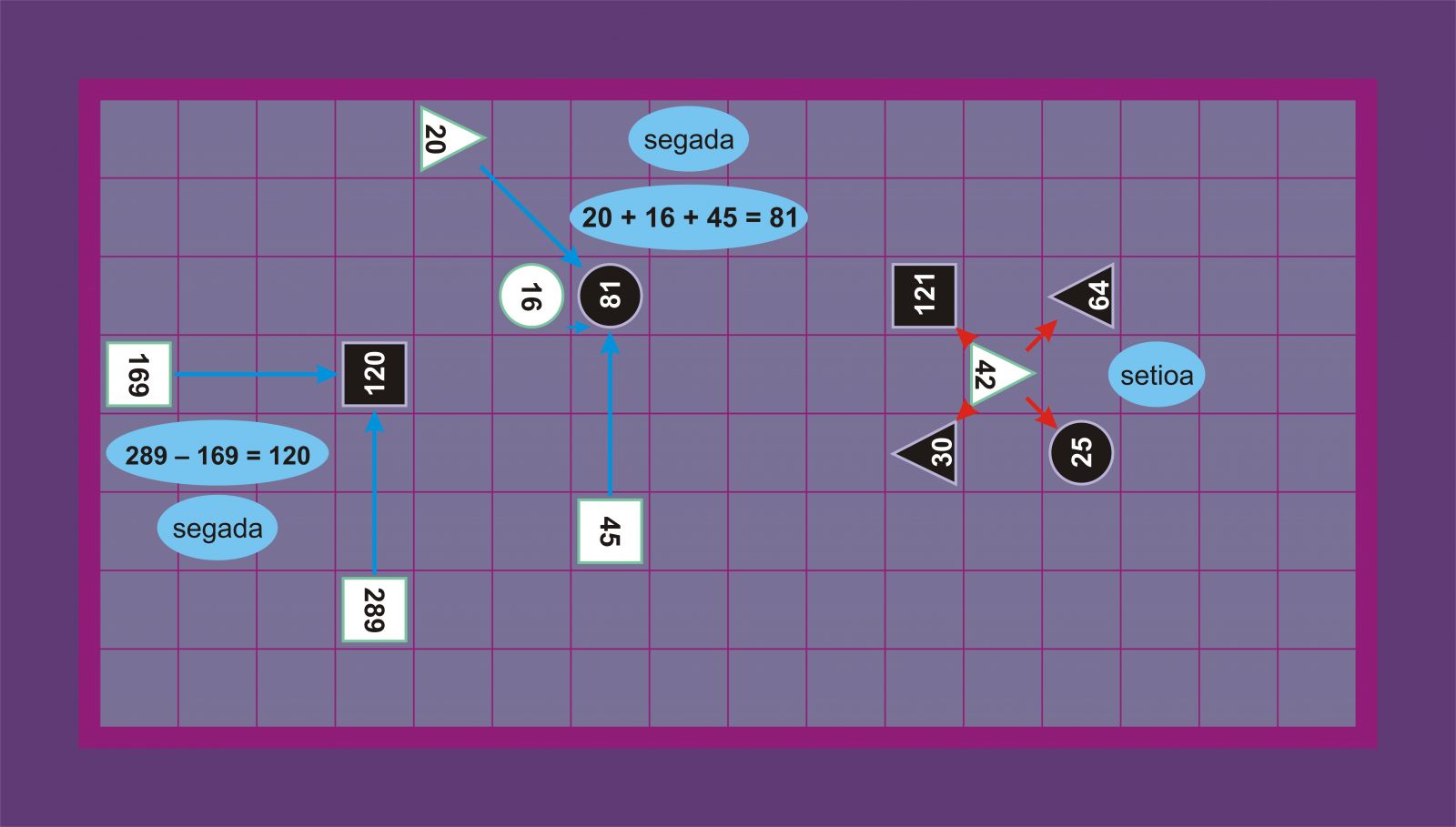
Jokalari batek segadan harrapatuko du aurkariaren pieza bat, bere bi pieza hurrengo mugimenduan pieza horren laukia betetzeko posizioan daudenean, eta pieza horien balioen arteko baturak edo kendurak pieza aurkariaren balioa berdintzen dutenean. Kasu horretan, aurkariaren pieza taulatik aterako du, baina pieza erasotzaileak dauden lekuan geratuko dira.
Jokalari batek setioan harrapatuko du aurkariaren pieza bat, bere piezekin pieza aurkaria inguratzen duenean mugitzen utzi gabe, hau da, pieza aurkariaren mugimendua oztopatzen dutenean. Pieza setiatzaileek pieza setiatuaren ondoko laukietan egon behar dute. Kasu horretan, aurkariaren pieza taulatik aterako du, baina pieza erasotzaileak dauden lekuan geratuko dira. Inguratutako pieza aurkariak inguratzen duen piezaren bat harrapatzerik baldin badu, ez dago harrapaturik. Harrapaketa mota honetan piezen balioa ez da erabiltzen. Setioan lagungarriak dira taularen aldeak eta erpinak, bertan pieza gutxiago behar direlako pieza bat setiatzeko.
Piramideak osorik harrapa daitezke aurreko metodoen bidez, unean duen balioarekin. Kontuan hartu behar da, hasieran, piramide oso bat setiatzeko zortzi pieza behar direla.
Horrez gain, piramideak deseraiki daitezke haien piezak banaka harrapatuz aurreko metodoen bidez, piramidea desagertu arte.
Piramide osoak erabil daitezke harrapaketetarako, unean uneko balioarekin. Piramideen piezak banaka erabil daitezke harrapaketak egiteko; orduan, piramidearen ahalmena pieza erasotzaile horrena da eta harrapaketa pieza horrek egingo balu bezala egin behar da.
Pieza bat harrapatzen denean, pieza taulatik ateratzen da, bere laukia hutsik utziz. Pieza harrapatzaileak ez du haren lekua beteko txanda horretan. Hurrengo txandan bete nahi badu, hori izango da bere mugimendua.
Ritmomakiako piezen matematika
Jokoaren piezak hiru formatakoak dira: karratuak, triangeluak eta zirkuluak. Pieza bakoitzak zenbakizko balio bat dauka. Jokalari bakoitzak 24 piezak ditu, zazpi karratu, zortzi triangelu eta zirkulu eta piramide bat.
Pieza argiek zenbakizko balio hauek dituzte: zirkuluetan, 2, 4, 4, 6, 8, 16, 36, 64; triangeluetan, 6, 9, 20, 25, 42, 49, 72, 81; karratuetan, 15, 25, 45, 81, 153, 169, 289; eta piramidean, 91*.
Pieza ilunek zenbakizko balio hauek dituzte: zirkuluetan, 3, 5, 7, 9, 9, 25, 49, 81; triangeluetan, 12, 16, 30, 36, 56, 64, 90, 100; karratuetan, 28, 49, 66, 120, 121, 225, 361; eta piramidean, 190*.
Horrela ikusita zenbaki horiek ez dute iradokitzen inolako egitura matematikorik. Baina beste era batean antolatuta egitura matematiko hori ikusiko dugu. Lehendabizi, Boezioren ikuspuntu zaharra erabiliko dugu. Boeziok zenbaki handiagoak bost mailatan sailkatzen zituen; lehenengo hirurak baino ez dira agertzen ritmomakiaren piezetan: multiploak (multiplex), beste zenbakia hainbat aldiz hartzen zuen osorik, 9ak hiru aldiz hartzen du 3a; superpartikularrak (superparticularis) beste zenbakia behin osorik eta haren zati bat hartzen zituen, 6ak 4a behin eta 4aren erdia hartzen ditu, 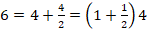 ; superpartienteak (superpartiens) beste zenbakia behin eta haren zenbait zati hartzen zituen, 15ak 9a behin eta 9aren bi heren hartzen ditu,
; superpartienteak (superpartiens) beste zenbakia behin eta haren zenbait zati hartzen zituen, 15ak 9a behin eta 9aren bi heren hartzen ditu, 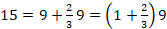 ; multiplo superpartikularrak (multiplex superparticularis) eta multiplo superpartienteak (multiplex superpartiens). Horren arabera, honela eman ditzakegu ritmomakiaren piezen banaketa:
; multiplo superpartikularrak (multiplex superparticularis) eta multiplo superpartienteak (multiplex superpartiens). Horren arabera, honela eman ditzakegu ritmomakiaren piezen banaketa:
| Argiak | Ilunak | |||||||
|
2 |
4 |
6 |
8 |
Zirkuluak multiploak |
3 |
5 |
7 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Triangeluak superpartikularrak |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Karratuak superpartienteak |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gaur egun, aljebraren idazkera erabiliz, honela emango genuke ritmomakiaren piezen banaketa:
| Argiak | Ilunak | ||||||||
| zirkuluak |
2 |
4 |
6 |
8 |
|
3 |
5 |
7 |
9 |
|
4 |
16 |
36 |
64 |
|
9 |
25 |
49 |
81 |
|
| triangeluak |
6 |
20 |
42 |
72 |
|
12 |
30 |
56 |
90 |
|
9 |
25 |
49 |
81 |
|
16 |
36 |
64 |
100 |
|
| karratuak |
15 |
45 |
91* |
153 |
|
28 |
66 |
120 |
190* |
|
25 |
81 |
169 |
289 |
|
49 |
121 |
225 |
361 |
|
Izartxoa daramaten karratuak, 91* argietan eta 190* ilunetan, piramideak dira eta honela osatzen dira:
Piramide argia: 36ko karratua, 25eko karratua, 16ko triangelua, 9ko triangelua, 4ko zirkulua eta 1eko zirkulua, guztira 91*.
Piramide iluna: 64ko karratua, 49ko karratua, 36ko triangelua, 25eko triangelua eta 16ko zirkulua, guztira 190*.
Bi zenbaki horiek zenbaki poliedrikoak dira, piramidalak zehazki. Zenbaki piramidalak zenbaki karratuen batura gisa lortzen dira. Pentsatu honelako piramide batean: oinarrian, 6×6 (36) bola ditu; horren ginean, eta behekoen tartean, 5×5 (25) bola daude; hurrengo solairuan, 4×4 (16) bola aurrekoen tartean ere; ondoren, 3×3 (9) bola egongo dira; azkenaurrekoan, 2×2 (4) bola izango ditugu; eta goiko erpinean, 1×1 (1) bola bakarra; guztira, 1 + 4 + 9 + 16 + 25 + 36 = 91 bola. Antzeko eran osatuko genuke pieza ilunen piramidea, baina kasu horretan piramide moztu bat erabiltzen da: oinarrian, 8×8 (64) bola ditu; horren ginean, eta behekoen tartean, 7×7 (49) bola daude; hurrengo solairuan, 6×6 (36) bola aurrekoen tartean ere; ondoren, 5×5 (25) bola egongo dira; eta azkenean, 4×4 (16) bola izango ditugu; guztira, 16 + 25 + 36 + 49 + 64 = 190 bola.
Bi bitxikeria aipatuko ditugu: jokalariek zenbaki berdin batzuk dauzkate haien piezetan, 9, 16, 25, 36, 49, 64 eta 81, 3 eta 9 arteko zenbakien karratuak. Jokalari baten hasierako piezak bakoitiak eta bestearenak bikoitiak badira ere, bukaeran, bi jokalariek pieza bakoitiak adina pieza bikoitiak dituzte.
Ritmomakiaren harrapaketen matematika
Harrapaketetan berdintza eta eragiketa aritmetikoak agertzen dira. Hortaz, piezen balioak ezagutuz eta harrapaketa mota bakoitzean egin behar den eragiketa kontuan hartuz, aldez aurretik jakin daiteke zer pieza erabil daitekeen aurkariaren pieza bat harrapatzeko. Ez da harritzekoa, beraz, testu-egileek beren taulak ematea lan hori errazteko.
Piramideei dagokienez, piramideak osorik edo piezaka erabil daitezke harrapatzeko, eta bi eratara izan daitezke erasoak. Bi aukerak hartuko ditugu kontuan. Guk piramideen piezak ere kontuan izan ditugu; horrela, piramide argiaren 1eko zirkulua ikus daiteke zerrendetan, 1 (p) moduan adierazita. Piramideen gainerako piezen balioa errepikaturik daudenez pieza arruntetan, ez dira tauletan bereizten. Piramideei dagozkien taulak ez ditugu jarri, baina ondorioak bai jarriko ditugu.
Honela egingo dugu prozesua. Lehendabizi, piezen zenbakizko balioak besterik ez dugu kontuan hartuko. Hau da, ez dugu jakingo zenbakizko balio hori daraman pieza karratua, triangelua edo zirkulua den. Pieza argiak eta ilunak, aldiz, bereiziko ditugu, jakiteko jokalari bakoitzak zer aukera dituen harrapaketak egiteko. Bukatzeko, zenbakizko balio batzuk errepikaturik daudenez, harrapatzeko aukerak biderkatzen dira balio bakoitzaren pieza kopuruaz. Hona hemen zenbakizko balioen errepikapenen taula:
| zenbat | piezak | ||||||||
| bost |
25 |
25 |
25 |
25 |
25 |
||||
| lau |
9 |
9 |
9 |
9 |
16 |
16 |
16 |
16 |
|
|
36 |
36 |
36 |
36 |
49 |
49 |
49 |
49 |
||
| hiru |
4 |
4 |
4 |
64 |
64 |
64 |
81 |
81 |
81 |
| bi |
6 |
||||||||
| bat |
1 |
2 |
3 |
5 |
7 |
8 |
12 |
15 |
20 |
|
28 |
30 |
42 |
45 |
56 |
66 |
72 |
90 |
91* |
|
|
100 |
120 |
121 |
153 |
169 |
190* |
225 |
289 |
361 |
|
Topoz egindako harrapaketan, aurkariaren pieza bat harrapatzeko baldintza balio bereko pieza batekin harrapatzea da. Hortaz, bi aldeetan dauden balio bereko piezak baino ezin dira harrapatu. Taula hau, beraz, erraz osa dezakegu. Piramideak osatzen dituzte piezak ere hartu ditugu kontuan; azpian pieza kopuruak daude, kolore eta balio bakoitzeko.
|
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
|
Argiak |
triangelua / piramidea (t) |
zirkulua / piramidea (t) |
triangelua / karratua / piramidea (k) |
zirkulua / piramidea (k) |
triangelua |
zirkulua |
triangelua / karratua |
|
13 |
2 |
2 |
3 |
2 |
1 |
1 |
2 |
|
Ilunak |
zirkuluak |
triangelua / piramidea (z) |
zirkulua / piramidea (t) |
triangelua / piramidea (t) |
zirkulua / karratua / piramidea (k) |
triangelua / piramidea (k) |
zirkulua |
|
14 |
2 |
2 |
2 |
2 |
3 |
2 |
1 |
Piezen itxurak kontuan hartuz, guztira, 25 aukera daude harrapaketak egiteko. Taula honetan zenbaki bakoitzak harrapaketa gauzatzeko dituen aukerak ikus daitezke:
|
piezak |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
|
aukerak |
4 |
4 |
6 |
4 |
3 |
2 |
2 |
25 |
|
piezak |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
Ikus daitekeenez, 25 zenbakiak aukera gehien du harrapaketak egiteko; izan ere, hiru pieza argik eta bi ilunek dute 25 balioa.
Erasoz egindako harrapaketan biderketa eta zatiketa sartzen dira. Biderketan, faktore bat piezaren balioa da eta bestea laukien kopurua; taula osatzeko, piezen arteko lauki hutsak hartu ditugu kontuan. Taularen zabalera 16 denez, bi piezaren arteko distantzia handiena 14 da. 1(p) pieza piramide argian dagoen zirkulua da, eta * marka dutenak piramideak dira. Hona hemen taula:
|
Pieza argia |
× |
ilunaren kontra |
Pieza iluna |
× |
argiaren kontra |
|
piezaren balioa |
lauki kopurua |
piezaren balioa |
piezaren balioa |
lauki kopurua |
piezaren balioa |
|
1 (p)
|
3 |
3 |
3
|
2 |
6 |
|
5 |
5 |
3 |
9 |
||
|
7 |
7 |
5 |
15 |
||
|
9 |
9 |
12 |
36 |
||
|
12 |
12 |
14 |
42 |
||
|
2
|
6 |
12 |
5
|
3 |
15 |
|
8 |
16 |
4 |
20 |
||
|
14 |
28 |
5 |
25 |
||
|
4
|
3 |
12 |
9 |
45 |
|
|
4 |
16 |
7
|
6 |
42 |
|
|
7 |
28 |
7 |
49 |
||
|
9 |
36 |
13 |
91* |
||
|
14 |
56 |
9
|
1 |
9 |
|
|
6
|
2 |
12 |
4 |
36 |
|
|
5 |
30 |
5 |
45 |
||
|
6 |
36 |
8 |
72 |
||
|
11 |
66 |
9 |
81 |
||
|
8
|
2 |
16 |
12
|
3 |
36 |
|
7 |
56 |
6 |
72 |
||
|
8 |
64 |
16
|
1 |
16 |
|
|
9
|
1 |
9 |
4 |
64 |
|
|
4 |
36 |
25 |
1 |
25 |
|
|
9 |
81 |
36
|
1 |
36 |
|
|
10 |
90 |
2 |
72 |
||
|
15
|
2 |
30 |
49 |
1 |
49 |
|
6 |
90 |
64 |
1 |
64 |
|
|
8 |
120 |
81 |
1 |
81 |
|
|
16
|
1 |
16 |
|
|
|
|
4 |
64 |
|
|
|
|
|
20
|
5 |
100 |
|
|
|
|
6 |
120 |
|
|
|
|
|
25
|
1 |
25 |
|
|
|
|
4 |
100 |
|
|
|
|
|
9 |
225 |
|
|
|
|
|
36 |
1 |
36 |
|
|
|
|
45
|
2 |
90 |
|
|
|
|
5 |
225 |
|
|
|
|
|
49 |
1 |
49 |
|
|
|
|
64 |
1 |
64 |
|
|
|
|
81 |
1 |
81 |
|
|
|
|
15 pieza desberdin |
|
19 pieza desberdin |
11 pieza desberdin |
|
14 pieza desberdin |
Taula horretan oinarriturik eta piezek duten itxura desberdinak kontuan hartuz, datu hauek atera ditugu:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
5 |
3 |
15 |
8 |
3 |
8 |
3 |
4 |
2 |
9 |
2 |
|
2 |
1 |
1 |
|
2 |
|
|
|
|
|
68 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
5 |
4 |
3 |
10 |
2 |
4 |
2 |
|
|
4 |
3 |
|
2 |
|
1 |
|
|
|
|
|
|
|
40 |
Honela irakurriko dugu taula: 4 zenbakia hiru pieza argitan dago (piramidearen 4ko zirkulua kontuan hartuz) eta 4 zenbakiarekin 5 eraso egin daitezke, gaineko taulan agertzen den bezala; hortaz, 4 zenbakia duten pieza argiek 15 harrapaketa egin ditzakete.
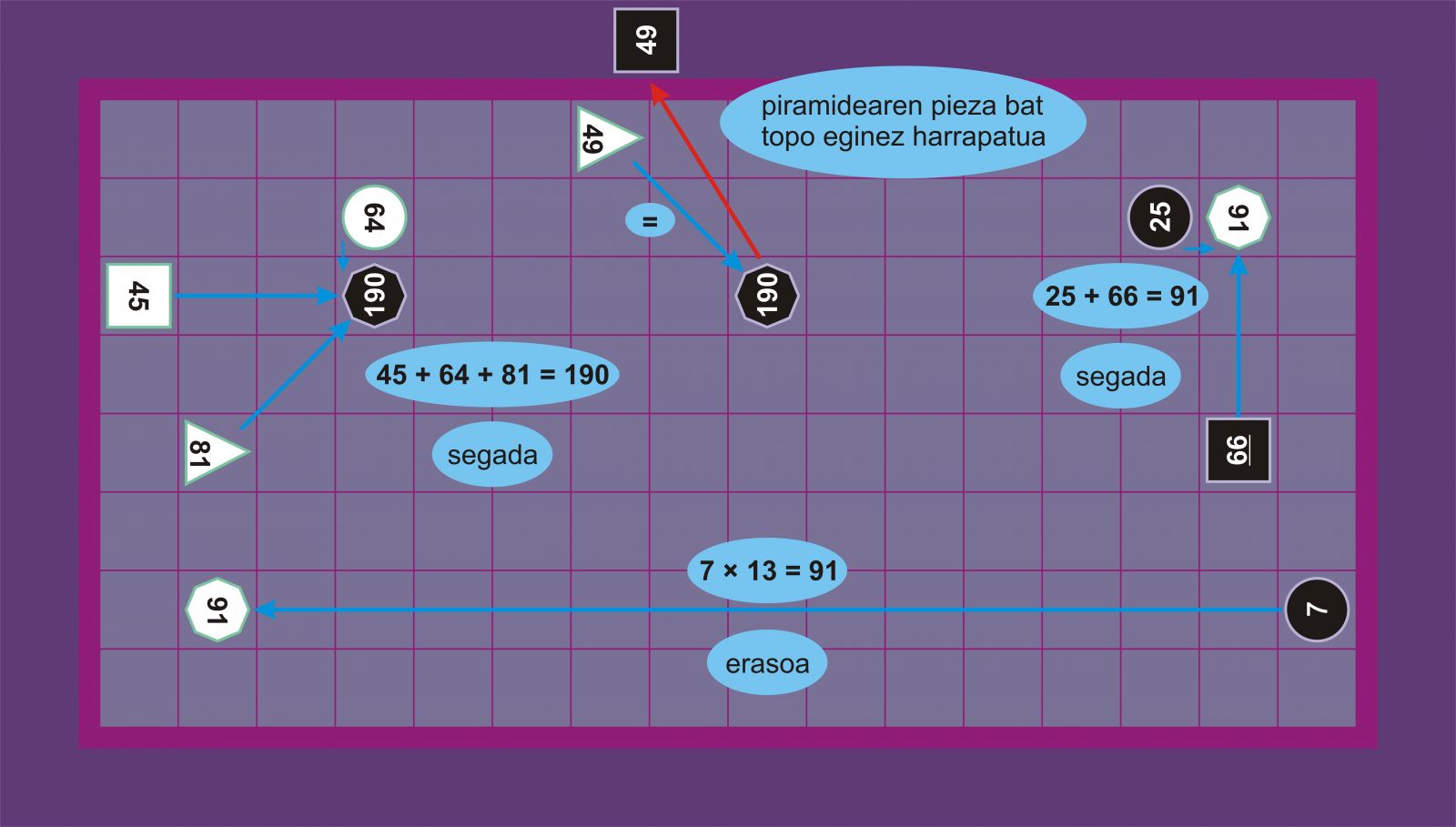
Taulatik ondoriozta daiteke pieza argiek abantailatxo bat dutela, pieza gehiago erabil daitezkeelako ilunak harrapatzeko eta pieza gutxiago izan daitezkeelako harrapatuak. Pieza argien 1(p), 2, 4, 8, 153, 169 eta 289 ezin dira bide honetatik harrapatu. Pieza ilunen 121, 190* eta 361 ezin dira bide honetatik harrapatu. Azpimarratzekoa da piramide argia harrapa daitekeela, 7 × 13 = 91*, baina piramide iluna ez.
Piramide argiak ezin du mota honetako harrapaketarik egin; piramide argiaren piezekin, ordea, 14 pieza ilun harrapa daitezke, 4 piramide ilunean. Alderantziz, piramide argi osoa (7×13 = 91*) eta haren hiru pieza izan daitezke harrapatuak. Bestalde, piramide ilunak ere ezin du honelako harrapaketarik egin; eta horren piezek, ordea, 6 pieza argi harrapa ditzakete, 3 piramide argian. Alderantziz, piramide osoa ezin da harrapatu, baina haren bost piezak bai.
Zatiketan, zatikizuna piezaren balioa da eta zatitzailea laukien kopurua; taula osatzeko, piezen arteko lauki hutsak hartu ditugu kontuan. Taularen zabalera 16 denez, bi piezaren arteko distantzia handiena 14 da. Hona hemen taula:
|
Pieza argia |
/ |
ilunaren kontra |
Pieza iluna |
/ |
argiaren kontra |
|
piezaren balioa |
lauki kopurua |
piezaren balioa |
piezaren balioa |
lauki kopurua |
piezaren balioa |
|
6 |
2 |
3 |
3 |
3 |
1 (p) |
|
9
|
1 |
9 |
5 |
5 |
1 (p) |
|
3 |
3 |
7 |
7 |
1 (p) |
|
|
15
|
3 |
5 |
9
|
1 |
9 |
|
5 |
3 |
9 |
1 (p) |
||
|
16 |
1 |
16 |
12
|
2 |
6 |
|
20 |
4 |
5 |
3 |
4 |
|
|
25
|
1 |
25 |
6 |
2 |
|
|
5 |
5 |
12 |
1 (p) |
||
|
36
|
1 |
36 |
16
|
1 |
16 |
|
3 |
12 |
2 |
8 |
||
|
4 |
9 |
4 |
4 |
||
|
12 |
3 |
8 |
2 |
||
|
42 |
6 |
7 |
25 |
1 |
25 |
|
45
|
5 |
9 |
28
|
7 |
4 |
|
9 |
5 |
14 |
2 |
||
|
49
|
1 |
49 |
30
|
2 |
15 |
|
7 |
7 |
5 |
6 |
||
|
64
|
1 |
64 |
36
|
1 |
36 |
|
4 |
16 |
4 |
9 |
||
|
72
|
2 |
36 |
6 |
6 |
|
|
6 |
12 |
9 |
4 |
||
|
8 |
9 |
49 |
1 |
49 |
|
|
81
|
1 |
81 |
56
|
7 |
8 |
|
9 |
9 |
14 |
4 |
||
|
91* |
13 |
7 |
64
|
1 |
64 |
|
|
|
|
4 |
16 |
|
|
|
|
|
8 |
8 |
|
|
|
|
|
66 |
11 |
6 |
|
|
|
|
81
|
1 |
81 |
|
|
|
|
9 |
9 |
|
|
|
|
|
90
|
2 |
45 |
|
|
|
|
6 |
15 |
|
|
|
|
|
10 |
9 |
|
|
|
|
|
100
|
4 |
25 |
|
|
|
|
5 |
20 |
|
|
|
|
|
120
|
6 |
20 |
|
|
|
|
8 |
15 |
|
|
|
|
|
225
|
5 |
45 |
|
|
|
|
9 |
25 |
|
|
14 pieza desberdin |
|
11 pieza desberdin |
19 pieza desberdin |
|
15 pieza desberdin |
Taula horretan oinarriturik eta piezek duten itxura desberdinak kontuan hartuz, datu hauek atera ditugu:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
|
|
2 |
|
4 |
2 |
2 |
1 |
6 |
8 |
1 |
2 |
2 |
2 |
3 |
4 |
1 |
|
|
|
|
40 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
1 |
1 |
1 |
4 |
4 |
8 |
2 |
2 |
2 |
8 |
3 |
2 |
6 |
1 |
2 |
3 |
2 |
2 |
|
|
2 |
|
56 |
Gorago bezala irakurriko dugu taula: 16 zenbakia bi pieza argitan dago (piramidearen 16ko zirkulua kontuan hartuz) eta 16 zenbakiarekin 4 eraso egin daitezke, gaineko taulan agertzen den bezala; hortaz, 16 zenbakia duten pieza ilunek 8 harrapaketa egin ditzakete.
Taulatik ondorioztatzen dugu pieza ilunek abantailatxo bat dutela, pieza gehiago erabil daitezkeelako argiak harrapatzeko eta pieza gutxiago izan daitezke harrapatuak. Pieza argien 42, 72, 91*, 153, 169 eta 289 ezin dira bide honetatik harrapatu. Pieza ilunen 28, 30, 56, 66, 90, 100, 120, 121, 190*, 225 eta 361 ezin dira bide honetatik harrapatu.
Piramide argiak 7ko zirkulu iluna harrapa dezake (91*/13 = 7); piramide argiaren piezekin, ordea, 7 pieza ilun harrapa daitezke, 3 piramide ilunean. Alderantziz, piramide argi osoa ezin da harrapatu, eta, 1eko zirkulua izan ezik, haren gainerako piezak izan daitezke harrapatuak. Bestalde, piramide ilunak ere ezin du honelako harrapaketarik egin; eta horren piezek, ordea, 10 pieza argi harrapa ditzakete, 5 piramide argian. Alderantziz, piramide osoa ezin da harrapatu, baina haren bost piezak bai.
Segadaz egindako harrapaketan batuketa eta kenketa sartzen dira. Testu batzuetan, batuketan, bi pieza baino gehiago erabil daitezke pieza bat harrapatzeko. Guk, hemen, bi piezaren kasua soilik emango dugu. Bi piezaren balioak batuko ditugu aurkariaren pieza baten balioa lortzeko. 1(p) pieza piramide argian dagoen zirkulua da. Hona hemen taula:
|
Bi pieza argi |
ilunaren kontra |
Bi pieza ilun |
argiaren kontra |
||
|
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
|
1 (p)
|
2 |
3 |
3
|
5 |
8 |
|
4 |
5 |
12 |
15 |
||
|
6 |
7 |
7 |
9 |
16 |
|
|
8 |
9 |
9
|
16 |
25 |
|
|
15 |
16 |
36 |
45 |
||
|
2 |
64 |
66 |
12 |
30 |
42 |
|
4
|
8 |
12 |
16 |
56 |
72 |
|
45 |
49 |
25
|
56 |
81 |
|
|
6 |
6 |
12 |
66 |
91* |
|
|
8 |
20 |
28 |
28 |
36 |
64 |
|
9
|
16 |
25 |
36 |
36 |
72 |
|
72 |
81 |
49 |
120 |
169 |
|
|
81 |
90 |
64 |
225 |
289 |
|
|
91* |
100 |
|
|
|
|
|
15 |
49 |
64 |
|
|
|
|
16 |
20 |
36 |
|
|
|
|
20 |
36 |
56 |
|
|
|
|
36
|
45 |
81 |
|
|
|
|
64 |
100 |
|
|
|
|
|
49 |
72 |
121 |
|
|
|
|
72
|
153 |
225 |
|
|
|
|
289 |
361 |
|
|
|
|
|
12 pieza desberdin |
16 pieza desberdin |
19 pieza desberdin |
10 pieza desberdin |
10 pieza desberdin |
12 pieza desberdin |
|
guztira, 18 pieza desberdin |
|
guztira, 16 pieza desberdin |
|
||
Zenbakiak errepikatzen direnez hainbat piezatan, goiko aukerak honela banatzen dira zenbakien arabera:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
7 |
2 |
8 |
3 |
4 |
10 |
2 |
5 |
5 |
|
6 |
|
4 |
2 |
3 |
5 |
4 |
1 |
1 |
|
1 |
|
73 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
2 |
1 |
2 |
10 |
2 |
6 |
4 |
2 |
1 |
7 |
3 |
4 |
2 |
2 |
|
|
|
3 |
|
|
2 |
|
53 |
Eta honela irakurriko dugu: bi pieza argik dute 9 balioa, bi triangelu hain zuzen, horietako bat piramidean. Piramidean ez dagoen 9koa sei piezaren balioekin (16, 16, 72, 81, 81 eta 91*) batu daiteke pieza ilun baten balioa lortzeko; piramidearen 9koa, ordea, lau piezaren balioekin (16, 72, 81 eta 81) batu daiteke helburu berarekin. Guztira, 9ko pieza argiek 10 aukera dute pieza ilun bat harrapatzeko.
Taulatik ondoriozta daiteke pieza argiek abantailatxo bat dutela, pieza gehiago erabil daitekeelako ilunak harrapatzeko eta pieza gutxiago izan daitezke harrapatuak. Pieza argien 1, 2, 4, 6, 9, 20, 36, 49 eta 153 ezin dira bide honetatik harrapatu. Pieza ilunen 30, 120 eta 190* ezin dira bide honetatik harrapatu.
Piramide argi osoak, 9ko triangelu argiarekin, 100ko triangelu iluna harrapa dezake (91*+9 = 100); piramide argiaren piezekin, aldiz, 12 pieza ilun harrapa daitezke, 5 piramide ilunean. Alderantziz, piramide argi osoa harrapatua izan daiteke (25+66 = 91*), eta, 25eko karratua izan ezik, haren gainerako piezak ezin daitezke harrapatu. Bestalde, piramide ilunak ezin du honelako harrapaketarik egin; eta horren piezek, ordea, piramide argi osoa (25+66 = 91*) eta 7 pieza argi harrapa ditzakete, 1 piramide argian. Alderantziz, piramide osoa ezin da harrapatu, baina haren bost piezak bai.
Kenketan, bi pieza baino ezin dira erabili. Kenkizuna pieza baten balioa da, eta kentzailea beste batena. Zutabeak kenkizun handienetik txikienera antolatuko ditugu. Hona hemen taula:
|
Bi pieza argi |
ilunaren kontra |
Bi pieza ilun |
argiaren kontra |
||
|
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
piezaren balioa |
|
289
|
169 |
120 |
225 |
56 |
169 |
|
64 |
225 |
121
|
120 |
1 (p) |
|
|
169
|
153 |
16 |
49 |
72 |
|
|
49 |
120 |
30 |
91* |
||
|
153 |
72 |
81 |
120
|
100 |
20 |
|
91*
|
42 |
49 |
56 |
64 |
|
|
25 |
66 |
100
|
64 |
36 |
|
|
81
|
72 |
9 |
36 |
64 |
|
|
45 |
36 |
28 |
72 |
||
|
25 |
56 |
9 |
91* |
||
|
15 |
66 |
90
|
81 |
9 |
|
|
72
|
42 |
30 |
9 |
81 |
|
|
36 |
36 |
81
|
66 |
15 |
|
|
16 |
56 |
56 |
25 |
||
|
8 |
64 |
36 |
45 |
||
|
6 |
66 |
9 |
72 |
||
|
64
|
36 |
28 |
66
|
64 |
2 |
|
15 |
49 |
30 |
36 |
||
|
49 |
42 |
7 |
64
|
56 |
8 |
|
45
|
42 |
3 |
49 |
15 |
|
|
36 |
9 |
28 |
36 |
||
|
20 |
25 |
56
|
36 |
20 |
|
|
15 |
30 |
7 |
49 |
||
|
9 |
36 |
49 |
7 |
42 |
|
|
42 |
6 |
36 |
36
|
30 |
6 |
|
36
|
20 |
16 |
28 |
8 |
|
|
8 |
28 |
16 |
20 |
||
|
6 |
30 |
30
|
28 |
2 |
|
|
25
|
20 |
5 |
5 |
25 |
|
|
16 |
9 |
28
|
12 |
16 |
|
|
9 |
16 |
3 |
25 |
||
|
20
|
15 |
5 |
25
|
16 |
9 |
|
8 |
12 |
9 |
16 |
||
|
4 |
16 |
5 |
20 |
||
|
16
|
9 |
7 |
16
|
12 |
4 |
|
4 |
12 |
7 |
9 |
||
|
15
|
8 |
7 |
12 |
3 |
9 |
|
6 |
9 |
9
|
7 |
2 |
|
|
9
|
6 |
3 |
5 |
4 |
|
|
4 |
5 |
3 |
6 |
||
|
2 |
7 |
7
|
5 |
2 |
|
|
8 |
1 (p) |
7 |
3 |
4 |
|
|
6 |
1 (p) |
5 |
5 |
3 |
2 |
|
4 |
1 (p) |
3 |
|
|
|
|
19 pieza desberdin |
18 pieza desberdin |
18 pieza desberdin |
19 pieza desberdin |
17 pieza desberdin |
19 pieza desberdin |
|
guztira, 21 pieza desberdin |
|
guztira, 20 pieza desberdin |
|
||
Ikus dezagun harrapatzeko aukerak zenbakien arabera:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
5 |
2 |
15 |
16 |
6 |
21 |
8 |
14 |
11 |
21 |
14 |
7 |
10 |
2 |
4 |
11 |
12 |
3 |
2 |
3 |
2 |
|
189 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
6 |
7 |
10 |
16 |
4 |
10 |
9 |
8 |
6 |
13 |
11 |
8 |
13 |
4 |
7 |
3 |
8 |
3 |
5 |
|
1 |
|
152 |
Hona hemen irakurketa: 9a bi pieza ilunetan dago, biak piramidetik at, beraz biek aukera kopuru bera dute pieza ilunak harrapatzeko. Gaineko taulan 9a hiru aldiz agertzen da kenkizun gisa eta lau kentzaile gisa. Kenkizuna hiru piezaren balioekin (7, 5, 3) eragiten da, guztira, sei aukera emanez; kentzailea bost piezaren balioekin (100, 90, 81, 25, 25) eragiten da, guztira, hamar aukera emanez.
Kasu honetan, taulak indarrak parekatuagoak daudela esaten digu. Pieza argien 153 eta 289 ezin dira bide honetatik harrapatu. Pieza ilunen 100, 121, 190* eta 361 ezin dira bide honetatik harrapatu.
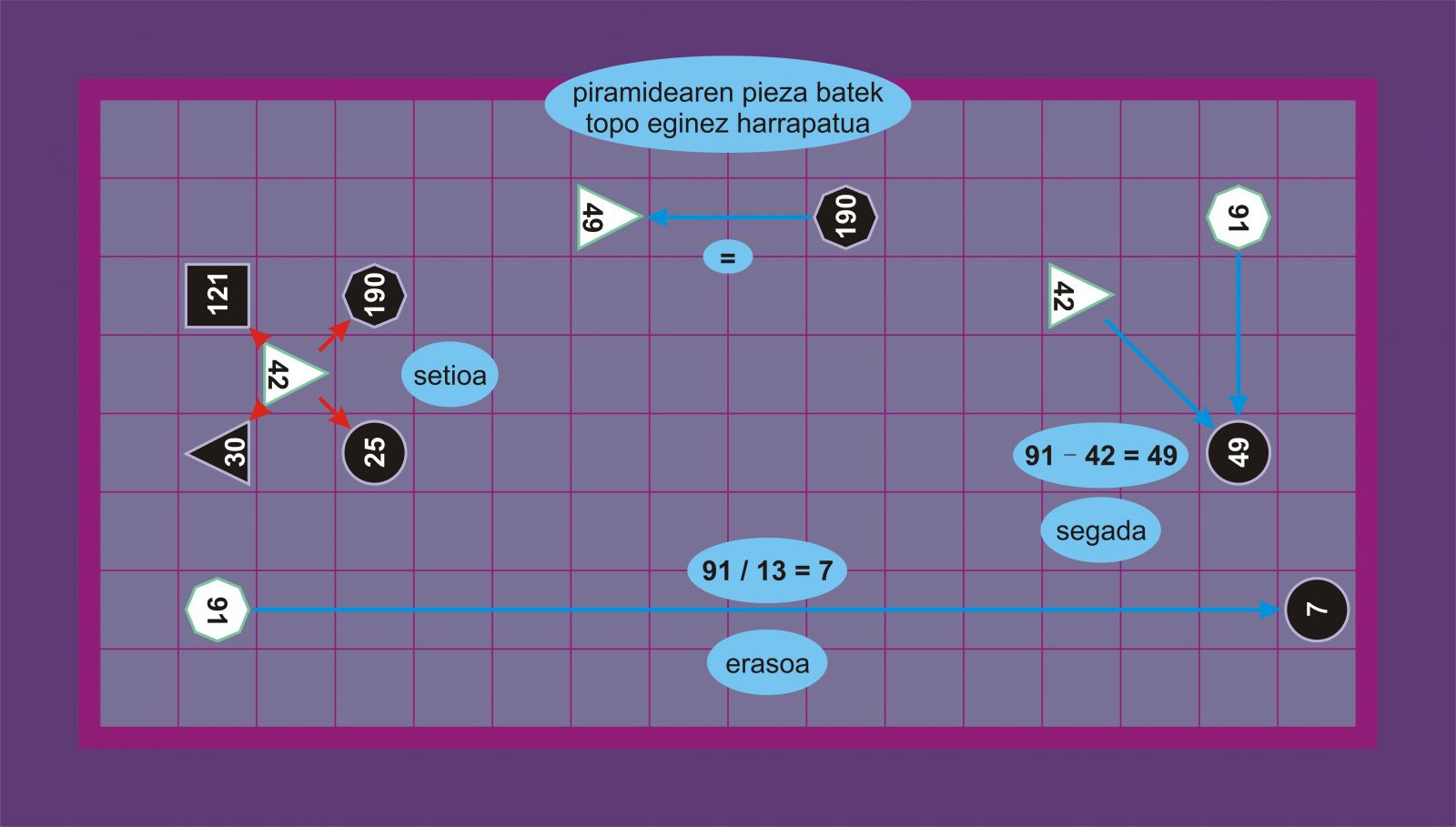
Piramide argi osoak, 42ko triangelu argiarekin, 49ko pieza ilunak harrapa ditzake (91* – 42 = 49) eta, 25eko pieza argiekin, 66ko karratu iluna harrapa dezake (91* – 25 = 66); horrez gain, piramide argiaren piezekin 10 pieza ilun harrapa daitezke, 2 piramide ilunean. Alderantziz, piramide argi osoa bi eratan harrapa daiteke (121 – 30 = 91* eta 100 – 9 = 91*) eta haren sei piezak ere harrapa daitezke. Bestalde, piramide ilunak ezin du honelako harrapaketarik egin; eta horren piezek, ordea, 13 pieza argi harrapa ditzakete, 4 piramide argian. Alderantziz, piramide osoa ezin da harrapatu, baina haren bost piezak bai.
Setioan ez dira eragiketak erabiltzen.
Hurrengo tauletan laburtuko dugu piezen erasotzeko ahalmena. Taula hauetan agertzen diren kopuruek adierazten dute piezen balio bakoitzak zenbat erasotan har dezakeen parte. Balio horiek aurreko taula guztietatik atera ditugu. Azkeneko errenkadan eta zutabean baturak daude.
|
|
|
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
Topoz |
= |
|
|
|
|
|
4 |
|
4 |
|
6 |
4 |
|
|
3 |
2 |
|
2 |
|
|
|
|
25 |
|
Erasoa
|
× |
5 |
3 |
15 |
8 |
3 |
8 |
3 |
4 |
2 |
9 |
2 |
|
2 |
1 |
1 |
|
2 |
|
|
|
|
68 |
|
/ |
|
|
|
2 |
|
4 |
2 |
2 |
1 |
6 |
8 |
1 |
2 |
2 |
2 |
3 |
4 |
1 |
|
|
|
40 |
|
|
Segada
|
+ |
7 |
2 |
8 |
3 |
4 |
10 |
2 |
5 |
5 |
|
6 |
|
4 |
2 |
3 |
5 |
4 |
1 |
1 |
|
1 |
73 |
|
- |
5 |
2 |
15 |
16 |
6 |
21 |
8 |
14 |
11 |
21 |
14 |
7 |
10 |
2 |
4 |
11 |
12 |
3 |
2 |
3 |
2 |
189 |
|
|
|
|
17 |
7 |
38 |
29 |
13 |
47 |
15 |
29 |
19 |
42 |
34 |
8 |
18 |
10 |
12 |
19 |
24 |
5 |
3 |
3 |
3 |
395 |
|
|
|
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
Topoz |
= |
|
|
|
4 |
|
4 |
6 |
|
|
4 |
3 |
|
2 |
|
2 |
|
|
|
|
|
|
|
25 |
|
Erasoa
|
× |
5 |
4 |
3 |
10 |
2 |
4 |
2 |
|
|
4 |
3 |
|
2 |
|
1 |
|
|
|
|
|
|
|
40 |
|
/ |
1 |
1 |
1 |
4 |
4 |
8 |
2 |
2 |
2 |
8 |
3 |
2 |
6 |
1 |
2 |
3 |
2 |
2 |
|
|
2 |
|
56 |
|
|
Segada
|
+ |
2 |
1 |
2 |
10 |
2 |
6 |
4 |
2 |
1 |
7 |
3 |
4 |
2 |
2 |
|
|
|
3 |
|
|
2 |
|
53 |
|
- |
6 |
7 |
10 |
16 |
4 |
10 |
9 |
8 |
6 |
13 |
11 |
8 |
13 |
4 |
7 |
3 |
8 |
3 |
5 |
|
1 |
|
152 |
|
|
|
|
14 |
13 |
16 |
44 |
12 |
32 |
23 |
12 |
9 |
36 |
23 |
14 |
25 |
7 |
12 |
6 |
10 |
8 |
5 |
0 |
5 |
0 |
326 |
Pieza argietan ikusten da erasorako ahalmen gehien 9ko piezek dutela, 25ko piezak oso urrun ez dituztela. Pieza ilunetan 9ko piezak ere dira ahaltsuenak, alde gehiagorekin. Tauletan ere ikusten da piramideek ez dutela garrantzia handirik harrapaketetan, argiak bost kasutan baino ez du parte hartzen, eta ilunak batean ere ez.
Aipatzekoa da, segadan, kenketak aukera gehiago sortzen dituela bai pieza argiekin bai pieza ilunekin. Eta pieza ilunei hobeto datorkie zatiketa eta kenketa harrapaketak egiteko.
Oro har, bi taulak erkatuz, ongi ikusten da pieza argiak erasokorragoak direla; argiek 395 aukera dituzte eraso egiteko, eta ilunek 326.
Ritmomakiaren garaipenen matematika
Ritmomakiaren helburu nagusia berariazko garaipena lortzea da, garaipen arruntak ere helburu gisa har badaitezke ere, hasiberrientzat gehienbat. Garaipen arruntetan bost dira irabazteko ados daitezkeen bideak: 1-harrapatutako pieza kopurua, 2-harrapatutako piezen balioen batura, 3-harrapatutako piezetan dauden zifra kopurua, 4-harrapatutako pieza kopuru jakin batekin piezen balioen batura eta 5-harrapatutako pieza kopuru jakin batekin eta piezen zifra kopuru jakin batekin piezen balioen batura.
Berariazko garaipenetan, aldiz, harmoniak dira garrantzitsuak. Harmonia horiek progresio aritmetikoa, progresio geometrikoa eta progresio harmonikoa dira. Har ditzagun 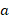 ,
, 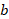 ,
, 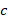 zenbakiak: progresio aritmetikoa osatzen dute
zenbakiak: progresio aritmetikoa osatzen dute 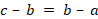 betetzen bada; progresio geometrikoa osatzen dute
betetzen bada; progresio geometrikoa osatzen dute 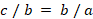 betetzen bada; progresio harmonikoa osatzen dute
betetzen bada; progresio harmonikoa osatzen dute 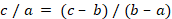 betetzen bada. Progresioen izenak lotuta daude bi zenbakiren batezbesteko aritmetiko, geometriko eta harmonikoarekin. Izan ere, progresio aritmetikoan,
betetzen bada. Progresioen izenak lotuta daude bi zenbakiren batezbesteko aritmetiko, geometriko eta harmonikoarekin. Izan ere, progresio aritmetikoan, 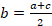 da, batezbesteko aritmetikoa; progresio geometrikoan,
da, batezbesteko aritmetikoa; progresio geometrikoan, 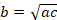 da, batezbesteko geometrikoa; eta progresio harmonikoan,
da, batezbesteko geometrikoa; eta progresio harmonikoan, 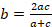 da, batezbesteko harmonikoa.
da, batezbesteko harmonikoa.
Hiru progresioetan kasu nabaria gertatzen da hiru zenbakiak zenbaki bera direnean; esate baterako, 9-9-9 progresio aritmetikoa, geometrikoa eta harmonikoa da. Ritmomakian, beraz, balio bereko hiru pieza beharko genituzke horrelako kasu nabaria osatzeko. Piramideen piezak kontuan hartu gabe, badira pieza kopuru hori duten balioak, baina ez jokalari baten eskuan, bi jokalarien piezak erabiliz baizik: 9, 25, 49 eta 81. Piramideen piezak kontuan hartuz gero, balio horiez gain, 4, 16, 36 eta 64 balioek ere osa dezakete progresio nabaria. Bi kasutan, 4 eta 25, kolore argiko piezekin osa daiteke progresio nabaria; pieza ilunen 49 balioarekin ere osa daiteke horrelako bat. Jokoari begira, erabaki beharko litzateke horrelako progresio nabariak onartzen diren edo ez.
Aurreko guztia jakinda eta jokalarien piezetan agertzen diren balioak ezaguturik, progresio horiek osatzen dituzten piezen taulak osa daitezke. Progresioetan piramide osoak, 91* eta 190*, eta piramideetan dauden piezak ere kontuan hartu ditugu (horrek 1ekoari baino ez dio eragiten, gainerako piezak errepikaturik daudelako piramideetatik at). Jokalarien esku geratuko da piramide osoak edota piramideen piezak progresioak osatzeko onartzea edo ez.
Tauletan piezen zenbakizko balioen konbinazioak emango ditugu, zer aldetan dauden edo zer itxura duten kontuan hartu gabe. Jokalarien aukerak emateko orduan, piezen itxura, pieza errepikatuak eta haien artean nahasteko aukerak hartuko ditugu kontuan. Taulak bi multzotan emango ditugu, kolore bateko konbinazioekin eta konbinazio nahasiekin, jokalariek jakin dezaten zer aukera duten beren piezekin progresioak osatzeko, baita aurkariaren piezekin progresioak osatzeko ere. Hondo zuriko laukietan bi jokalariek dituzten piezak dira (9, 16, 25, 36, 49, 64 eta 81). Kontuz ibili behar da aukera desberdinak zenbatzerakoan konbinazio nahasietan; izan ere, konbinazio nahasiak direnez, konbinazioetan pieza argiak eta ilunak daudela bermatu behar da.
Hala moduzko garaipenak
Kasu honetan, hiru piezarekin progresio aritmetiko, progresio geometriko edo progresio harmoniko bat osatu behar dute jokalariek.
Progresio aritmetikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
||||||||||||||
|
1 |
8 |
15 |
3 |
5 |
7 |
1 |
2 |
3 |
4 |
8 |
12 |
12 |
16 |
20 |
||
|
1 |
25 |
49 |
5 |
7 |
9 |
1 |
3 |
5 |
4 |
12 |
20 |
12 |
20 |
28 |
||
|
2 |
4 |
6 |
7 |
16 |
25 |
1 |
4 |
7 |
4 |
16 |
28 |
12 |
42 |
72 |
||
|
2 |
9 |
16 |
7 |
28 |
49 |
1 |
5 |
9 |
4 |
30 |
56 |
15 |
30 |
45 |
||
|
4 |
6 |
8 |
7 |
64 |
121 |
1 |
25 |
49 |
5 |
6 |
7 |
15 |
120 |
225 |
||
|
4 |
20 |
36 |
12 |
56 |
100 |
2 |
3 |
4 |
5 |
15 |
25 |
20 |
25 |
30 |
||
|
8 |
25 |
42 |
12 |
66 |
120 |
2 |
5 |
8 |
5 |
25 |
45 |
20 |
28 |
36 |
||
|
8 |
36 |
64 |
16 |
36 |
56 |
2 |
7 |
12 |
6 |
7 |
8 |
28 |
42 |
56 |
||
|
9 |
45 |
81 |
28 |
64 |
100 |
2 |
9 |
16 |
6 |
9 |
12 |
30 |
36 |
42 |
||
|
9 |
81 |
153 |
|
|
|
2 |
15 |
28 |
6 |
36 |
66 |
42 |
49 |
56 |
||
|
15 |
20 |
25 |
|
|
|
2 |
16 |
30 |
7 |
8 |
9 |
42 |
66 |
90 |
||
|
20 |
42 |
64 |
|
|
|
3 |
4 |
5 |
7 |
49 |
91* |
42 |
81 |
120 |
||
|
49 |
169 |
289 |
|
|
|
3 |
6 |
9 |
8 |
12 |
16 |
56 |
64 |
72 |
||
|
|
|
|
|
|
|
3 |
9 |
15 |
8 |
49 |
90 |
72 |
81 |
90 |
||
|
|
|
|
|
|
|
3 |
42 |
81 |
8 |
64 |
120 |
81 |
153 |
225 |
||
|
|
|
|
|
|
|
4 |
5 |
6 |
9 |
12 |
15 |
91* |
190* |
289 |
||
|
13 progresio aritmetiko |
9 progresio aritmetiko |
48 progresio aritmetiko |
||||||||||||||
Konbinazio horiek honela banatzen dira, gorago esandako irizpideen arabera, hau da, piezen itxura desberdinak kontuan hartuz:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
23 |
32 |
51 |
46 |
33 |
30 |
20 |
18 |
26 |
23 |
15 |
21 |
10 |
8 |
5 |
7 |
16 |
5 |
7 |
1 |
2 |
|
399 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
24 |
29 |
26 |
26 |
31 |
26 |
16 |
23 |
17 |
11 |
23 |
15 |
8 |
10 |
4 |
8 |
3 |
8 |
2 |
1 |
4 |
|
315 |
Honela kalkulatu ditugu kopuru horiek (adibide gisa 49 balio argiaren zortzi aukerak azalduko ditugu): 49 balioa pieza argien bi konbinaziotan ageri da, 1-25-49 eta 49-169-289. Lehenengo konbinazioak 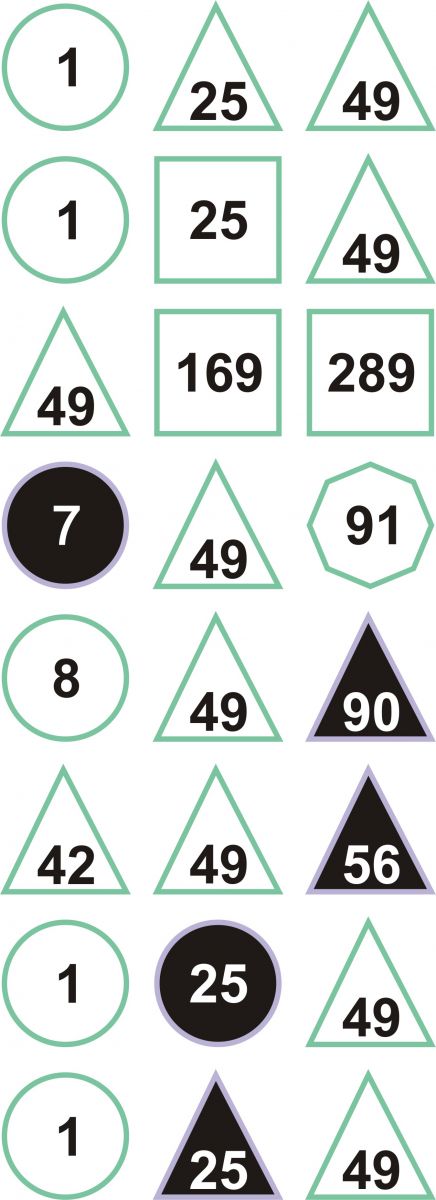 bi aukera ematen ditu, 1eko pieza bakarra dago, 25eko hiru pieza daude eta 49ko pieza bakarra dago. 25ekoaren hiru piezetatik bat, piramidearen pieza dena, baztertu behar da, 1ekoa piramidearen pieza delako eta ezin direlako piramidearen bi pieza erabili. Bigarren konbinazioa bakarra da hiru balioak behin baino ez direlako agertzen pieza argietan. Hortaz, guztira hiru aukera daude konbinazio horiek osatzeko.
bi aukera ematen ditu, 1eko pieza bakarra dago, 25eko hiru pieza daude eta 49ko pieza bakarra dago. 25ekoaren hiru piezetatik bat, piramidearen pieza dena, baztertu behar da, 1ekoa piramidearen pieza delako eta ezin direlako piramidearen bi pieza erabili. Bigarren konbinazioa bakarra da hiru balioak behin baino ez direlako agertzen pieza argietan. Hortaz, guztira hiru aukera daude konbinazio horiek osatzeko.
Konbinazio nahasietan, aldiz, lautan ageri da 49 balioa: 1-25-49, 7-49-91*, 8-49-90 eta 42-49-56. Azken hiru konbinazioek aukera bana ematen dute, bertan agertzen diren balioak behin baino ez direlako agertzen pieza argietan; esan behar da, pieza horietako bat piramide osoa dela, 91*. Lehen konbinazioa nahasia bada, 25eko piezak iluna izan behar du, 1eko eta 49ko piezak argiak direlako. Esan bezala, 1eko eta 49ko pieza argiak bakarrak dira eta 25eko bi pieza ilun daude, bat piramidean; hortaz, konbinazio horrek bi aukera ematen ditu. Konbinazio nahasietan, guztira beraz, bost aukera daude.
Orotara, hortaz, 49ko pieza argiak zortzi aukera ditu progresio aritmetiko bat osatzeko.
Hemen ere ikusten da pieza argiek abantailatxo bat dutela aukera gehiago dutelako progresio aritmetikoak osatzeko. Piezen argien artean, gehien erabiliak 4koak eta 6koak dira. Pieza ilunen artean, ordea, 12koa eta 5ekoa dira erabilienak.
Guztira, pieza argiek, 399 aukera biltzen dute progresio aritmetiko bat lortzeko; eta pieza ilunek 315 aukera biltzen dute. Aukera horiek guztiek 238 konbinazio garaile sortzen dituzte 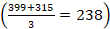 .
.
Progresio geometrikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
||||||
|
1 |
2 |
4 |
9 |
12 |
16 |
1 |
3 |
9 |
|
1 |
4 |
16 |
9 |
30 |
100 |
1 |
4 |
16 |
|
1 |
6 |
36 |
16 |
28 |
49 |
1 |
5 |
25 |
|
1 |
8 |
64 |
16 |
36 |
81 |
1 |
6 |
36 |
|
1 |
9 |
81 |
25 |
30 |
36 |
1 |
7 |
49 |
|
2 |
4 |
8 |
36 |
66 |
121 |
1 |
8 |
64 |
|
4 |
6 |
9 |
36 |
90 |
225 |
1 |
9 |
81 |
|
4 |
8 |
16 |
49 |
56 |
64 |
1 |
15 |
225 |
|
4 |
16 |
64 |
64 |
120 |
225 |
2 |
12 |
72 |
|
9 |
15 |
25 |
81 |
90 |
100 |
3 |
6 |
12 |
|
16 |
20 |
25 |
100 |
190* |
361 |
4 |
12 |
36 |
|
16 |
36 |
81 |
|
|
|
4 |
20 |
100 |
|
25 |
45 |
81 |
|
|
|
4 |
30 |
225 |
|
36 |
42 |
49 |
|
|
|
5 |
15 |
45 |
|
49 |
91* |
169 |
|
|
|
9 |
45 |
225 |
|
64 |
72 |
81 |
|
|
|
16 |
36 |
81 |
|
81 |
153 |
289 |
|
|
|
20 |
30 |
45 |
|
17 progresio geometriko |
11 progresio geometriko |
17 progresio geometriko |
||||||
Hau da konbinazio horiei dagokien aukeren banaketa balioen arabera:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
37 |
6 |
48 |
18 |
11 |
20 |
7 |
38 |
9 |
18 |
30 |
2 |
12 |
4 |
8 |
3 |
44 |
1 |
2 |
1 |
2 |
|
321 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
4 |
5 |
4 |
16 |
18 |
34 |
5 |
5 |
9 |
38 |
13 |
5 |
9 |
2 |
18 |
3 |
7 |
2 |
2 |
1 |
12 |
1 |
213 |
Kopuru horiek gorago azaldutako adibidearen prozesuari jarraituz lortu ditugu. Aukera horiek guztiek 178 konbinazio garaile sortzen dituzte 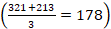 .
.
Berriro ere, argiek abantailatxoa dute eta kasu banatan piramideak erabili direla. Pieza argien artean gehien erabiliak 4, 81 eta 16 dira. Pieza ilunen artean, aldiz, 36 eta 16 dira erabilienak. Piramideak progresio banatan erabiltzen dira.
Esan behar da progresio geometrikoen arrazoia beti ez dela zenbaki osoa; esaterako, bi piramideek osatzen dituzten progresio geometrikoetan, arrazoiak, pieza argien kasuan, 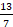 eta, pieza ilunen kasuan,
eta, pieza ilunen kasuan, 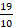 dira.
dira.
Progresio harmonikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
||||||||||||||
|
9 |
15 |
25 |
|
|
|
2 |
3 |
6 |
5 |
9 |
45 |
12 |
15 |
20 |
||
|
9 |
16 |
72 |
|
|
|
3 |
4 |
6 |
6 |
8 |
12 |
15 |
20 |
30 |
||
|
|
|
|
|
|
|
3 |
5 |
15 |
7 |
12 |
42 |
25 |
45 |
225 |
||
|
|
|
|
|
|
|
4 |
6 |
12 |
8 |
15 |
120 |
30 |
36 |
45 |
||
|
|
|
|
|
|
|
4 |
7 |
28 |
9 |
15 |
45 |
30 |
45 |
90 |
||
|
|
|
|
|
|
|
5 |
8 |
20 |
9 |
16 |
72 |
72 |
90 |
120 |
||
|
2 progresio harmoniko |
progresio harmonikorik ez |
18 progresio harmoniko |
||||||||||||||
Lehenengo ondorioa da pieza ilunekin bakarrik ezin dela progresio harmonikorik osatu. Horrek erakusten du harmoniak osatzeko aurkariari harrapatutako piezak erabili ahal izatea zentzuzkoa dela; bestela, pieza ilunek ez zuten aukerarik izango progresio harmonikorik osatzeko.
Goiko taulari dagokion aukeren banaketa hau da:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
2 |
15 |
16 |
4 |
11 |
8 |
7 |
3 |
3 |
2 |
1 |
18 |
|
|
16 |
|
|
|
|
|
|
106 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
9 |
6 |
4 |
12 |
10 |
8 |
2 |
3 |
6 |
2 |
|
|
|
|
|
2 |
|
2 |
|
|
5 |
|
71 |
Nabarmen progresio harmoniko gutxiago osa daitezke eta, beraz, bi aldeek aukera gutxiago dute honela irabazteko. Berez, aukera horiek guztiek 59 konbinazio garaile sortzen dituzte 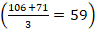 . Oraingoan, 45eko pieza argia eta 9ko pieza iluna dira ahaltsuenak. Piramideak ezin dira erabili progresio harmonikoak lortzeko.
. Oraingoan, 45eko pieza argia eta 9ko pieza iluna dira ahaltsuenak. Piramideak ezin dira erabili progresio harmonikoak lortzeko.
Bukatzeko, piezen balioen konbinazio guztiak, kolore batekoak eta nahasiak, kontuan hartzen baditugu 135 konbinazio osa daitezke. Konbinazio horiek honela banatzen dituzte aukerak balioen arabera:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
60 |
40 |
114 |
80 |
48 |
61 |
35 |
63 |
38 |
44 |
47 |
24 |
40 |
12 |
13 |
26 |
60 |
6 |
9 |
2 |
4 |
|
826 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
37 |
40 |
34 |
54 |
59 |
68 |
23 |
31 |
32 |
51 |
36 |
20 |
17 |
12 |
22 |
13 |
10 |
12 |
4 |
2 |
21 |
1 |
599 |
Pieza argiek 826 aukera dute progresioren bat osatzeko, eta ilunek 599 aukera. Guztira, orduan, hala moduzko garaipen bat lortzeko, 475 konbinazio garaile daude 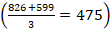 . Horietan gehien erabiltzen diren balioak dira 4a, pieza argietan, eta 16a, pieza ilunetan dira.
. Horietan gehien erabiltzen diren balioak dira 4a, pieza argietan, eta 16a, pieza ilunetan dira.
Garaipen handiak
Kasu honetan, bi progresio osatu behar dituzte jokalariek lau piezarekin: aritmetikoa eta geometrikoa, aritmetikoa eta harmonikoa edo geometrikoa eta harmonikoa.
Berriro ere, hasteko jokalari bakoitzaren piezekin osatutako konbinazioak hartuko ditugu kontuan hasteko. Gogora dezagun lau pieza hartu behar ditugula bi progresioak osatzeko.
Progresio aritmetikoak eta geometrikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
|||||||||||||||||||
|
1 |
2 |
4 |
6 |
7 |
16 |
28 |
49 |
1 |
2 |
3 |
4 |
1 |
8 |
64 |
120 |
4 |
16 |
28 |
64 |
||
|
1 |
8 |
15 |
64 |
|
|
|
|
1 |
2 |
3 |
9 |
1 |
9 |
45 |
81 |
4 |
20 |
36 |
100 |
||
|
1 |
8 |
36 |
64 |
|
|
|
|
1 |
2 |
4 |
7 |
1 |
9 |
81 |
153 |
4 |
30 |
56 |
225 |
||
|
1 |
9 |
45 |
81 |
|
|
|
|
1 |
3 |
5 |
9 |
1 |
15 |
120 |
225 |
5 |
9 |
15 |
25 |
||
|
1 |
9 |
81 |
153 |
|
|
|
|
1 |
3 |
5 |
25 |
2 |
3 |
4 |
8 |
5 |
15 |
25 |
45 |
||
|
2 |
4 |
6 |
8 |
|
|
|
|
1 |
3 |
6 |
9 |
2 |
4 |
5 |
8 |
5 |
15 |
30 |
45 |
||
|
2 |
4 |
6 |
9 |
|
|
|
|
1 |
3 |
9 |
15 |
2 |
4 |
6 |
9 |
5 |
25 |
45 |
81 |
||
|
4 |
6 |
8 |
9 |
|
|
|
|
1 |
4 |
7 |
16 |
2 |
4 |
8 |
12 |
6 |
9 |
12 |
16 |
||
|
4 |
6 |
8 |
16 |
|
|
|
|
1 |
4 |
7 |
49 |
2 |
7 |
12 |
72 |
6 |
36 |
66 |
121 |
||
|
9 |
15 |
20 |
25 |
|
|
|
|
1 |
4 |
16 |
28 |
2 |
9 |
12 |
16 |
7 |
16 |
20 |
25 |
||
|
9 |
25 |
45 |
81 |
|
|
|
|
1 |
5 |
9 |
25 |
2 |
12 |
42 |
72 |
7 |
16 |
28 |
49 |
||
|
9 |
81 |
153 |
289 |
|
|
|
|
1 |
5 |
9 |
81 |
3 |
6 |
9 |
12 |
7 |
49 |
91 |
169 |
||
|
|
|
|
|
|
|
|
|
1 |
5 |
15 |
25 |
3 |
9 |
15 |
25 |
8 |
9 |
12 |
16 |
||
|
|
|
|
|
|
|
|
|
1 |
5 |
25 |
45 |
4 |
5 |
6 |
9 |
8 |
64 |
120 |
225 |
||
|
|
|
|
|
|
|
|
|
1 |
5 |
25 |
49 |
4 |
6 |
8 |
9 |
9 |
12 |
15 |
16 |
||
|
|
|
|
|
|
|
|
|
1 |
6 |
36 |
66 |
4 |
6 |
8 |
16 |
9 |
12 |
15 |
25 |
||
|
|
|
|
|
|
|
|
|
1 |
7 |
25 |
49 |
4 |
8 |
12 |
16 |
9 |
12 |
16 |
20 |
||
|
|
|
|
|
|
|
|
|
1 |
7 |
28 |
49 |
4 |
8 |
12 |
36 |
9 |
15 |
20 |
25 |
||
|
|
|
|
|
|
|
|
|
1 |
7 |
49 |
91 |
4 |
8 |
16 |
28 |
9 |
25 |
45 |
81 |
||
|
|
|
|
|
|
|
|
|
1 |
8 |
15 |
64 |
4 |
12 |
20 |
36 |
9 |
45 |
81 |
225 |
||
|
|
|
|
|
|
|
|
|
1 |
8 |
15 |
225 |
4 |
12 |
20 |
100 |
9 |
81 |
153 |
289 |
||
|
|
|
|
|
|
|
|
|
1 |
8 |
36 |
64 |
4 |
16 |
28 |
49 |
|
|
|
|
||
|
12 konbinazio |
konbinazio bat |
65 konbinazio |
|||||||||||||||||||
Goiko taulako 78 konbinazioek aukeren banaketa hau ematen dute, gorago azaldu dugun irizpidea erabiliz:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
154 |
67 |
261 |
158 |
125 |
169 |
109 |
120 |
78 |
128 |
24 |
1 |
103 |
27 |
17 |
2 |
82 |
4 |
21 |
4 |
12 |
|
1.666 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
51 |
116 |
74 |
206 |
158 |
127 |
98 |
103 |
4 |
31 |
69 |
3 |
30 |
14 |
41 |
|
14 |
7 |
8 |
|
20 |
|
1.174 |
Lau balioko konbinazioetan bi progresio egotea zaila zela zirudien arren, taula honek erakusten digu ez dela horrela. Guztira, pieza argiek 1.666 aukera biltzen dituzte bi progresio konbinazio batean osatzeko, eta ilunek 1.174 aukera. Aukera horiek guztiek 710 konbinazio garaile sortzen dituzte 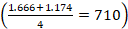 . Pieza argien artean 4 baliodunek aukera gehien sortzen dute, 261; pieza ilunen artean, 9 baliodunek 206 aukera sortzen dituzte. Piramide argiak lau konbinazio osa ditzake, eta ilunak bat ere ez.
. Pieza argien artean 4 baliodunek aukera gehien sortzen dute, 261; pieza ilunen artean, 9 baliodunek 206 aukera sortzen dituzte. Piramide argiak lau konbinazio osa ditzake, eta ilunak bat ere ez.
Progresio aritmetikoak eta harmonikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
|||||||||||||||||||
|
9 |
15 |
45 |
81 |
|
|
|
|
1 |
3 |
5 |
15 |
4 |
5 |
6 |
12 |
9 |
15 |
45 |
81 |
||
|
|
|
|
|
|
|
|
|
1 |
4 |
7 |
28 |
4 |
6 |
12 |
20 |
12 |
15 |
20 |
28 |
||
|
|
|
|
|
|
|
|
|
1 |
5 |
9 |
45 |
4 |
12 |
15 |
20 |
15 |
20 |
25 |
30 |
||
|
|
|
|
|
|
|
|
|
1 |
8 |
15 |
120 |
5 |
7 |
9 |
45 |
15 |
30 |
36 |
45 |
||
|
|
|
|
|
|
|
|
|
3 |
4 |
5 |
6 |
6 |
7 |
8 |
12 |
30 |
36 |
42 |
45 |
||
|
|
|
|
|
|
|
|
|
3 |
4 |
5 |
15 |
9 |
12 |
15 |
45 |
72 |
81 |
90 |
120 |
||
|
|
|
|
|
|
|
|
|
3 |
5 |
7 |
15 |
9 |
15 |
30 |
45 |
|
|
|
|
||
|
konbinazio bat |
konbinaziorik ez |
20 konbinazio |
|||||||||||||||||||
Ikus dezagun konbinazio horiek sortzen dituzten aukerak balioen arabera banatuta:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
7 |
|
26 |
20 |
3 |
13 |
39 |
|
15 |
3 |
4 |
4 |
35 |
|
|
3 |
10 |
|
|
|
|
|
182 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
11 |
24 |
9 |
14 |
22 |
|
2 |
3 |
17 |
4 |
|
|
|
|
5 |
3 |
|
4 |
|
|
|
|
118 |
Bi progresio hauek dituzten konbinazioak sortzea zailagoa da; izan ere, pieza argiek 182 aukera biltzen dituzte eta pieza ilunek 118 baino ez. Aukera horiek guztiek 75 konbinazio garaile sortzen dituzte 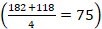 . Oraingoan, balio erabilienak 15a, pieza argien artean, eta 5, pieza ilunen artean, dira. Piramideek ezin dute horrelako konbinaziorik osatu.
. Oraingoan, balio erabilienak 15a, pieza argien artean, eta 5, pieza ilunen artean, dira. Piramideek ezin dute horrelako konbinaziorik osatu.
Progresio geometrikoak eta harmonikoak
|
pieza argien konbinazioak |
pieza ilunen konbinazioak |
konbinazio nahasiak |
|||||||||||||||||||
|
9 |
15 |
25 |
45 |
|
|
|
|
2 |
3 |
6 |
12 |
5 |
9 |
15 |
45 |
9 |
25 |
45 |
225 |
||
|
|
|
|
|
|
|
|
|
3 |
4 |
6 |
12 |
5 |
9 |
45 |
225 |
20 |
30 |
36 |
45 |
||
|
|
|
|
|
|
|
|
|
3 |
5 |
15 |
45 |
9 |
12 |
16 |
72 |
20 |
30 |
45 |
90 |
||
|
|
|
|
|
|
|
|
|
3 |
6 |
8 |
12 |
9 |
15 |
25 |
45 |
25 |
30 |
36 |
45 |
||
|
|
|
|
|
|
|
|
|
4 |
6 |
12 |
36 |
9 |
15 |
45 |
225 |
25 |
45 |
81 |
225 |
||
|
konbinazio bat |
konbinaziorik ez |
15 konbinazio |
|||||||||||||||||||
Progresio geometrikoak eta harmonikoak dituzten hamasei konbinazio horiek aukeren banaketa hau ematen dute:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
2 |
28 |
32 |
2 |
31 |
28 |
7 |
5 |
42 |
21 |
|
89 |
|
|
15 |
10 |
|
|
|
|
|
312 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
11 |
9 |
|
34 |
47 |
8 |
29 |
|
23 |
23 |
|
|
|
|
5 |
1 |
|
|
|
|
42 |
|
232 |
Konbinazio mota hauek aurrekoak baino maizago lortzen dira; izan ere, pieza argiek 312 aukera biltzen dituzte eta pieza ilunek 232 aukera. Aukera horiek guztiek, orain, 136 konbinazio garaile sortzen dituzte 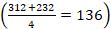 . Aipatzekoa da 45 balioa daramaten pieza argiek honelako konbinazioak osatzeko dituzten aukerak, 89 hain zuzen. Pieza ilunen artean, balio erabiliena 12 da. Piramideek ezin dute horrelako konbinaziorik osatu.
. Aipatzekoa da 45 balioa daramaten pieza argiek honelako konbinazioak osatzeko dituzten aukerak, 89 hain zuzen. Pieza ilunen artean, balio erabiliena 12 da. Piramideek ezin dute horrelako konbinaziorik osatu.
Laburbilduz, piezen zenbakizko balioekin, guztira, 115 konbinazio osa daitezke; konbinazio horiek guztiek garaipen handia ematen dute. Baina, piezen itxura kontuan hartuz gero, konbinazio garailea lortzeko aukerak ugaritzen dira. Hona hemen taula:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
161 |
69 |
315 |
210 |
130 |
213 |
176 |
127 |
98 |
173 |
49 |
5 |
227 |
27 |
17 |
20 |
102 |
4 |
21 |
4 |
12 |
|
2.160 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
73 |
149 |
83 |
254 |
227 |
135 |
129 |
106 |
44 |
58 |
69 |
3 |
30 |
14 |
51 |
4 |
14 |
11 |
8 |
|
62 |
|
1.524 |
Garaipen handia lortzeko pieza argiek aukera gehiago dute ilunek baino, 2.160 aukera eta 1.524 aukera, hurrenez hurren. Guztira, orduan, garaipen handia lortzeko, 921 konbinazio garaile daude 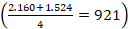 . Gehien erabiltzen diren piezak dira 4 baliodunak, pieza argien artean, eta 9 baliodunak, pieza ilunen artean dira.
. Gehien erabiltzen diren piezak dira 4 baliodunak, pieza argien artean, eta 9 baliodunak, pieza ilunen artean dira.
Garaipen bikainak
Boissièrek eta Barozzik piezen balioen artean ematen diren proportzioak aipatzen dituzte: sesquialtera, sesquiterza, dupla, tripla eta quadrupla eta horiei dagozkien kontsonantzia musikalak diapente (bostuna), diatessaron (lauduna), diapasson (zortziduna), diapasson eta diapente (hamabiduna) elkarrekin, disdiapasson (hamabostuna) eta tonu osoa. Ematen dituzten konbinazioen adibideetan, bost harmonia horiek ematen dira konbinazioko balioen eta balioen arteko kenduren artean. Hortik datozkio garaipen mota honi erabiltzen dituzten kalifikatzaile guztiak: præstantissima, admirabile, incredibilem (Boissière), massima, eccellentissima, ultima vitoria (Barozzi). Boissièrek eta Barozzik aipatzen dituzten bost harmonia horiek dituzten konbinazioak 2.288 dira. Konbinazio gehiegitxo irabazteko eta garaipen bikainena izateko, eman zituzten zerrendekin erkatuz gero.
Kasu honetan, hiru progresioak dituzten konbinazioak osatu behar dituzte jokalariek lau piezekin: aritmetikoa, geometrikoa eta harmonikoa, aldi berean. Egileek hainbat taula ematen dituzte garaipen bikaina lortzeko konbinazioekin. Taulen egileek, ordea, ez dute zehazten nola lortu dituzten konbinazioak, ezta horiek konbinazio bakarrak diren. Hona lau egileek eman zituzten taulak ekarri ditugu. Boissièrek (1556) zortzi konbinazio eman zituen; konbinazio batek zenbaki oker bat du (laranja kolorekoa). Barozzik (1572) konbinazio bat gehiago (laranja argikoa) eman zuen bere taulan, eta balio okerra errepikatu zuen (laranja iluna). Fulkek (1563) taula luzeagoa eman zuen konbinazio gehiagorekin (berde argiko konbinazioak), hogeita bederatzi konbinazio emanez eta aurrekoen akatsa zuzenduz; hala ere, berak ere balio oker pare bat eman zuen (laranja iluna). Mebbenek (1996) Fulkeren taula zuzendu du, konbinazio bat kenduz (lauki grisekoak) eta bi okerrak zuzenduz (urdin argikoak).
| Claude de Boissière | Francesco Barozzi | William Fulke eta Ralph Lever | Peter Mebben | |||||||||||||||
|
2 |
3 |
4 |
6 |
2 |
3 |
4 |
6 |
2 |
3 |
4 |
6 |
2 |
3 |
4 |
6 |
|||
|
3 |
5 |
15 |
25 |
2 |
9 |
16 |
72 |
2 |
3 |
6 |
9 |
2 |
3 |
6 |
9 |
|||
|
4 |
6 |
8 |
12 |
3 |
5 |
15 |
25 |
2 |
4 |
6 |
12 |
2 |
4 |
6 |
12 |
|||
|
4 |
6 |
9 |
12 |
4 |
6 |
8 |
12 |
2 |
5 |
8 |
20 |
2 |
5 |
8 |
20 |
|||
|
5 |
9 |
45 |
91 |
4 |
6 |
9 |
12 |
2 |
7 |
12 |
42 |
2 |
7 |
12 |
42 |
|||
|
5 |
25 |
45 |
225 |
5 |
9 |
45 |
91 |
2 |
9 |
16 |
72 |
2 |
9 |
16 |
72 |
|||
|
6 |
8 |
9 |
12 |
5 |
25 |
45 |
225 |
3 |
4 |
6 |
8 |
3 |
4 |
6 |
8 |
|||
|
12 |
15 |
16 |
20 |
6 |
8 |
9 |
12 |
3 |
4 |
6 |
9 |
3 |
4 |
6 |
9 |
|||
|
12 |
15 |
16 |
20 |
3 |
5 |
9 |
15 |
3 |
5 |
9 |
15 |
|||||||
|
3 |
5 |
15 |
25 |
3 |
5 |
15 |
25 |
|||||||||||
|
3 |
9 |
15 |
45 |
3 |
9 |
15 |
45 |
|||||||||||
|
4 |
6 |
8 |
12 |
4 |
6 |
8 |
12 |
|||||||||||
|
4 |
6 |
9 |
12 |
4 |
6 |
9 |
12 |
|||||||||||
|
4 |
7 |
16 |
28 |
4 |
7 |
16 |
28 |
|||||||||||
|
4 |
7 |
28 |
49 |
4 |
7 |
28 |
49 |
|||||||||||
|
5 |
6 |
25 |
45 |
5 |
9 |
25 |
45 |
|||||||||||
|
5 |
9 |
45 |
81 |
5 |
9 |
45 |
81 |
|||||||||||
|
5 |
15 |
25 |
45 |
5 |
25 |
45 |
225 |
|||||||||||
|
5 |
25 |
45 |
225 |
6 |
8 |
9 |
12 |
|||||||||||
|
6 |
8 |
9 |
12 |
6 |
8 |
12 |
16 |
|||||||||||
|
6 |
8 |
12 |
16 |
7 |
12 |
42 |
72 |
|||||||||||
|
6 |
12 |
15 |
20 |
8 |
15 |
64 |
120 |
|||||||||||
|
7 |
12 |
42 |
72 |
8 |
15 |
120 |
225 |
|||||||||||
|
8 |
15 |
64 |
120 |
9 |
12 |
15 |
20 |
|||||||||||
|
8 |
15 |
120 |
225 |
12 |
15 |
16 |
20 |
|||||||||||
|
12 |
15 |
16 |
20 |
12 |
15 |
20 |
25 |
|||||||||||
|
12 |
15 |
20 |
25 |
15 |
20 |
30 |
45 |
|||||||||||
|
15 |
20 |
30 |
45 |
15 |
30 |
45 |
90 |
|||||||||||
|
15 |
30 |
45 |
90 |
|||||||||||||||
| 8 konbinazio | 9 konbinazio | 29 konbinazio | 28 konbinazio | |||||||||||||||
Hala ere, konbinazio horietatik guztietatik hiru konbinaziok baino ez dute betetzen hiru progresioak dituztela (granate kolorekoak aurreko tauletan):
|
Progresio aritmetiko, geometriko eta harmonikoak |
p. aritmetikoa |
p. geometrikoa |
p. harmonikoa |
||||||||||||
|
3 |
4 |
6 |
9 |
3 |
6 |
9 |
4 |
6 |
9 |
3 |
4 |
6 |
|||
|
4 |
6 |
9 |
12 |
6 |
9 |
12 |
4 |
6 |
9 |
4 |
6 |
12 |
|||
|
15 |
20 |
30 |
45 |
15 |
30 |
45 |
20 |
30 |
45 |
15 |
20 |
30 |
|||
|
3 progresio aritmetiko, geometriko eta harmoniko |
|||||||||||||||
Gainerako konbinazioek, ordea, progresio aritmetikoa eta progresio harmonikoa dute, baina ez progresio geometrikoa. Progresio geometrikoaren ordez, beste erlazio hau betetzen dute, A, B, C eta D badira 4 piezen balioak:
| A | B | C | D |
propietate hau betetzen dute: 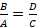 edo
edo 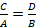 edo
edo 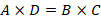 .
.
Badirudi Erdi Aroan propietate hori erabili zela horrelako konbinazio bat progresio geometriko gisa onartzeko. Orduan, propietate horrek progresio geometrikoarena ordeztu zuen garaipen bikaina lortzeko konbinazioak osatzerakoan.
Bi aukera horiek, hiru progresioak izatea edo progresio aritmetikoa, progresio harmonikoa eta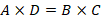 propietatea betetzea, kontuan hartzen baditugu eta betetzen dituzten konbinazioak garailetzat ematen baditugu, 28 konbinazio izango ditugu garaipen bikaina lortzeko.
propietatea betetzea, kontuan hartzen baditugu eta betetzen dituzten konbinazioak garailetzat ematen baditugu, 28 konbinazio izango ditugu garaipen bikaina lortzeko.
|
hiru progresioak |
progresio aritmetikoa, progresio harmonikoa eta |
||||||||||||||||||||
|
pieza argien konbinazioak |
konbinazio nahasiak |
||||||||||||||||||||
|
3 |
4 |
6 |
9 |
2 |
9 |
16 |
72 |
2 |
3 |
4 |
6 |
3 |
9 |
15 |
45 |
7 |
12 |
42 |
72 |
||
|
4 |
6 |
9 |
12 |
|
|
|
|
2 |
3 |
6 |
9 |
4 |
6 |
8 |
12 |
8 |
15 |
64 |
120 |
||
|
15 |
20 |
30 |
45 |
|
|
|
|
2 |
4 |
6 |
12 |
4 |
7 |
16 |
28 |
8 |
15 |
120 |
225 |
||
|
|
|
|
|
|
|
|
|
2 |
5 |
8 |
20 |
4 |
7 |
28 |
49 |
9 |
12 |
15 |
20 |
||
|
|
|
|
|
|
|
|
|
2 |
7 |
12 |
42 |
5 |
9 |
25 |
45 |
12 |
15 |
16 |
20 |
||
|
|
|
|
|
|
|
|
|
2 |
9 |
16 |
72 |
5 |
9 |
45 |
81 |
12 |
15 |
20 |
25 |
||
|
|
|
|
|
|
|
|
|
3 |
4 |
6 |
8 |
5 |
25 |
45 |
225 |
15 |
30 |
45 |
90 |
||
|
|
|
|
|
|
|
|
|
3 |
5 |
9 |
15 |
6 |
8 |
9 |
12 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3 |
5 |
15 |
25 |
6 |
8 |
12 |
16 |
|
|
|
|
||
|
3 konbinazio |
konbinazio bat |
25 konbinazio |
|||||||||||||||||||
Hiru progresioak dituzten hiru konbinazioetan bi jokalarien piezak behar dira. Pieza argiek abantaila dute, hamabi piezetatik zazpi argiak direlako, hiru ilunak dira eta bi pieza bionak dira. Konbinazio horiek aukera hauek ematen dituzte:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
|
44 |
44 |
|
20 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
111 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
22 |
|
|
24 |
22 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |
Guztira, 45 konbinazio garaile desberdin daude 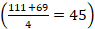 .
.
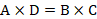 propietatea betetzen dituzten 26 konbinazioetatik bat pieza argiekin egin daiteke; gainerakoak osatzeko bi jokalarien piezak behar dira. Konbinazioak osatzeko aukeren banaketa hau da:
propietatea betetzen dituzten 26 konbinazioetatik bat pieza argiekin egin daiteke; gainerakoak osatzeko bi jokalarien piezak behar dira. Konbinazioak osatzeko aukeren banaketa hau da:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
33 |
83 |
84 |
29 |
56 |
32 |
18 |
15 |
20 |
|
2 |
42 |
3 |
1 |
16 |
8 |
|
|
|
|
|
442 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
47 |
46 |
25 |
62 |
65 |
20 |
14 |
23 |
2 |
|
9 |
|
2 |
|
4 |
1 |
|
4 |
|
|
6 |
|
330 |
Pieza argiek 442 aukera dituzte, eta pieza ilunek 330 aukera. Guztira, beraz, 193 konbinazio garaile daude 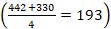 .
.
Laburbilduz, piezen zenbakizko balioekin, guztira, 28 konbinazio osa daitezke; konbinazio horiek guztiek garaipen bikaina ematen dute. Baina, piezen itxura kontuan hartuz gero, konbinazio garailea lortzeko aukerak ugaritzen dira. Hona hemen taula:
|
piezak |
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
|
aukerak |
|
33 |
127 |
128 |
29 |
76 |
33 |
18 |
16 |
20 |
|
2 |
43 |
3 |
1 |
16 |
8 |
|
|
|
|
|
553 |
|
piezak |
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
aukerak |
69 |
46 |
25 |
86 |
87 |
20 |
14 |
23 |
3 |
|
9 |
|
2 |
|
4 |
1 |
|
4 |
|
|
6 |
|
399 |
Garaipen bikaina lortzeko pieza argiek aukera gehiago dute ilunek baino, 553 aukera eta 399 aukera, hurrenez hurren. Guztira, orduan, garaipen bikaina lortzeko, 238 konbinazio garaile desberdin daude 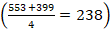 . Gehien erabiltzen diren piezak, argien artean 6 eta 4 baliodunak eta, ilunen artean, 12 eta 9 baliodunak dira.
. Gehien erabiltzen diren piezak, argien artean 6 eta 4 baliodunak eta, ilunen artean, 12 eta 9 baliodunak dira.
Hiru garaipen motak, hala moduzkoa, handia eta bikaina, biltzen baditugu, guztira, 1.634 konbinazio garaile daude 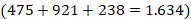 .
.
Datu hauek esaten digute piezen balioek zenbat konbinazio garaile osatzen duten garaipena lortzeko:
|
|
|
1 |
2 |
4 |
6 |
8 |
9 |
15 |
16 |
20 |
25 |
36 |
42 |
45 |
49 |
64 |
72 |
81 |
91* |
153 |
169 |
289 |
|
|
Hala moduzko garaipenak |
PA |
23 |
32 |
51 |
46 |
33 |
30 |
20 |
18 |
26 |
23 |
15 |
21 |
10 |
8 |
5 |
7 |
16 |
5 |
7 |
1 |
2 |
399 |
|
PG |
37 |
6 |
48 |
18 |
11 |
20 |
7 |
38 |
9 |
18 |
30 |
2 |
12 |
4 |
8 |
3 |
44 |
1 |
2 |
1 |
2 |
321 |
|
|
PH |
|
2 |
15 |
16 |
4 |
11 |
8 |
7 |
3 |
3 |
2 |
1 |
18 |
|
|
16 |
|
|
|
|
|
106 |
|
|
Garaipen handiak |
PAG |
154 |
67 |
261 |
158 |
125 |
169 |
109 |
120 |
78 |
128 |
24 |
1 |
103 |
27 |
17 |
2 |
82 |
4 |
21 |
4 |
12 |
1.666 |
|
PAH |
7 |
|
26 |
20 |
3 |
13 |
39 |
|
15 |
3 |
4 |
4 |
35 |
|
|
3 |
10 |
|
|
|
|
182 |
|
|
PGH |
|
2 |
28 |
32 |
2 |
31 |
28 |
7 |
5 |
42 |
21 |
|
89 |
|
|
15 |
10 |
|
|
|
|
312 |
|
|
Garaipen bikainak |
PAGH |
|
|
44 |
44 |
|
20 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
111 |
|
A×D=B×C |
|
33 |
83 |
84 |
29 |
56 |
32 |
18 |
15 |
20 |
|
2 |
42 |
3 |
1 |
16 |
8 |
|
|
|
|
442 |
|
|
|
|
221 |
142 |
556 |
418 |
207 |
350 |
244 |
208 |
152 |
237 |
96 |
31 |
310 |
42 |
31 |
62 |
170 |
10 |
30 |
6 |
16 |
3.539 |
|
|
|
3 |
5 |
7 |
9 |
12 |
16 |
25 |
28 |
30 |
36 |
49 |
56 |
64 |
66 |
81 |
90 |
100 |
120 |
121 |
190* |
225 |
361 |
|
|
Hala moduzko garaipenak |
PA |
24 |
29 |
26 |
26 |
31 |
26 |
16 |
23 |
17 |
11 |
23 |
15 |
8 |
10 |
4 |
8 |
3 |
8 |
2 |
1 |
4 |
|
315 |
|
PG |
4 |
5 |
4 |
16 |
18 |
34 |
5 |
5 |
9 |
38 |
13 |
5 |
9 |
2 |
18 |
3 |
7 |
2 |
2 |
1 |
12 |
1 |
213 |
|
|
PH |
9 |
6 |
4 |
12 |
10 |
8 |
2 |
3 |
6 |
2 |
|
|
|
|
|
2 |
|
2 |
|
|
5 |
|
71 |
|
|
Garaipen handiak |
PAG |
51 |
116 |
74 |
206 |
158 |
127 |
98 |
103 |
4 |
31 |
69 |
3 |
30 |
14 |
41 |
|
14 |
7 |
8 |
|
20 |
|
1.174 |
|
PAH |
11 |
24 |
9 |
14 |
22 |
|
2 |
3 |
17 |
4 |
|
|
|
|
5 |
3 |
|
4 |
|
|
|
|
118 |
|
|
PGH |
11 |
9 |
|
34 |
47 |
8 |
29 |
|
23 |
23 |
|
|
|
|
5 |
1 |
|
|
|
|
42 |
|
232 |
|
|
Garaipen bikainak |
PAGH |
22 |
|
|
24 |
22 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |
|
A×D=B×C |
47 |
46 |
25 |
62 |
65 |
20 |
14 |
23 |
2 |
|
9 |
|
2 |
|
4 |
1 |
|
4 |
|
|
6 |
|
330 |
|
|
|
|
179 |
235 |
142 |
394 |
373 |
223 |
166 |
160 |
79 |
109 |
114 |
23 |
49 |
26 |
77 |
18 |
24 |
27 |
12 |
2 |
89 |
1 |
2.522 |
Pieza argien taulan, 4ko eta 6ko piezen garrantzia nabarmentzen da, lehena 556 konbinazio garailetan erabil daiteke, eta bigarrena 418 konbinazio garailetan. Pieza ilunen taulan, ordea, 9ko eta 12ko pieza ilunak dira erabilienak konbinazio garaileak osatzeko, 394 eta 373 konbinazio garailetan, hurrenez hurren.
Bi taulak erkatuz ondo ikusten da pieza argiek aukera gehiago dutela konbinazio garaileak osatzeko ilunek baino, guztira 1.017 aukera gehiago.
Hortaz, erasorako ahalmena neurtzen duten taulak eta garaipena lortzeko aukerak ematen dituzten taulak kontuan hartuz, ondoriozta daiteke argiek abantaila nabarmena dutela ritmomakia jokoan, bai aurkariaren piezak erasotzeko bai garaipena ematen duten harmoniak osatzeko.
Iturriak
Francesco Barozzi: Il nobilissimo et antiquissimo giuoco pythagoreo nominato Rythmomachia. Venezia, 1572. (https://archive.org/details/bub_gb_PQZovyIc70gC/page/n23/mode/2up, 2020-12-31)
Claude de Boissière: Nobilissimus et antiquissimus ludus pythagoreus (qui Rhythmomachia nominatur). Paris, 1556. (https://babel.hathitrust.org/cgi/pt?id=ucm.5317951422&view=1up&seq=7, 2020-12-31)
Arno Borst: Das mittelalterliche Zahlenkampfspiel, Heidelberg, 1986.
Jack Botermans: The Book of Games. Sterling, New York, 2008.
Jean-Louis Cazaux eta Rick Knowlton: A World of Chess. Jefferson, 2017.
William Fulke eta Rafe Lever: The most noble ancient, and learned playe, called the Philosophers Game, Londres, 1563.
Peter Mebben: Rithmomachia, the Philosophers' Game A Mediaeval Battle of Numbers. (http://www.metapontum.nl/en/rub4phil/atta/pdfs/RithmomachiaEN_NL2009.pdf, 2020-12-31)
José M. Núñez: La aritmética de Boecio y la ritmomaquia: Teoría y práctica del juego medieval de los sabios. (http://www.tuttoenumero.it/wp-content/uploads/2013/12/N%C3%9A%C3%91EZ-ESPALLARGAS-LA-ARITM%C3%89TICA-DE-BOECIO-Y-LA-RITMOMAQUIA.pdf, 2020-12-31)
Theoni Pappas: Math for Kids & Other People Too!, Wide World Publishing/Tetra, 1997.
David Eugene Smith eta Clara C. Eaton: Rithmomachia, the Great Medieval Number Game. The American Mathematical Monthly, Vol. 18, No. 4, 1911. (https://www.jstor.org/stable/2973449?seq=4#metadata_info_tab_contents, 2020-12-31)
Jurgen Stitger: Rithmomachia, the Philosophers’ Game. An introduction to its History and Rules (Ancient Board Games in perspective). British Museum, Londres, 2008.
El Mundo de los Juegos. Altaya, Bartzelona, 1999.
Eskuko arauak: Buxaina.
