set
Set karta-jokoa Marsha J. Falco populazioaren genetistak asmatu zuen 1974an. Diseinatzaileak bere lanean genetista gisa erabili zuen kodetze-sistema batetik abiatuta garatu zuen jokoa. Irudiak ISO 5807 arauan oinarritzen dira.
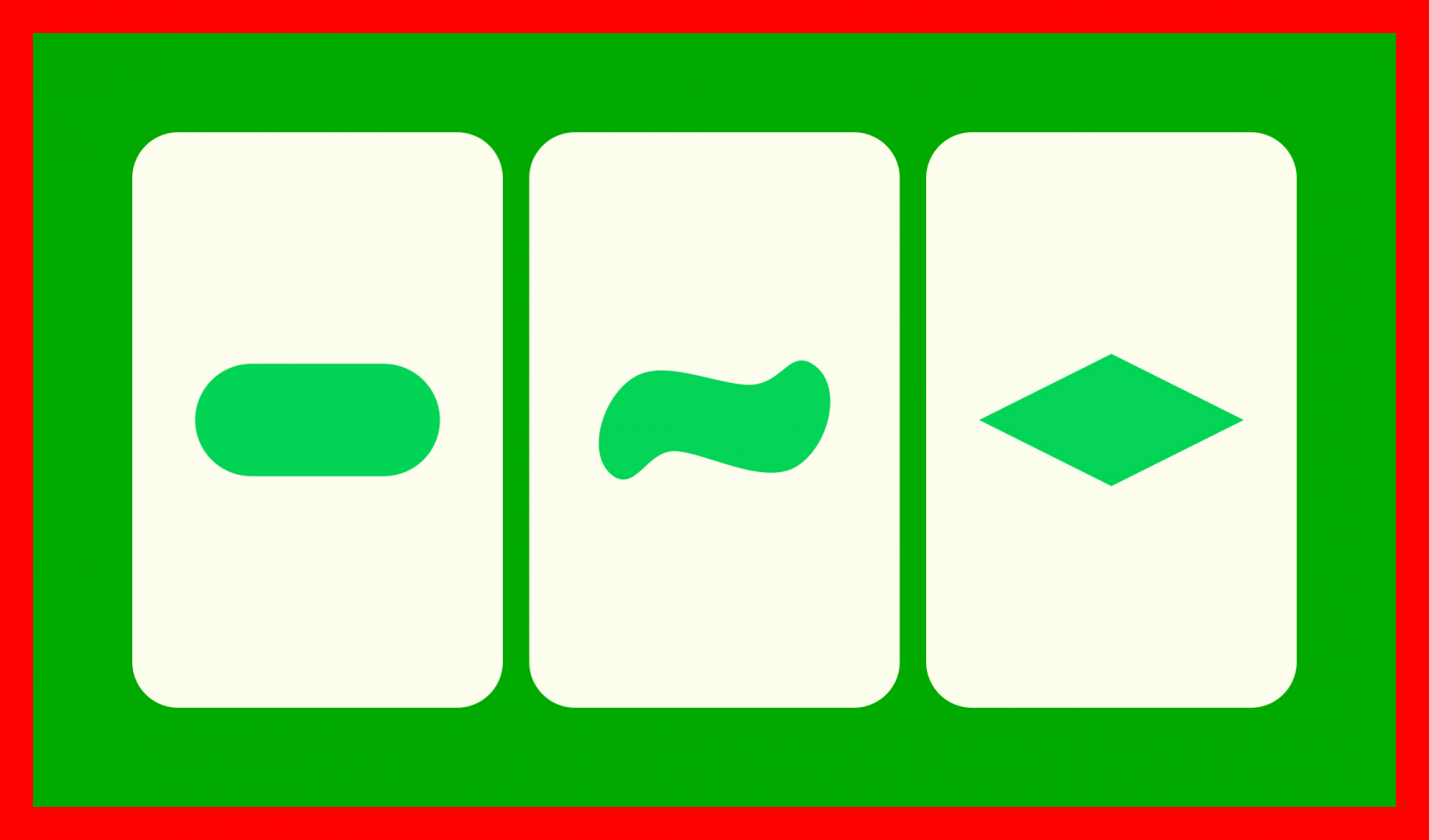
Jokoak 81 karta desberdin ditu launa ezaugarrirekin. Jokoaren helburua SET bat osatzea da. SET bat karten hirukote bat da, non ezaugarri bakoitza hiru kartetan berdina den edo hiru kartetan desberdina den.
1990ean Estatu Batuetan argitaratu ondoren, asko zabaldu zen haurren, ikasleen eta matematikarien artean. Jokatzeko dibertigarria izateaz gain matematika-problema batzuekin lotzen da jokoa.
2003an, Benjamin Lent Davis eta Diane Maclagan-ek The card game SET. The Mathematical Intelligencer 25. 3 idatzi zuten.
2009an Jim Vinci-k set karta-sortari buruzko ikerketak argitaratu zituen artikulu honetan: The Maximum Number of sets for N cards and the Total Number of Internal Sets for all Partitions of the Deck (Multzo kopuru handiena N kartekin eta karta-sortaren edozein partiketarako barneko multzoen kopuru osoa).
2014an, Paola Y. Reyes-ek The Mathematics of the Card Game Set lana idatzi zuen, Honors Projects Overview. Paper 93, Rhode Island College. (http://digitalcommons.ric.edu/honors_projects/93).
2016an Liz McMahon, Gary Gordon, Hannah Gordon eta Rebecca Gordon-ek argitaratu zuten The Joy of Set: The Many Mathematical Dimensions of a Seemingly Simple Card Game (Itxuraz sinplea den karta-joko baten dimentsio matematiko ugariak) liburua jokoaren deskribapen zehatza da.
Besteak beste, matematikariek galdetzen dute gehienez zenbat karta atera daitezkeen hirukoterik gabe, edo, bestela esanda, zein den hirukoteren bat bermatzen duen karta kopuru txikiena. Bitxiki, erantzuna jokoa asmatu baino hiru urte lehenago emana zuen Giuseppe Pellegrino-k Sul massimo ordine delle calotte in S4,3 artikuluan, Matematiche, Catania, 1971. Hirukoterik sortu gabe erakuts daitekeen karta kopuru handiena 20 da.
Set jokoaren orokortze natural bat erabiliz, non ezaugarrien eta balioen kopurua aldatu egiten baita, frogatu zen, banatutako karta-bilduma batetik abiatuta, SET bat dagoen zehaztea NP-osoa dela. Horrela frogatu zuten Kamalika Chaudhuri, Brighten Godfrey, David Ratajczak eta Hoeteck We-k 2003ko On the Complexity of the Game of Set artikuluan.
SET jokoak 25 sari jaso ditu, besteak beste: American Mensa-ren Mensa Select saria irabazi zuen 1991n eta 9.a izan zen 1995eko Deutscher Spiele Preis sarian. Horiez gain, Dr. Toy’s 10 Best saria, Creative Child’s Preferred Choice saria eta Games Magazine-ren Games 100 saria.
Ondoko webgunean set jokoaren aldaera batzuk ikus ditzakezu: http://magliery.com/Set/SetVariants.html
Osagaiak eta hasiera
Set karta-jokoa 81 kartako karta-sorta da.
Karta bakoitzak lau ezaugarri ditu eta ezaugarri bakoitzak hiru aukera:
- Irudia: erronboa, obaloa edo tileta izan daiteke.
- Kopurua: karta bakoitzak irudi bat, bi edo hiru irudi berdin ditu.
- Kolorea: irudia berdea, gorria edo morea izan daiteke.
- Betegarria: irudia betea, hutsik edo marraduna izan daiteke.
Ezaugarrien konbinazio bakoitzerako karta bat dago: 3×3×3×3 = 81.
Partidaren hasieran, hamabi karta jartzen dira ahoz gora.
Jokoaren helburua SET bat azkar aurkitzea da. SET bat karten hirukote bat da, non ezaugarri bakoitza hiru kartetan berdina den edo hiru kartetan desberdina den.

irudi desberdinak, kopuru berdina,
kolore desberdinak, irudi beteak.
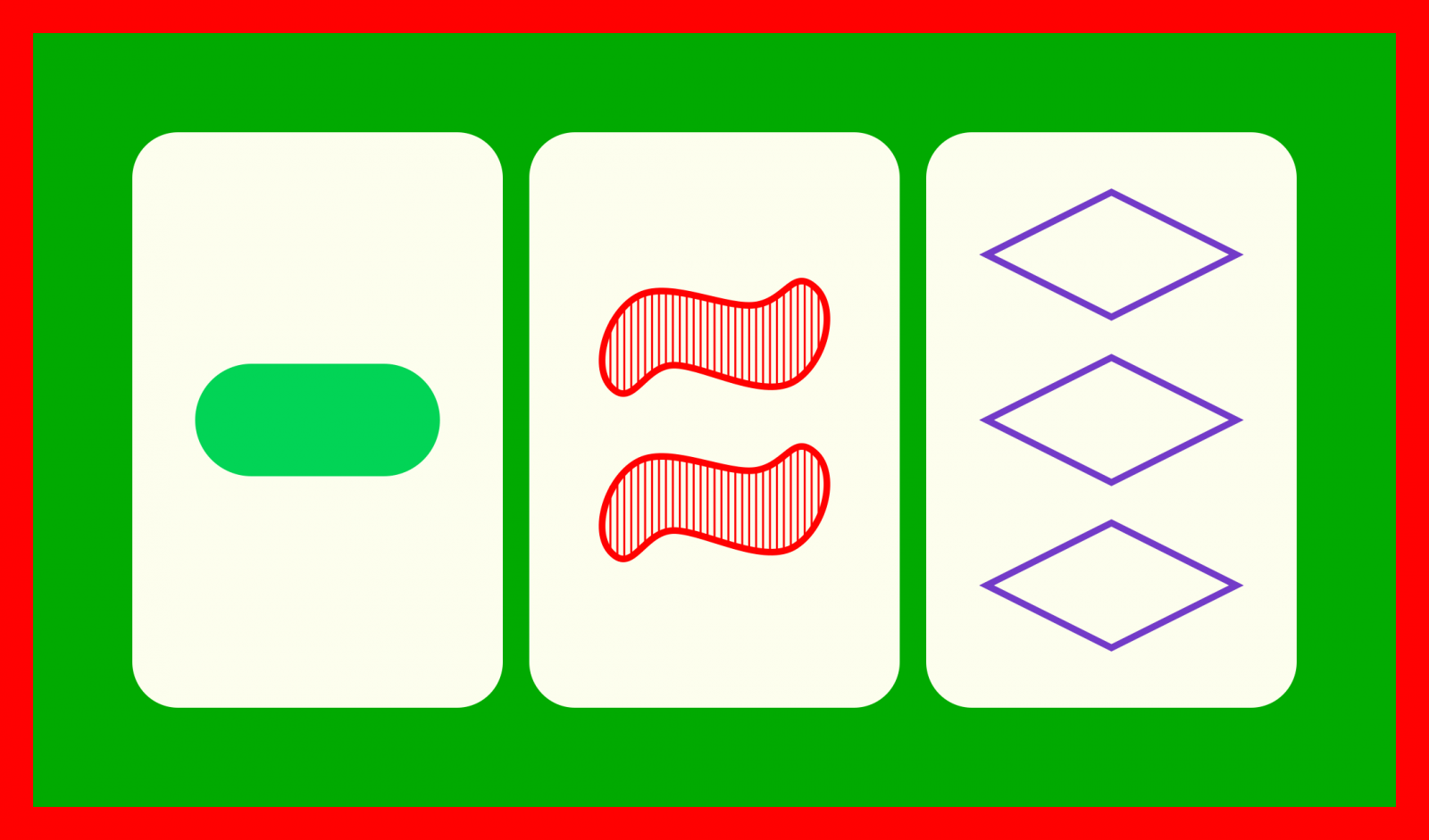
irudi desberdinak, kopuru desberdinak,
kolore desberdinak, betegarri desberdinak.
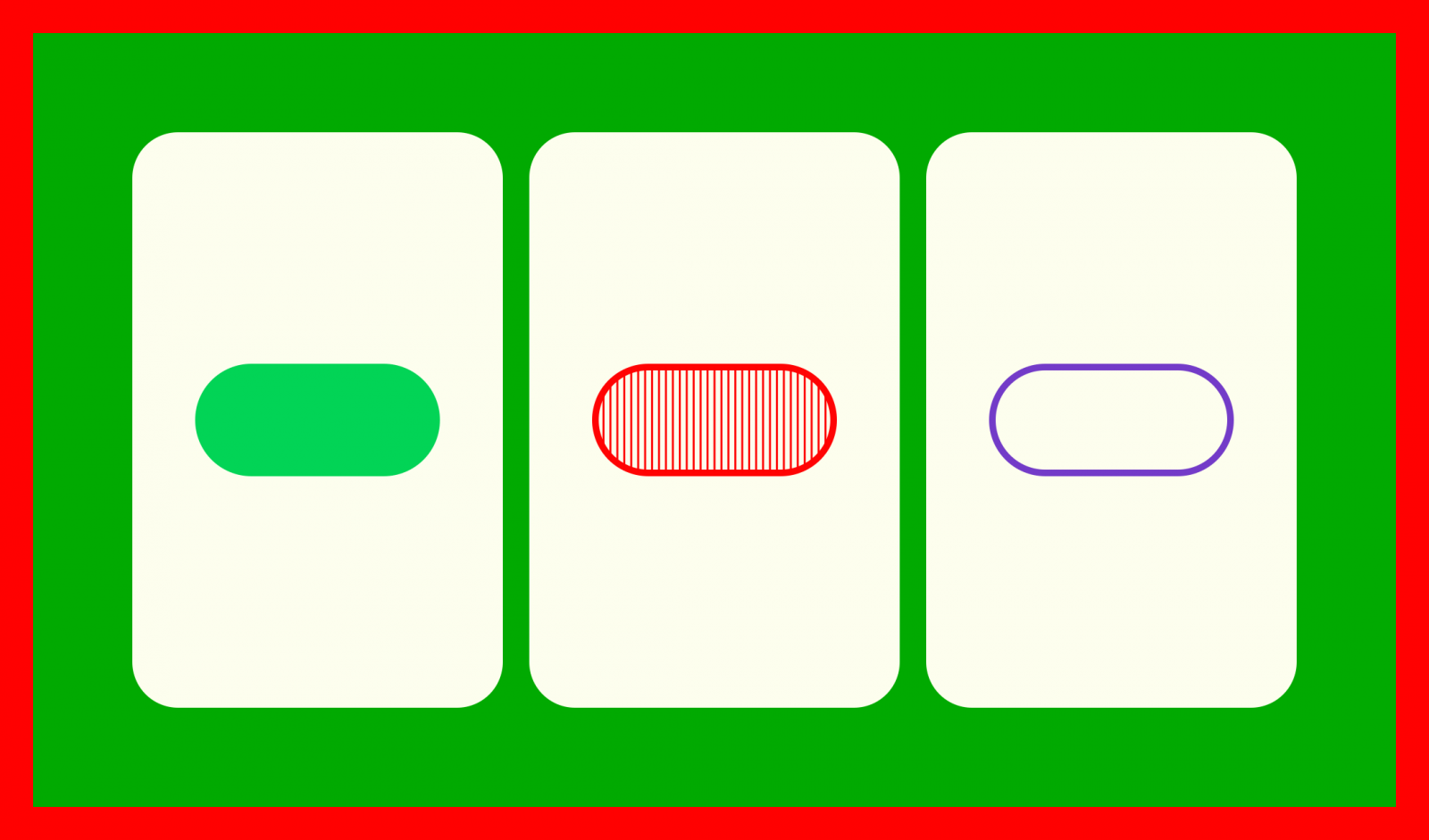
irudi berdinak, kopuru berdinak,
kolore desberdinak, betegarri desberdinak.
Arauak
Karta-sorta nahasi eta gero, hamabi karta ahoz gora jarri behar dira mahaian, 3×4 taula osatuz.
Ez dago txandarik.
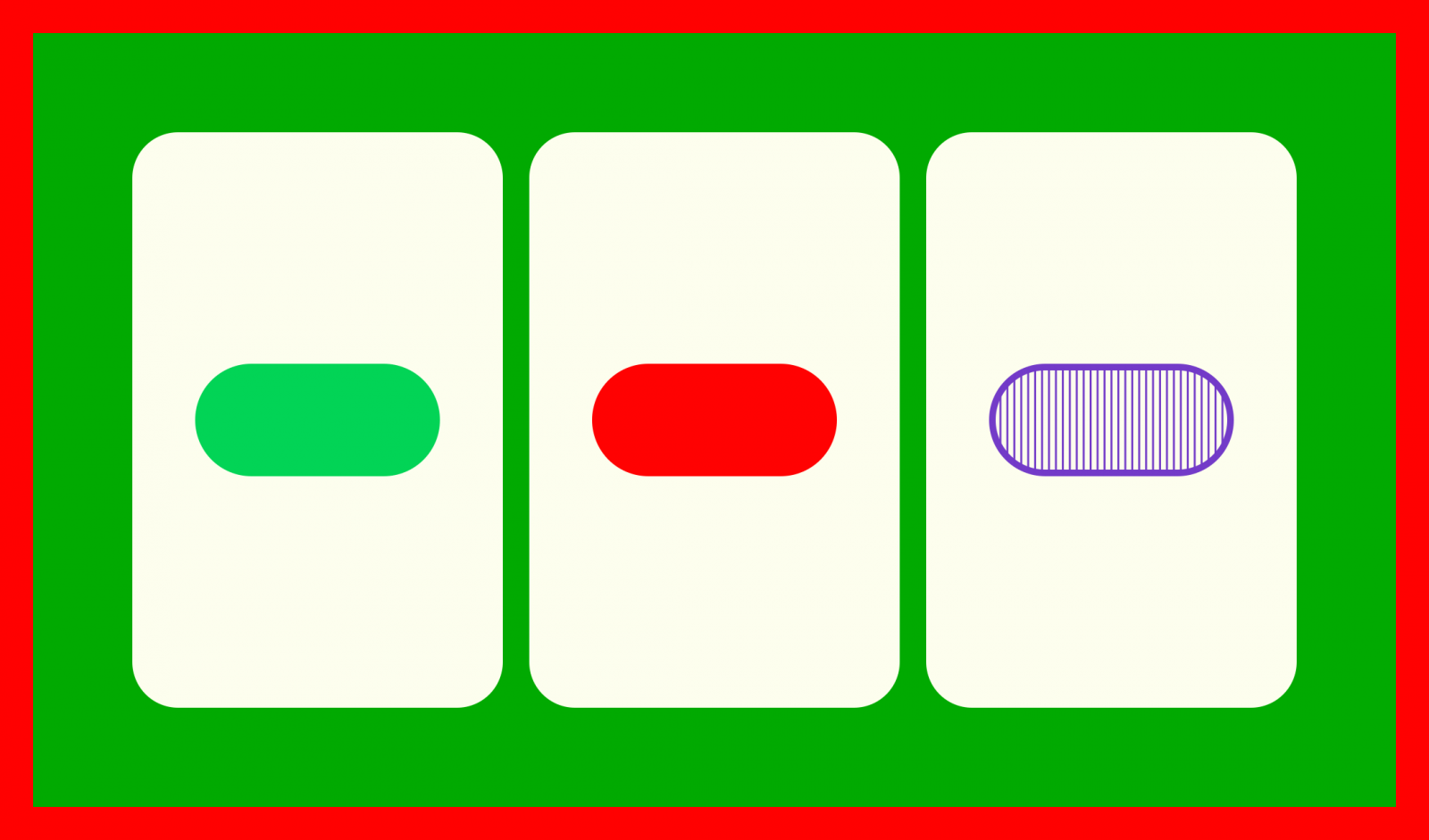
bi kartek irudi betea dute, eta karta batek ez.
Jokalari batek SET bat ikusten badu, “NI” edo “SET” oihukatuko du eta jokoa etengo da, SET hori beste jokalariek egiaztatu arte.
SETa egiaztatzen bada, jokalariak hiru kartak hartuko ditu. Hutsik gertatzen diren posizioak karta berriekin betetzen dira.
SETa ez bada egiaztatzen, jokalariak bere pilatik hiru karta galduko ditu.
Hiru kartek SET bat ez dutela osatzen egiaztatzeko bide azkar bat hau da: ezaugarri bat bi kartetan berdina bada eta hirugarren kartan desberdina bada, ez da SET bat.
Gerta daiteke mahai gainean dauden karten artean SETik ez egotea (edo ez ikustea). Kasu horretan, hiru karta gehigarri jartzen dira mahaian, mahai gainean hamabost karta utziz. Hurrengo SETa osatzen denean, ez dira hiru karta berri aterako, eta berriro hamabi karta geratuko dira mahaian.
Karta guztiak erabiltzen direnean eta mahaiko kartak erabiliz SET gehiagorik ezin denean osatu amaitzen da jokoa.
SET gehien bildu dituen jokalariak irabazi egiten du.
Kartekin trebatzeko honelako ariketak egin daitezke:
- Bi karta emanik, aurkitu SET bat osatzeko erabil daitezkeen kartak.
- Saiatu zazpi SETak aurkitzen ondoko hamabi karten artean:

- Hamabi karta horiekin, zenbat SET osa daitezke karta gehien biltzeko?
- Saiatu 9 karta hauekin 12 kartako multzo bat osatzen SETik gabe:

- Karratu magiko bat 3×3 kartako multzo bat da, non errenkada, zutabe eta diagonal guztiek SET bat osatzen duten. x, y eta z SET bat osatzen ez duten hiru karta badira, erakutsi beti bete dezakegula (modu bakarrean) karratu magiko hau:
| x | y | ? |
| z | ? | ? |
| ? | ? | ? |
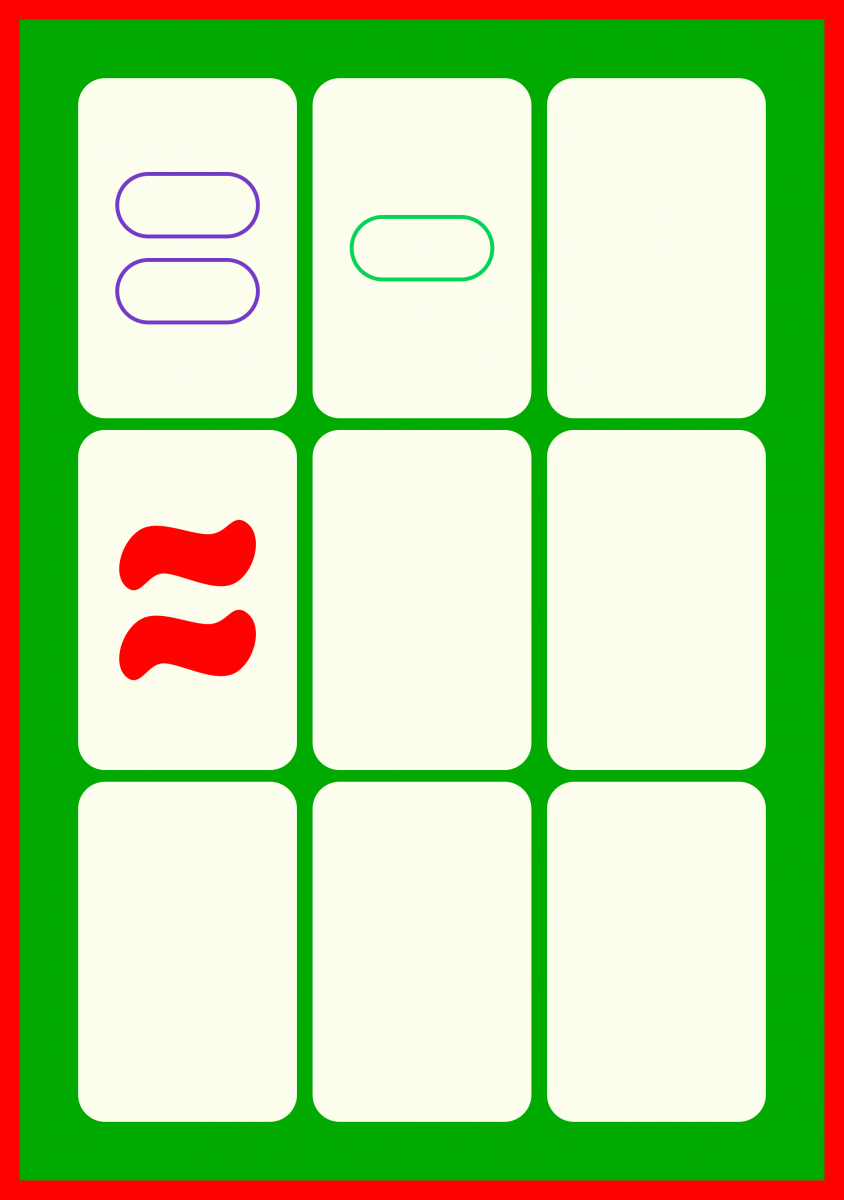
Bestelakoak
Esan bezala SET bat hiru karten hirukote bat da, non ezaugarri bakoitza hiru kartetan berdina den edo hiru kartetan desberdina den. Horrelako hirukote bat osatzeko, lehenago bi karta hartu behar dira. Hirugarren karta bikote horrek zehazten du unibokoki; izan ere, ezaugarri bakoitzaren bi datu ditugu lehenengo bi kartetan eta hirugarren kartak ezaugarri bakoitza osatzeko, ezaugarriarekin bat etorri edo zeharo desberdina izan behar du, hots, ezaugarri bakoitzeko aukera bakarra du eta, beraz, lau ezaugarri horiek dituen karta bakarra dago. Hortaz, esan dezakegu 81 kartekin egin daitezkeen SETen kopurua bikote kopurua dela: ![]() SET desberdin daude.
SET desberdin daude.
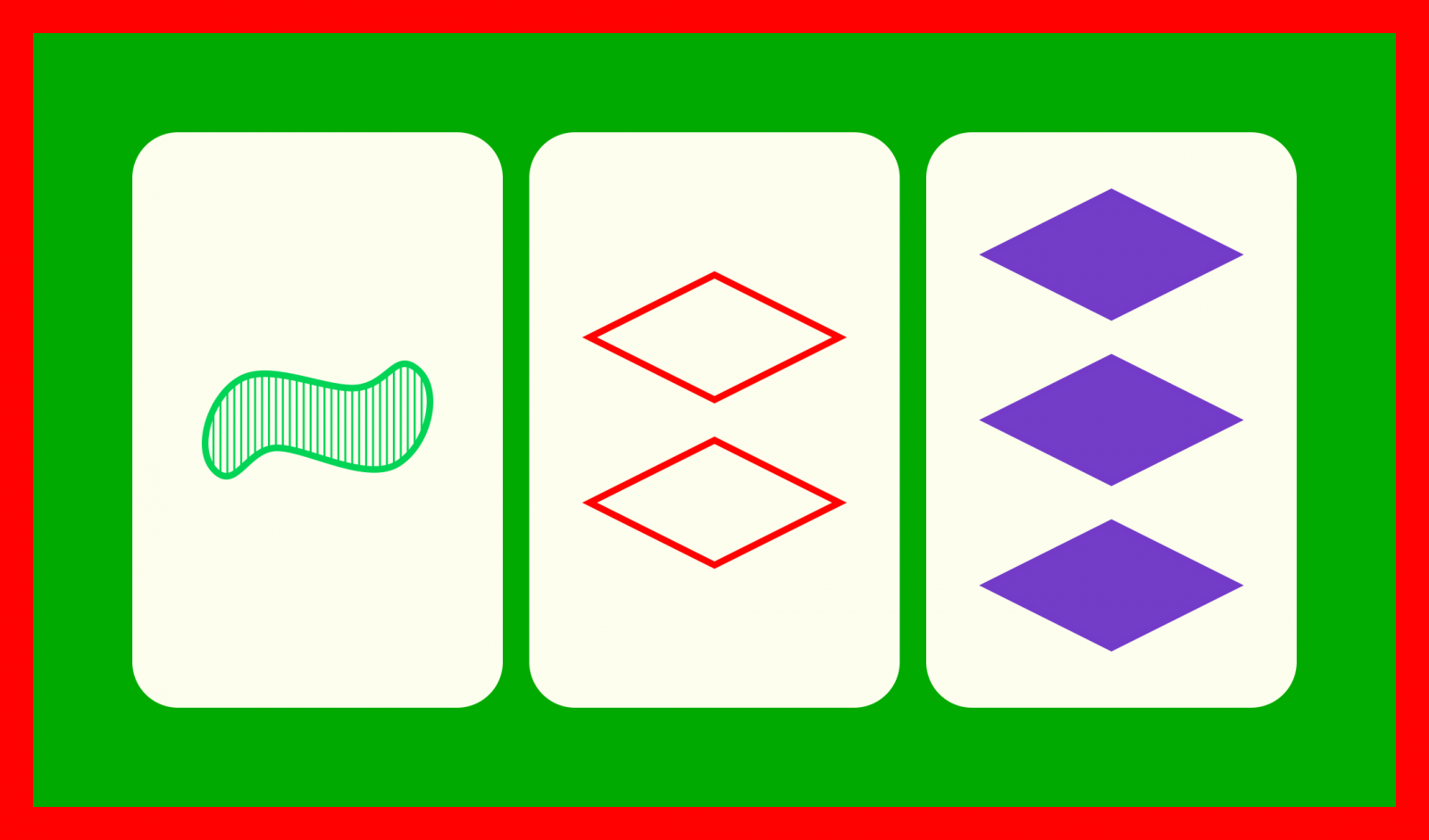
irudi desberdinak, kopuru desberdinak,
kolore desberdinak, betegarri desberdinak.
Ezaugarri berdinak eta ezaugarri desberdinak kontuan hartuz, lau SET mota daude. Hona hemen horien deskribapena:
1. mota: lau ezaugarriek agerpen desberdinak dituzte
Lehenengo karta aukeratzeko, 81 aukera daude.
Bigarren karta aukeratzeko, ezaugarri bakoitzeko 2 aukera daude, lehenengo kartan ez daudenak; beraz, guztira,
Hortaz, guztira, ![]() SET desberdin daude.
SET desberdin daude.
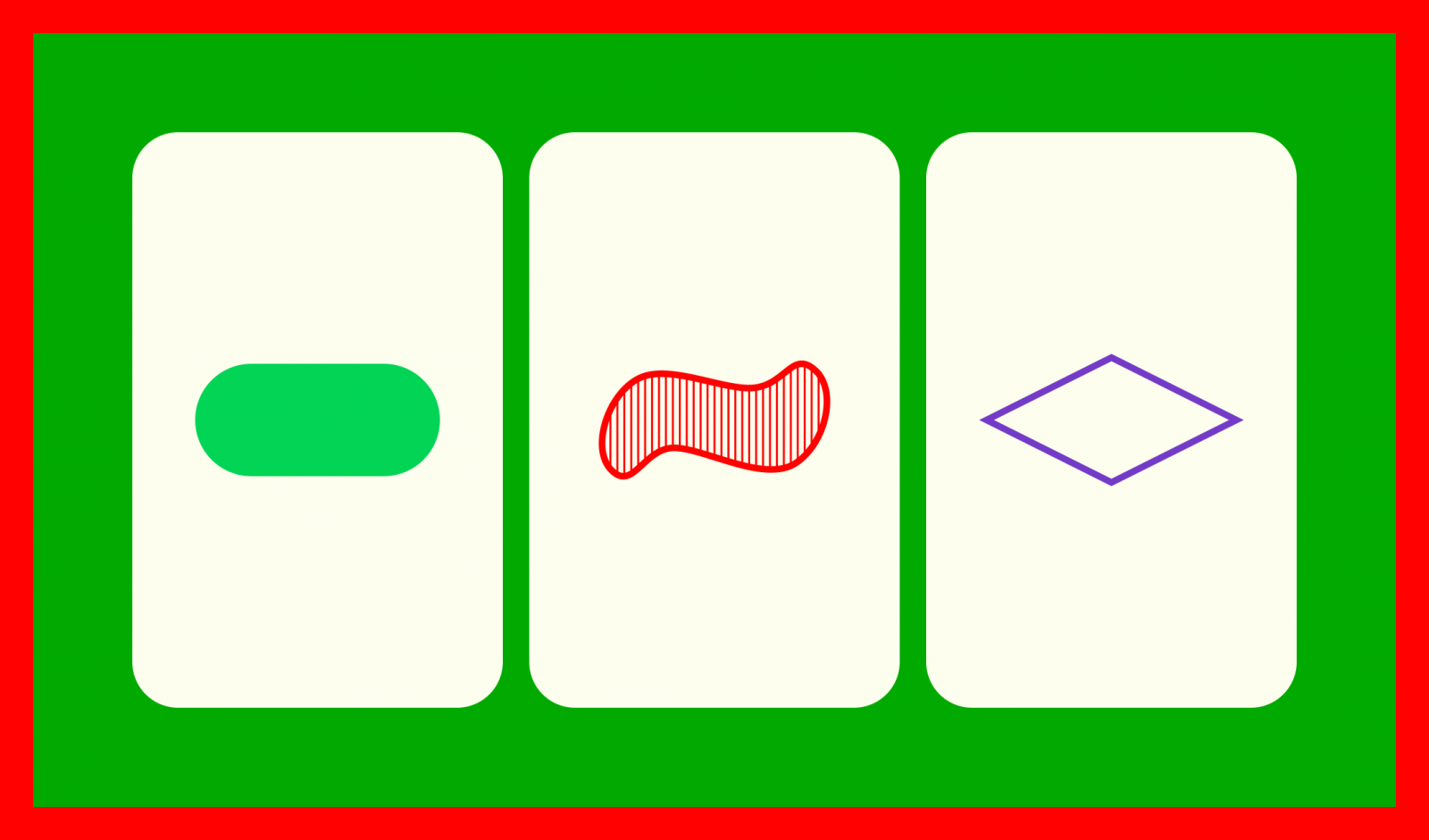
irudi desberdinak, kopuru berdina,
kolore desberdinak, betegarri desberdinak.
2. mota: hiru ezaugarrik agerpen desberdinak dituzte eta ezaugarri batek agerpen bera du
Agerpen bera izango duen ezaugarria aukeratzeko, 4 aukera daude.
Errepikatuko den agerpen hori aukeratzeko, 3 aukera daude.
Lehenengo karta aukeratzeko,
Bigarren karta aukeratzeko, geratzen den ezaugarri bakoitzeko 2 aukera daude, lehenengo kartan ez daudenak; beraz, guztira,
Hortaz, guztira, ![]() SET desberdin daude.
SET desberdin daude.

irudi desberdinak, kopuru berdina,
kolore desberdinak, irudi beteak.
3. mota: bi ezaugarrik agerpen desberdinak dituzte eta bi ezaugarrik agerpen bana dute
Agerpen bana izango duten ezaugarriak aukeratzeko, 6 aukera daude.
Errepikatuko diren bi agerpen horiek aukeratzeko,
Lehenengo karta aukeratzeko,
Bigarren karta aukeratzeko, geratzen den ezaugarri bakoitzeko 2 aukera daude, lehenengo kartan ez daudenak; beraz, guztira,
Hortaz, guztira, ![]() SET desberdin daude.
SET desberdin daude.

irudi desberdinak, kopuru berdina,
kolore berdina, irudi beteak.
4. mota: ezaugarri batek agerpen desberdinak ditu eta hiru ezaugarrik agerpen bana dute
Agerpen desberdinak dituen ezaugarria aukeratzeko, 4 aukera daude.
Errepikatuko diren hiru agerpen horiek aukeratzeko,
Lehenengo karta aukeratzeko, 3 aukera daude, hiru ezaugarri jadanik finkatuta daudelako.
Bigarren karta aukeratzeko, geratzen den ezaugarrirako 2 aukera daude, lehenengo kartan ez daudenak, hiru ezaugarri jadanik finkatuta daudelako.
Hortaz, guztira, ![]() SET desberdin daude.
SET desberdin daude.
Lau motak taula batean laburbilduz:
| Mota | SET kopurua |
| Lau ezaugarriek agerpen desberdinak | 216 |
| Hiru ezaugarrik agerpen desberdinak | 432 |
| Bi ezaugarrik agerpen desberdinak | 324 |
| Ezaugarri batek agerpen desberdinak | 108 |
| Guztira | 1.080 |
Iturriak
Dion Gijswijt: The card game SET: a mathematical challenge. https://diamhomes.ewi.tudelft.nl/~dgijswijt/papers/set-machazine.pdf
Jim Vinci: https://www.setgame.com/sites/default/files/teacherscorner/SETPROOF.pdf
Eskuko arauak: Devir.
Wikipedia (en)
