tangram jokoaren familia
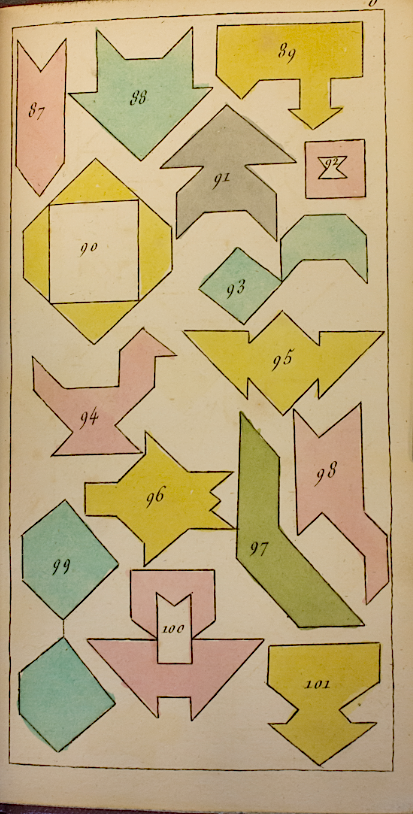
Le Véritable casse-tête,
ou Énigmes chinoises,
Paris, 1820.
British Library.
Disekzio-puzzleak ‒hainbat zatitan ebakitako irudi lau edo solidoak‒ jolas matematikoen forma zaharrenen eta ezagunenen artean daude. Ehunka daude, konplexutasun- eta dotorezia-maila desberdinetakoak. Arazoa beti da piezak lotzea, jatorrizko irudia, edo besteren bat, egiteko. Tangrama disekzio-puzzle guztien artean bikainena da.
Bitxia bada ere, ezer gutxi dakigu ziur tangramaren jatorriaz edo nork asmatu zuen. Tangram izenaren jatorria ere iluna da. Buru-hausgarria Txinan sortu zen ezpairik gabe. Erreferentzia zaharrena Kitagawa Utamaro-k (1753-1806) 1780an egindako zurezko grabatua da. Grabatu horrek bi gortesau irudikatzen ditu, qī qiăo băn (tangramaren izen txinatarra) ebazten saiatuz. Qī qiăo bănen zazpi piezak eguzkitik, ilargitik eta Marte, Jupiter, Saturno, Merkurio eta Artizarraren bost planetetatik hartu ziren.
XIX. mendeko buru-hausgarri txinatarrei buruzko liburu baten sarreran, tangram jokoaren jatorria (eta baita asmatzailea ere) ezezagunak direla irakur daiteke.
Tangram jokoaren izen txinatarra qī qiǎo bǎn (zazpi elementuen taula, edo jakituriaren taula, edo zazpi pieza argiak) da. Zhou garaikoa (o.a.a. 740-330) da hitza. Izena ohitura txinatar batetik dator. Izan ere, zazpigarren hileko zazpigarren egunean orratz baten zazpi zuloetatik hari bat pasatzeak zoriona omen zekarren.
Tangramari buruz argitaratutako lehenengo liburuak, Qing Xia Qing (1796-1820) enperadorearen garaian agertu ziren; lehenengoa 1813. urtean hain zuzen ere. Liburu horrek jadanik 300 irudi eman zituen. Liburuak aurreko urteko liburu bat aipatzen du, baina jokoa oso zabalduta zatekeen ordurako.
Liburu txinatarren edukiak bi zatitan banatu ohi dira. Lehenengoan, problemak planteatzen dira eta bigarrenean ebazpenak azaltzen dira. Problemek ikur txinatar bat eramaten dute irudiaren esanahia azaltzeko asmoz, batzuetan irudi hori laukia bezain abstraktua bada ere (ikus 2. irudia). Liburuetan ematen diren adibideak hainbat taldetan sailka daitezke. Irudi batzuek idazkera txinatarraren karaktere baten forma dute, eta azalpenik gabe agertzen ohi dira ezagunak direlako. Multzo handiena, ordea, gizakiek, animaliek, landareek eta objektuek osatzen dute, gaika antolatuta.
Jokoak arrakasta handia lortu bide zuen, 1813. urteaz geroztik argitaratu zen liburu-piloak adierazten duenez. 1820an argitaratutako Qi qiao zhou pien ho’pi liburuan oharpen hau agertzen da: “Liburu honetako sarrera eta adibideei laguntzen dizkieten testu argigarriak beste liburuetakoen desberdinak dira. Liburu honetako adibideak hobeak eta argiagoak dira. Mesedez, har ezazu kontuan.” Izan ere, maiz gertatzen zen irudiak ez zeudela arretaz aukeratuta eta batzuetan bi aldiz agertzen ziren.
Tangrama Europara eta Amerikara iritsi zen XIX. mendearen hasieran eta bere ospea gaur egun arte jarraitu du. Europan, esaterako, lehenengo lana Neues chinesisches Rätselspiel für Kinder, in 24 bildlichen und alphabetischen Darstellungen (Haurrentzako puzzle-joko txinatar berria, 24 irudirekin eta alfabetoaren ordenan) 1805. urtean agertu zela dirudi.

Bedside Book.
Entertainments for the Wakeful Hours
liburuko tangram-siluetak,
Edgar Cuthwellis, 1979,
Lewis Carroll eta Phuz-en ilustrazioekin.
British Library.
Europan eta Amerikan oso azkar zabaldu zen eta 1818. urterako jadanik aurki zitezkeen liburuak Alemanian, Austrian, Britainia Handian, Frantzian eta Italian. Frantzian, badirudi tangram bat Didot le Jeune inprentako Grossin-ek ekoitzia izan zela 1817an. Zazpi piezak ditu eta laurogeita bi konbinazio erreproduzitzen dituen liburu bat du lagun. Henry-René D’Allemagne-k (1863-1950) ez zuen ezagutzen, 1906an argitaratu zuen Récréations et passe-temps liburuan ez baitzuen aipatu, baina bai aipatu zuen 1818. urtean argitaratutako Allizeau-ren jokoa: joko hori bi karratuk eta hamabost piezek osatzen dute, eta, adibide gisa, 28 irudi proposatzen dira. Harrezkero, tangrama gero eta estimatuagoa izango da.
1817. urtean, W. Williams-ek New Mathematical demonstrations of Euclid rendered clear and familiar to the minds of youth, with no other mathematical instruments than the triangular pieces, commonly called the chineses puzzle (Euklidesen froga matematiko berriak, gazteen adimenari argi eta ezagun bilakatuak, pieza triangeluarrak baino tresna matematiko gehiagorik gabe, sarri buru-hausgarri txinatar gisa ezagutuak) izenburuko artikulu bat argitaratu zuen, zeinetan tangramaren laguntzaz ebatz daitezkeen zenbait ariketa matematiko aurkezten baita. Beste lan bat agertu zen, 1818an, Leipziger Magazin für Industrie aldizkarian.
Florentzian, 1818an argitaratu zen Al gioco cinese chiamato rompicapo (Buru-hausgarri izeneko joko txinatarra) liburuak jokoaren arauekin batera Txinaren historia bat dauka, eta esaten du leku guztietan jokatzen dela tangramean benetako grinaz.
Liburu europar eta amerikarrak, txinatarren kopiak izaten ziren gehienbat. Horren adibide gisa, AEBko Fashionable Chinese Puzzle liburua Britaniar Museoan dagoen Qi qiao zhou pien ho’pi liburu txinatarraren hitzez hitzeko kopia da. Liburu horietan indar gehiago jartzen da adibide txinatarren kopian, eta askotan gaizki ulertzen dira, esanahi propioa duten forma berrien sorkuntzan baino. Hala ere, tangram jokoari ekarpen bat egin zioten; letra eta zifra arabiarrena alegia. Ekarpen bat esan badugu ere, letra eta zifra hauen bertsio desberdinak egin ziren. XIX. mendearen hasieran agertu ziren liburuen artean Nouveau casse-tête français (Buru-hausgarri frantses berria) liburua nabarmentzen da bere irudi guztiak originalak direlako. Mende hasieran, irudiak liburu batean agertzen dira eta, mende bukaeran, irudiak orri soltetan agertzen dira eta denak kutxa batean.
Liburuen sarreretan jokoaren izaera matematiko-didaktikoa aipatzen da behin eta berriro. Hala ere, alderdi garrantzitsuena denbora-pasa unibertsala dela da. XIX. mendearen bukaeran eta XX. mendearen hasieran, Sam Loyd eta Henry Ernest Dudeney matematikari eta puzzle-sortzaileen arreta erakarri zuen. Loydek irudi berri asko asmatu zituen, agian Williamsen froga matematikoen laguntzarekin, eta The 8th Book of Tan (Tan-en 8. Liburua) idatzi zuen 1903an.
Louis Hoffmann-ek 1893ko liburuan ez du tangram izena erabiltzen puzzle honen berri ematen duenean, baizik eta The “Anchor” Puzzle izena, 63. orrialdean eta The Caricature Puzzle izena, 86. orrialdean. Azkenaren ondoko irudi-oin batean onartzen du garai hartan tangram izenarekin ezagutzen zirela eskuarki. Jokoa konbinazio-puzzleen atalean ematen du. Puzzle mota horietan irudi geometriko bat hainbat piezatan ebakita dago, jokalariak pieza horiek berrantolatu behar ditu bestelako irudia edo irudiak sortzeko. Tangram horiek harrizko gogortasuneraino trinkotutako konposizio mineralezkoekin egina daude, Anchor harrizko eraikuntza-bloke ezagunekin. Jokoaren kutxan, ohiko zazpi piezez gain, liburuxka txiki bat dago 150 irudirekin.

eskuz margotutako txartelak.
1870-870, Viktoriar garaia.
Worth Point.
Tangram izenaren jatorriaren atzean hainbat aieru dago. Alde batetik, gram bukaerak zerbait idatzita edo irudikatuta esan nahi du. Beste aldetik, hitzaren tan hasiera ez dago horren argi. Batzuen ustez, ingelesezko trangram (puzzle edo huskeria) hitzaren endekatze bat da; beste batzuen ustez, marinel amerikarrak entretenitzen zituzten Tanka nesketatik eratorria zen. Azalpen seguruena Tang dinastiaren izenetik etorritako hitza izatea da, hain ezaguna baitzen dinastiaren izena dialekto batzuetan "txinatarraren" sinonimo bihurtu zela. Hala bada, tangram "txinatar puzzlea" da.
Tangram jokoa ez da lehiaketarako jokoa; indibiduala baizik. Hala ere, azken urte hauetan tangrama bi jokalarien arteko lehia gisa planteatzen dituzten aldaerak argitaratu dituzte, irudiak osatzeko azkartasuna neurtzeko joko bezala.
Tangrama bi dimentsioko puzzlea da, baina ohiko puzzleetatik bi ezaugarrik bereizten dute: lehena, tangramean pieza kopurua eta piezen formak ez dira aldatzen; bigarrena, pieza horiekin hamaika irudi desberdin egin daitezke. Tangram jokoak oinarrizko forma geometriko kopuru jakin bat du, printzipio zaharraren arabera: baliabideak mugatzean ikusten da maisua.
Hasiera batean jokoaren xarmetako bat irudi berriak sortu ahal izatea bazen, pixkana xarma hori galduz joan zen (baina ez da oraindik erabat bukatu). Esaterako, Joost Elffer-en liburuan ematen diren ia 1600 irudietatik 750 egileek sortuak dira; gainerakoak iturri txinatarretatik eta europarretatik datoz.
Tangramaren xarma haren sotiltasunean datza. Zazpi pieza baino ez daude eta ahalik eta forma sinpleenetakoak dira. Jokoa zazpi pieza lauek osatzen dute, hala nola, bi triangelu txikik (berdinak), triangelu, karratu eta erronboide banak (bakoitza aurreko bi triangelu txikiez osa daitekeelarik) eta bi triangelu handik (lau triangelu txikiz osa daitezkeenak). Hala ere, zazpi pieza sinple horiek modu askotan elkartu daitezke. Joko honek ez duela araurik esan liteke. Hala ere, bi muga edo erregela baditu:
- Irudi guztiak zazpi piezekin osatu behar dira.
- Irudi guztiak lauak dira (ez dago piramideak egiterik)
Bi baldintza hauek errespetatuz, jokalariak nahi duena egin dezake fitxekin (adibidez, erronboidea bi aldeetatik erabil daiteke).
Gaur egun, oraindik ere, hainbat fabrikatzailek ekoizten dute. Boliak aspaldi utzi zion lekua egurrari, kartoiari, eta, orain, material plastikoei. Bukatzeko, tangram joko txinatarraren antza duten beste “tangram” jokoak ez direla falta esango dugu. Arauen atalean horien lagin bat ikus dezakezu.
Gauza gehiago esan bagenezake ere, tangram jokoa ondo ulertzeko onena jokoan aritzea dela uste dugu. Hementxe duzu jokoak eskaintzen dituen posibilitateen lagin txiki bat. Saia zaitez!

Osagaiak eta hasiera
Puzzlea zazpi piezek osatzen dute: bi triangelu zuzen txiki berdin, aurrekoekin osatutako karratu bat, triangelu zuzen ertain bat eta paralelogramo bat, lau triangelu txikirekin osatutako bi triangelu zuzen handi.
Bakar-jokoa da.
Helburua irudi desberdinak osatzea da.
Arauak
Irudi guztiak zazpi piezekin egin behar dira, ezin da pieza bat erabili gabe utzi.




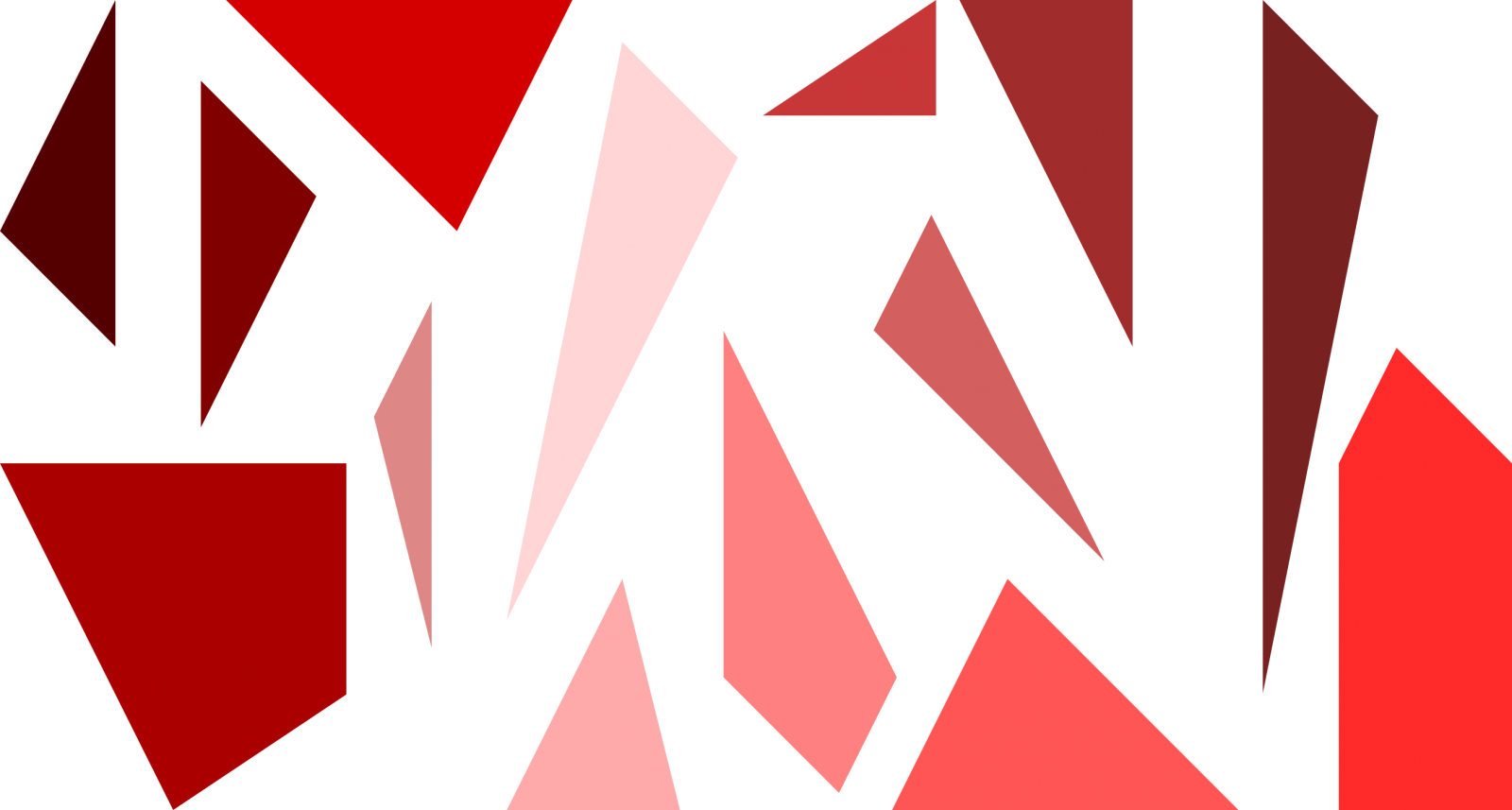
Disekzio-puzzle gehiago
Hainbat irudiko puzzleak
Ostomachion
Antzinako greziar geometrian, Ostomachion, Loculus Archimedius bezala ere ezaguna (latinezko Arkimedes-en kutxa) edo Syntomachion, Arkimedesi egotzitako tratatu matematiko bat da. Lan horrek bizirik iraun du, zatika, arabierazko bertsio batean eta antzinako grezierazko jatorrizko testuaren Arkimedes palinpsestoa izeneko kopia batean, bizantziar garaietan egina.
Ostomachion (Όστομάχιου) hitza grezierazko osteon (όστέου, hezurra) eta mache (μάχη, bataila, borroka) hitzetatik dator. Eskuizkribuan stomachion hitza dator, jatorrizko grezieraren ustezko endekatzea. Dezimo Magno Ausonio-k (Vasats, c. 309 – Bordeletik gertu, c. 394) ostomachion izen zuzena ematen digu. Ausoniok deskribatzen duen ostomachiona tangramaren antzeko buru-hausgarri bat zen, eta, agian, hezurrez egindako piezekin jokatu zuten. Ez dakigu zein den zaharragoa, Arkimedesen irudiaren azterketa geometrikoa, edo jokoa.
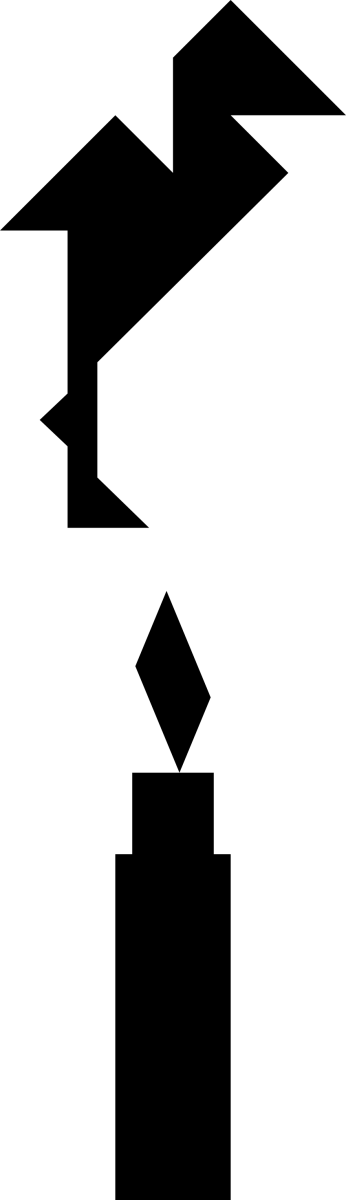
Puzzleak hamalau pieza ditu: hamaika triangelu, bi lauki eta pentagono bat.
Puzzlearen hasierako helburua pieza guztiekin karratu bat osatzea zen. Beranduago, piezekin osa daitezkeen hainbat irudi erantsiko ziren.

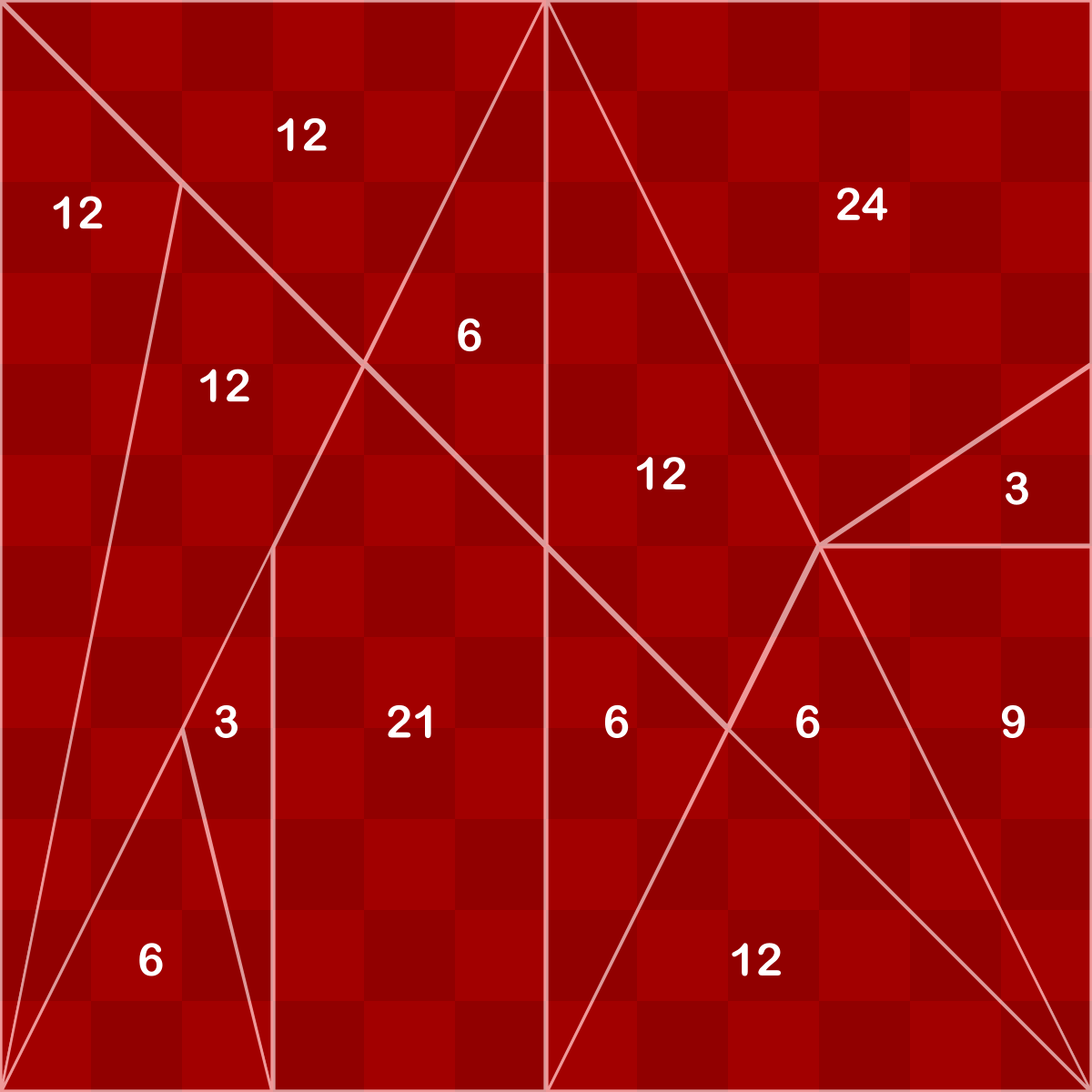
Karratua osatzeko, 17.152 soluzio daude; baina, simetriak, errotazioak eta islapenak kenduta, soluzio kopurua 268 da. Hamalau piezek osatzen duten karratuaren aldea 12 unitatekoa dela pentsatzen badugu, puzzlearen pieza guztien azalera zenbaki osoez adierazten dira, irudian ikusten diren balioak, hain zuzen.
.png)
Alle Neune (Bederatziak)
Bederatzi piezez osatutako puzzlea: zazpi triangelu (2, 2, 1, 1, 1) eta bi trapezio berdin. Laukizuzen bat osatzen dute. Hainbat irudi osatu behar dira.


Der Zornbrecher (Senetik atera)
Puzzle honen lehen adibide ezaguna 1892ko ekainekoa da eta urte hauetan gutxienez kaxa-estalkien lau diseinu ezberdin egon dira.
Zazpi piezez osatutako puzzlea: hiru triangelu (2, 1), bi lauki berdin eta bi pentagono irregular berdin. Oktogono bat osatzen dute. Hainbat irudi osatu behar dira.


Kreisrätsel (Zirkulua)
Puzzle honen lehen adibide ezaguna 1891ko abuztukoa da eta urte hauetan gutxienez kaxa-estalkien lau diseinu ezberdin egon dira.
Hamar piezez osatutako puzzlea: lau triangelu zuzen berdin eta sei triangelu lerromakur (2, 2, 2). Zirkulu bat osatzen dute. Hainbat irudi osatu behar dira.


Pentaminoa
Pentaminoen multzo osoa biltzen duen lehen puzzlea Henry Ernest Dudeney-ren The Canterbury Puzzles and Other Curious Problems liburuan agertu zen, 1907an argitaratua, The broken chessboard (Xake-taula puskatua) izeneko asmakizunean. Pentaminoen multzo osoa zuten laukizuzeneko lehen lauzak The Problemist Fairy Chess Supplement aldizkarian agertu ziren 1935ean, eta lauzatze-problema gehiago esploratu zituzten bertan, eta haren ondorengoan, The Fairy Chess Review aldizkarian.

.png)

egindako
irudiak.

egindako
irudiak.
Pentominoak Solomon W. Golomb-ek definitu zituen formalki 1953an. Poliminoen terminoa Golombek sortu zuen 1954an, American Mathematical Monthly aldizkarian argitaratu zuen Checker Boards and Polyominoes artikuluan. Beranduago, 1957an, Scientific American aldizkarian sakondu zuten azterketa. Polimino bat karratuen multzo konektatu bat baino ez da. Bi karratu konektatzen baditugu, domino bat lortzen dugu. Triminoak, hau da, hiru karratu konektatu, bi dira; tetraminoak, lau karratu konektatu, bost dira.
Martin Gardner-ek aurkeztu zituen, 1965eko urriko Mathematical Games zutabean, Scientific American aldizkarian. Golombek antzinako grezierazko πέντε (pénte) hitzatik pentamino terminoa asmatu zuen, bai eta domino hitzaren -ominoa ere, "d-" hori grezierazko di- (bi) aurrizkiaren forma bat balitz bezala interpretatuz. Golombek 12 pentominoak latinezko alfabetoko letren bidez izendatu zituen, FILiPiNo mnemonikoa alfabetoaren amaierako TUVWXYZ letrekin batera erabiliz.

Hamabi piezez osatutako puzzlea: pentamino bakoitza bost unitate-karratuz osatuta dago. Bost unitate-karratu elkartzeko hamabi forma desberdinak dira. Hainbat irudi osatu behar dira.
Hexiamanteak
Thomas O’Beirne-k (1910-1975) poliamanteak aztertu zituen, 1959an. Poliamanteetan hainbat triangelu aldekide lotzen dira. Esaterako, hexiamanteak sei triangelu aldekide elkartzean lortzen dira. Izena karta-sorta frantsesaren diamanteen serietik dator, diamanteak bi triangelu aldekidez osatuta daudelako.
Hamabi piezez osatutako puzzlea: hexamino bakoitza sei unitate-triangelu aldekidez osatuta dago. Sei unitate-triangelu elkartzeko hamabi forma desberdinak dira. Hainbat irudi osatu behar dira.
Hainbat irudi osa daitezke, hexamino guztiekin edo gutxiagorekin.


Tangram ez-simetrikoa
Vladimir Krasnoukhov-ek sortutako puzzlea da. Helburua bost piezekin irudi simetrikoak sortzea da.
Bost piezez osatutako puzzlea: bi trapezio zuzen berdinez osatutako bost pieza ez-simetriko. Hainbat irudi osatu behar dira.

Tangram arrauzkara
Puzzle honen lehen adibide ezaguna 1893ko irailekoa da. Beranduago hegaztien irudiak zituen liburuxka batekin argitaratu zen.
Bederatzi piezez osatutako puzzlea: hiru triangelu zuzen (2, 1), lau triangelu lerromakur (2, 2) eta bi lauki lerromakur berdin. Arrautza bat osatzen dute. Hainbat irudi osatu behar dira.


Tangram pentaminoa
Hamabi piezez osatutako puzzlea: hiru tetramino, lau pentamino, lau hexamino eta heptamino bat, unitate-karratuekin osatuak. Hainbat irudi osatu behar dira.

Arlekina
Henry Ernest Dudeney-k (1857-1930) The Canterbury Puzzles and Other Curious Problems liburuan aurkeztu zuen The broken chessboard (Xake-taula puskatua) asmakizuna, 1907an. Dudeneyk piezak alde batetik bakarrik margotu zituen; beraz, xake-taula osatzeko ezin ziren irauli.
Hamahiru piezez osatutako puzzlea: tetramino karratu bat eta hamabi pentaminoak. Pieza guztietan, karratuak bi koloretan daude margotuta, xake-taula osatzeko.
Xake-taula bat osatu behar da. Erronka horri baldintza bat erants dakioke, tetramino bakarra taularen zentroan kokatzea, hain zuzen. Baina, beste irudi batzuk ere osa daitezke, pieza guztiekin edo pieza batzuekin bakarrik. Esaterako, 3×3 karratua, 5×5 karratua, 4×5 laukizuzena eta 3×10 laukizuzena.
Bi irudiko puzzleak
Puzzle hauetan, puzzlearen pieza guztiekin bi irudi egin daitezke.
Dodekagonoa-karratua
Sei piezez osatutako puzzlea: triangelu aldekide bat, bost pentagono irregular berdin eta heptagono irregular bat. Dodekagono bat edo karratu bat osatu behar dira.

.png)
Izarra-karratua
Bost piezez osatutako puzzlea: bi triangelu aldekide, triangelu zuzen bat, lauki bat eta pentagono irregular bat. Sei erpineko izar bat edo karratu bat osatu behar dira.


Loreontzia-karratua
Hiru piezez osatutako puzzlea: zirkuluerdi bat eta bi triangelu lerromakur. Loreontzi bat edo karratu bat osatu behar dira.



Bestelakoak
Elfferen liburuan Michel Dekking-ek eta Jaap Goudsmit-ek tangramarekin egin daitezkeen irudi batzuk aztertu zituzten.
Tangram konbexuak
Tangram jokoaren piezekin infinitu irudi osa daiteke. Aski da horretarako irudi batean pieza bat pixka bat mugitzea. Baina jokoari seriotasun- edo zorroztasun-apur bat eman behar zaio.
Tangram jokoaren propietate interesgarri bat da jokoaren pieza guztiak ganbil edo konbexuak izatea. Irudia konbexua da bere barne-angelu guztiak 180º baino txikiagoak badira. Hauxe da orain galdera: Zenbat irudi konbexu eraiki daiteke tangramaz? Oraingoan erantzuna ez da infinitu irudi, ez. 1942. urtean, Zhejiang-eko Unibertsitate Nazionaleko Fu Traing Wang eta Zhu Xi Hsiung-ek frogatu zutenez, irudi konbexu hauek gehienez zortzi alde izango dituzte. Gero, irudi konbexuak laukizuzen baten barruan sartzen direla kontuan hartuz, 20 irudi konbexu sortzen zirela ere frogatu zuten. Horietatik 13 bakarrik eraiki daitezke tangrameko piezekin. Frogapen hauetan irudi konbexu hauek triangelu txikiak bezalako 16 triangelu erabiliz eraiki behar zirela pentsatu zuten; izan ere tangram jokoa 16 triangelu txikitan zati baitaiteke.
Sare-tangramak
Sare bat tarte erregularretan gurutzatzen diren harien multzo bat da. Sare-tangram bat zazpi piezen erpin guztiak sareko korapiloekin bat datozen tangramak dira.
Edozein sare-tangram oinarrizko triangeluekin zabal daiteke poligono konbexu bat lortu arte. Poligono konbexua lortzeko behar den oinarrizko triangeluen kopuru txikiena tangramaren konbexutasun-zenbakia da, eta tangrama barruan duen poligono konbexuari tangramaren edukitzaile konbexu. Esaterako, tangram konbexuek 0 konbexutasun-zenbakia dute eta beren buruaren edukitzaile konplexuak dira.
Bestalde, kontuan izanik tangram batean oinarrizko 16 triangelu daudela, oinarrizko 17 triangelu dituen poligono konbexu batetik oinarrizko triangelu bat ken daiteke eta tangram bat lor daiteke. Horrela lortuko genituzke 1 konbexutasun-zenbakia duten sare-tangram guztiak, 1-konbexuak. Ideia hori orokortuz, esan dezakegu irudi n-konbexuak lortzeko, nahikoa dela oinarrizko n triangelu tangramen 16 triangeluei eranstea.
Horrela, kalkuluak egin eta gero, oinarrizko 17 triangeluekin osatutako 9 poligono konbexu aurkitu ziren. Horiei oinarrizko triangelu bat ahal den modu guztietan kenduz, tangram 1-konbexuak lor daitezke. Eta 133 irudi 1-konbexu lortu ziren. Irudi 2-konbexuen kopurua oso handia da.
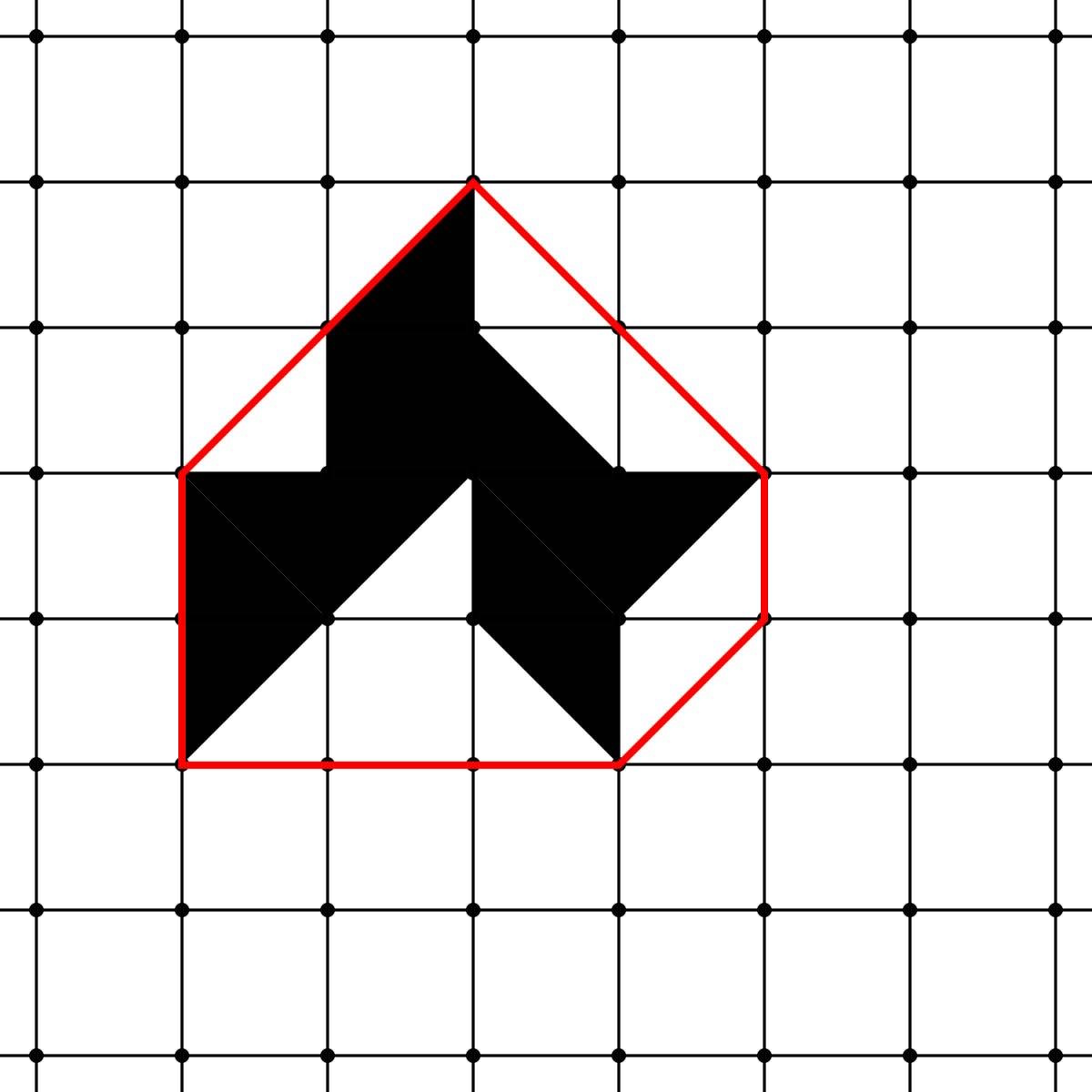
.png)
Konbexutasun-zenbakia handitu ahala, irudi kopurua ere handituz doa. Baina, irudi horietan tangramaren piezak bata bestetik urruntzen joaten dira. Ondorioz, tangramen osatzeak bere misterioa galtzen du. Egoera hori saihesteko, kontzeptu bat erabil daiteke, trinkotasuna. Tangram bat trinkoa dela esango dugu tangramaren edozein bi puntu lotzen dituen kurba tangramaren barrutik igarotzen denean. Kontzeptu horrekin, sare-tangram trinkoen konbexutasun-zenbakia mugatzen da. Egileek frogatu zuten sare-tangram trinkoen konbexutasun-zenbaki handiena 56 dela. Beste kontu bat da horrelako sare-tangram trinko bat eraikitzea; Rotterdam-eko bi ikaslek sare-tangram trinko 40-konbexua egitea lortu zuten.
Tangram zatigarriak
Izen honekin, sare-tangram trinkoaren piezak bi multzotan banatuz gero, multzo bakoitzeko piezekin irudi berdinak osatuz lortzen diren tangramak izendatzen dira. Hortaz, Tangram zatigarria bi erdi berdin-berdinen konbinazioak dira. Irudi biki horien kopurua 65 da. Irudi bikiak elkartzeko aukerak ugariak direnez, sare-tangram trinko zatigarriak hamaika dira.

Iturriak
Patxi Angulo martin. Jolas Matematikoak. Tangram-a. Elhuyar, Usurbil, 1990.
Joost Elffer: El Tangram. Editorial Labor S.A., Bartzelona, 1982.
Joost Elffer eta Michael Schuyt: Tangram. El antiguo rompecabezas chino. Evergreen, Kolonia, 1999.
Louis Hoffmann: Hoffmann's Puzzles Old & New. Frederick Warne and Co. and New York, Londres, 1893.
Jean-Marie Lhôte: Histoire des jeux de société. Flammarion, Paris, 1994.
Jerry Slocum eta Jack Botermans: Puzzles, old & new. 1987.
Juegos de Ingenio (2). RBA, Bartzelona, 2003.
https://gallica.bnf.fr/ark:/12148/bpt6k33574949/f210.item
https://gutenberg.org/cache/epub/27635/pg27635-images.html#s74
