bakar-jokoa
Hipotesi desberdinak daude joko honen jatorriaren inguruan. Bakar-jokoaren jatorriari buruzko iradokizunik ausartena, agian, Becq de Fouquières-ena (1831-1887) da, Ovidioren (o.a.a. 43 - o.a. 17) Ars Amatoria (Maitatzeko artea) laneko pasarte baten subjektua izan zela uste baitu:
reticuloque pilae leves fundantur aperto
nec, nisi quam tolles, ulla movenda pila est
Pasarteak bost joko deskribatzen ditu laburki, neskentzat egokiak diren denbora-pasa gisa: dadoak, latrunculi, pilae leves, duodecim scripta eta hiru lerro batean. Peter Green-ek, bere ingelesezko itzulpenean, honela dio: "Hirugarrena, dado eta taula motako jokoen segida horretan, hain dago tokiz kanpo, ezen batek pentsa dezakeela testua transposizioa edo interpolazioa izan daitekeela. Deskribatzen duena sare batean husten diren ‘bola lau’ batzuk dira, helburua izanik bat mugitzea gainerakoak nahasi gabe. Hori nola egiten zen ez dago batere argi. Spillikins (mikado antzekoa) izenez ezagutzen den haurrentzako joko ezagun eta ulergarriagoa iradokitzen du.”
Becq de Fouquièresek, bere desegokitasunaz ere ohartuz, honela interpretatzen du pasartea: “Ovidiok dio: bola txikiak (pilae leves) taula (reticulo) bateko zuloetan jartzen dira baten aurrean, eta bola bat ere ezin da altxatu harrapaketarik egiten ez badu (nisi quam toiles).” Hau da, bakar-jokoa.
Pasarte horren kontra, Bodleian Library-ko kopian, arkatz-ohar bat idatzi zuen H. J. R. Murrayk, eta, noski, ez dator bat haren ondorioarekin, eta aukera gisa galdetzen du “ziriak (spilikins ~ mikado) bezalako jokoren bat?”.
Bakar-jokoaren jatorria klerigoei ere esleitu zaie, priesterspiele (apaizen jokoa) eta nonnenspiele (mojen jokoa) izen alemanek iradokitzen duten bezala, nahiz eta grillenfang (kilkerren harrapaketa) ere deitzen zioten, arrazoi beragatik matxinsaltoen asmakuntza iradokiz. 1799ko Encyclopédie Méthodique-k dio amerindiarrek geziekin jokatu zutela lehenago, ehizatik itzuli ondoren.
Joseph Strutt-ek hipotesi ezagunena azaltzen du: "Esaten da zorigaiztoko gizon batek asmatu zuela, hainbat urtez Bastillan isolatuta egon zena Parisen, eta joko zahar baten (azeria eta antzarak jokoaren) taulaz baliatu zela. Baina, joko horren taulak 33 posizio izaten ditu eta bakar-joko frantsesaren taulak 37 posizio; ez datoz bat, beraz.

Bitxiagoa da 1986ko egunkari alemaniar batek artzai malgaxeei esleitu izana, jokoa oso zabalduta baizegoen.
Berez, badirudi bakar-jokoa XVII. mendean agertu zela Luis XIV.aren gortean, mende horretako azken hamarkadako hainbat grabatutan irudikatuta izanik. Horietako batean, 1697an, Claude-Auguste Berey-k Madame la Princesse de Soubize jouant au jeu de solitaire irudikatu zuen bakar-jokoan hastear zela. Irudian 37 zuloko taula frantsesa ikus daiteke.
Jokoa XVIII. mendean igaro zen Ingalaterrara, izugarrizko oihartzuna lortu zuelarik, eta taula propioa eratu zuten, 33 posiziorekin.
Bakar-jokoaren taula azeria eta antzarak joko zaharrenerako eta haren baliokideetarako erabiltzen zen taula bera denez, haiek ere errota eta alkerke jokoetatik eratorritako tauletan jokatuta, bakar-jokoa azeria eta antzarak norberak jokatzeko saiakera batean sor zitekeen.
33 zuloko taula 1779an aipatu zuen lehen aldiz J.C. Wiegleb-ek Unterricht in der natürlichen Magie (Magia naturalaren ikasgaiak) lanaren I. bolumenean, 37 eta 45 zuloko taulekin batera (azken hori beso bakoitzean sei zulotik bederatzira igoz lortua).
Matematikariak jokoaz interesatu zirenaren frogak baditugu. 1985ean, John Beasly-k The Ins and Outs of the Peg Solitaire liburua argitaratu zuen. Jokoaren jatorriari eskaintzen dion kapituluan, Gottfried Leibniz-ek (1646-1716), 1710ean, Berlingo Zientzia Akademiarako idatzitako artikulu bat aipatzen du. Honela hasi zuen:
Duela gutxi, Solitarium izeneko joko-mota bat zabaldu zen, nire kasa jokatzen dut, baina lagun batekin lekuko eta arbitro gisa arituko balitz bezala.
Beste froga bat Leibnizek Pierre Rémond de Montmort-i 1716an idatzi zion gutuna da. Edouard Lucas-ek (1842-1891) bere Récréations Mathématiques liburuan kapitulu bat eskaini zion joko honi, bukaera desberdinei buruzko ariketak proposatuz.
Bakar-jokoaren ingelesezko lehen estudio serioa 1920an egin zuen Ernest Bergholt-ek. Complete Hand-book to the Game of Solitaire on the English Board of Thirty-three Holes (33-zuloko taula inegeleseko bakar-jokoaren eskuliburu osoa) lanean Bergholtek berak "ia ikerketa-eremu birjina" zeritzona zabaldu zuen, eta merezi gabeko utzikerian erori zela deitoratu zuen, “orain arte inork ez baititu inoiz ikertu gaiaren aukerak, edo adimen ertaineko pertsonari jokoak zabaltzen dizkion problema ugari eta liluragarriei buruzko gida egokirik eman”.
1953an, Alan Turing matematikari eta informatikaren sortzeaileak zortzi urteko neskato Maria Greenbaum-i bakar-jokoa azaldu zion, eskutitz batean.
Laburbilduz, jokoa mundu osoan ezaguna dela esan daiteke. Garai batean bakar-jokorako taula, hala egurrezkoa nola bolizkoa, landua zein apala, ez zen falta harrera-geletan. Denboraldi batean baztertuta egon ondoren, gaur egun berpiztu egin da zaletasuna. Bestalde, denda askotan ikus daitezke landutako diseinuko taulak. Horrez gain, ohiko jokoaz aparte, problema asko sortu dira taula berean eta arau berdinekin.
Jokoaz
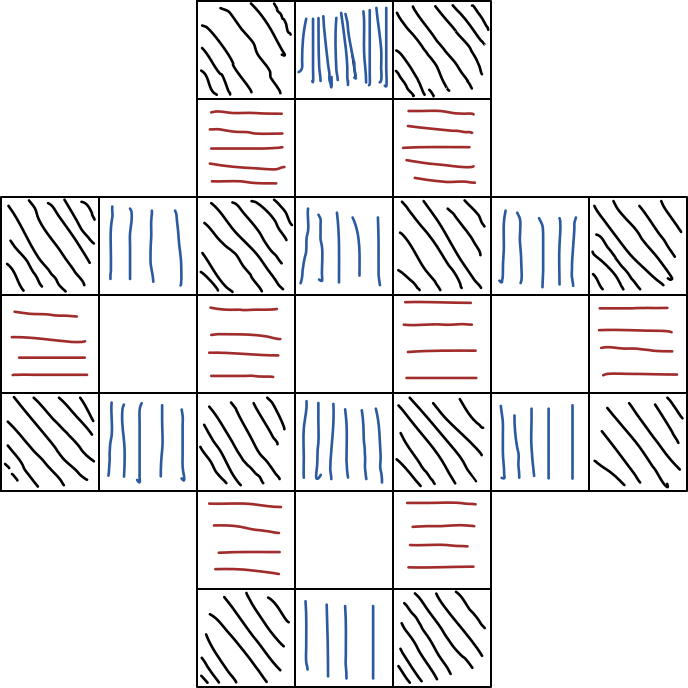
Lau fitxa mota bereizten dira posizioaren arabera; izan ere, fitxa guztiak berdinak diruditen arren, benetako jokoan, harrapaketa bidezko mugimenduaren prozedurak hogeita hamahiru zuloen azpimultzo batera mugatzen du edozein fitxaren mugimendua, xakean jokalari baten alfil baten mugimenduak taulako hogeita hamabi laukira mugatzen diren bezala. Bakar-jokoan, Alan Turingen eskema erabiliz, marra zeihar beltzez agertzen diren posizioetan dauden fitxak hamabi zuloren gaineko mugimendura mugatuta daude; marra bertikal urdinez eta marra horizontal gorriz agertzen diren posizioetan dauden fitxak zortzi zulotara baino ez dira iristen, eta zuriz agertzen diren posizioetan dauden fitxak, berriz, bost zulotara baino ez (bederatzi taula frantsesean). Lau fitxa mota horiek lau zirkuitu independente dute mugitzeko eta fitxa bat ez da inoiz aldatuko zirkuitu batetik beste batera.
Helburua erdian bukatzea bada, bost fitxa berdeak jokoan zehar ez harrapatzeaz arduratu behar da, horiek baitira erdira irits daitezkeen fitxa bakarrak. Beste muturrean, nahiko erraza izan behar luke hasieran fitxa hori batek betetzen duen zuloetako bat xede gisa ezartzea, betiere jokoan zehar hori guztiak ez kentzeko kontuz ibili behar baita. Hasiberriak aurreko eskemaren arabera markatu edo koloreztatutako fitxekin jokatuz has daitezke, pistari jarraitzen laguntzeko.
Ohiko jokoan, jokalariak hogeita hamahiru fitxetako bat kentzen du taulatik eta, ondoren, gainerako hogeita hamabi fitxak harrapatuz aterako ditu taulatik. Harrapaketa bat fitxa bat aldamenean dagoen beste fitxa baten gainetik jauzi eginez egiten da, atzean dagoen zulo hutsera eramanez, dametan bezala. Helburua fitxa guztiak taulatik ateratzea da, azkena izan ezik, jakina, eta hori egin behar da halako moldez non azken fitxak hasiera batean hutsik geratu den zuloa betetzen duen. Zaila izaten denez oroitzea zer zulo utzi den hutsik partida hasieran, ohikoa izaten da zentroko zuloa hustea. Horrez gain, edonondik has daiteke fitxa kentzen eta zentroko zuloan bukatu; edo, errazago egiteko, edonon hasi eta bukatu erdialdeko bederatzi zuloetako batean. Izan ere, asmakizunen eta problemen sorta zabala asmatu da; haien helburuek eta baldintzek trebetasuna eskatzen dute jokoaren planifikazioan.

https://www.grenierdenfance.be
Ikusgarrietako batek man on the watch (gizona zain) izena du. Horretan jokalariak aurretik esaten du zein izango den azken fitxa taula gainean, eta baliteke fitxa hori ez mugitzea harrapatzeko mugimenduen azken segida egiteko prest dagoen arte. Helburu gehigarri bat azken segida hori ahalik eta luzeena egitea izan daiteke. Beste ikuspegi bat, colourtaire (kolorezko bakar-jokoa) izenekoa, fitxak kolorearen arabera bereiztea da, eta koloreak ordena jakin batean kentzeko hasierako diseinuak zehaztea. Jokoaren aldaera agerikoa eta maizen agertzen dena geratzen diren fitxak aurrez zehaztutako egitura bat osatuz uzteko helburua duena da.
Bakar-jokoa taula askotan joka daiteke, karratua, hexagonala, triangeluarra… Beaslyren ezinbesteko lanean agertzen dira aztertuak izateko interes berezia zuten joko oso ezagunak.
Bestalde, saiakerak egin dira bakar-jokotik bi jokalarirentzako joko bat sortzeko. Lehen hurbilpen arraza izan daiteke esatea jokalari bakoitzak fitxa bat mugitzen duela bere txandan, jokalari batek mugitu ezin duen arte eta, beraz, galduz. Irabazleak puntu bana jasoko du taula gainean geratzen den fitxa bakoitzeko. Partida bat aurretik zehaztutako puntuak lortu arte joka daiteke.
David Ramsay-ren interruption (eten) jokoan, lehenengo jokalaria hasten da fitxak banan-banan kentzen. Bigarren jokalariak edozein unetan eten dezake jokoa, eta ahalik eta fitxa gehien kendu behar ditu taulatik. Berriro ere puntu-sistema erabil daiteke; demagun bigarren jokalariak n. mugimenduaren ondoren eten duela eta m fitxarekin amaitzen duela taulan; bere puntuazioa n−m izan daiteke.
Jokoa interesgarriago egin daiteke, fitxak bereiziz jabetzari edo berezko balioari dagokionez, edo biak. Joko horietako asko asmatu dira, baina bakar bat ere ez da iritsi klasiko baten egoerara.
Bakar-joko ingelesa
Hemen bakar-joko ingelesaren arauak emango ditugu. Gainerako aldaeretan fitxen mugimendua berdina da.
Osagaiak eta hasiera
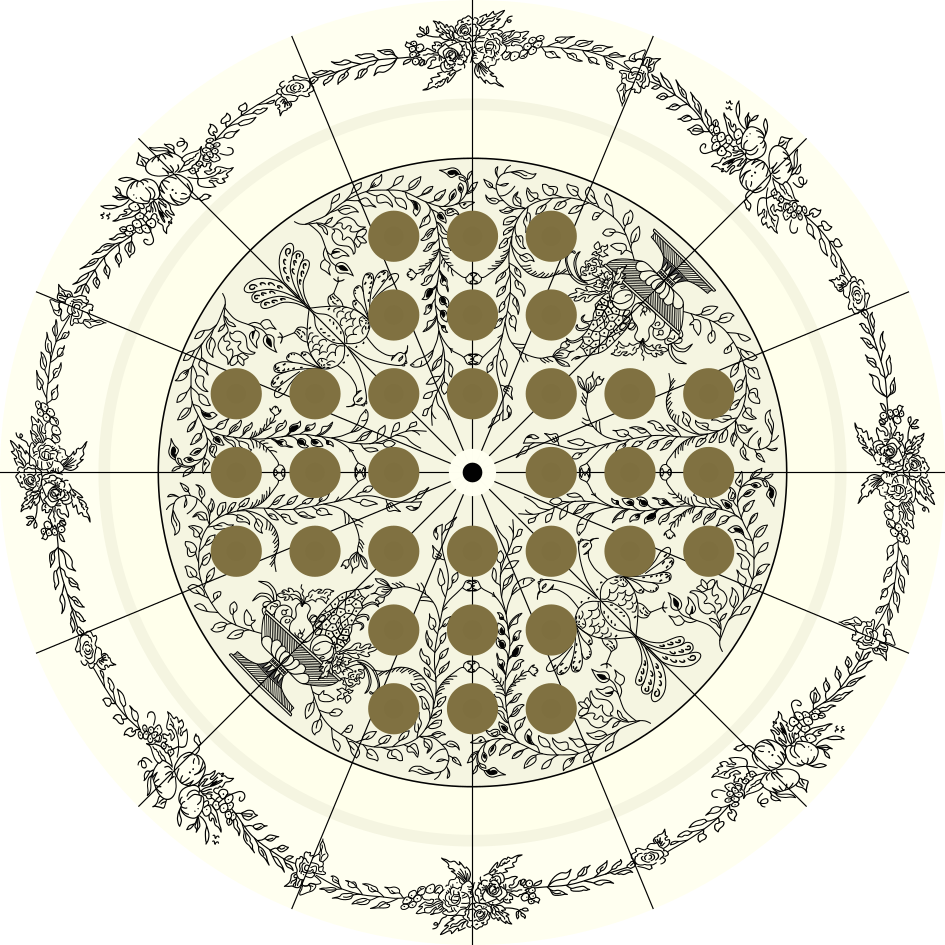
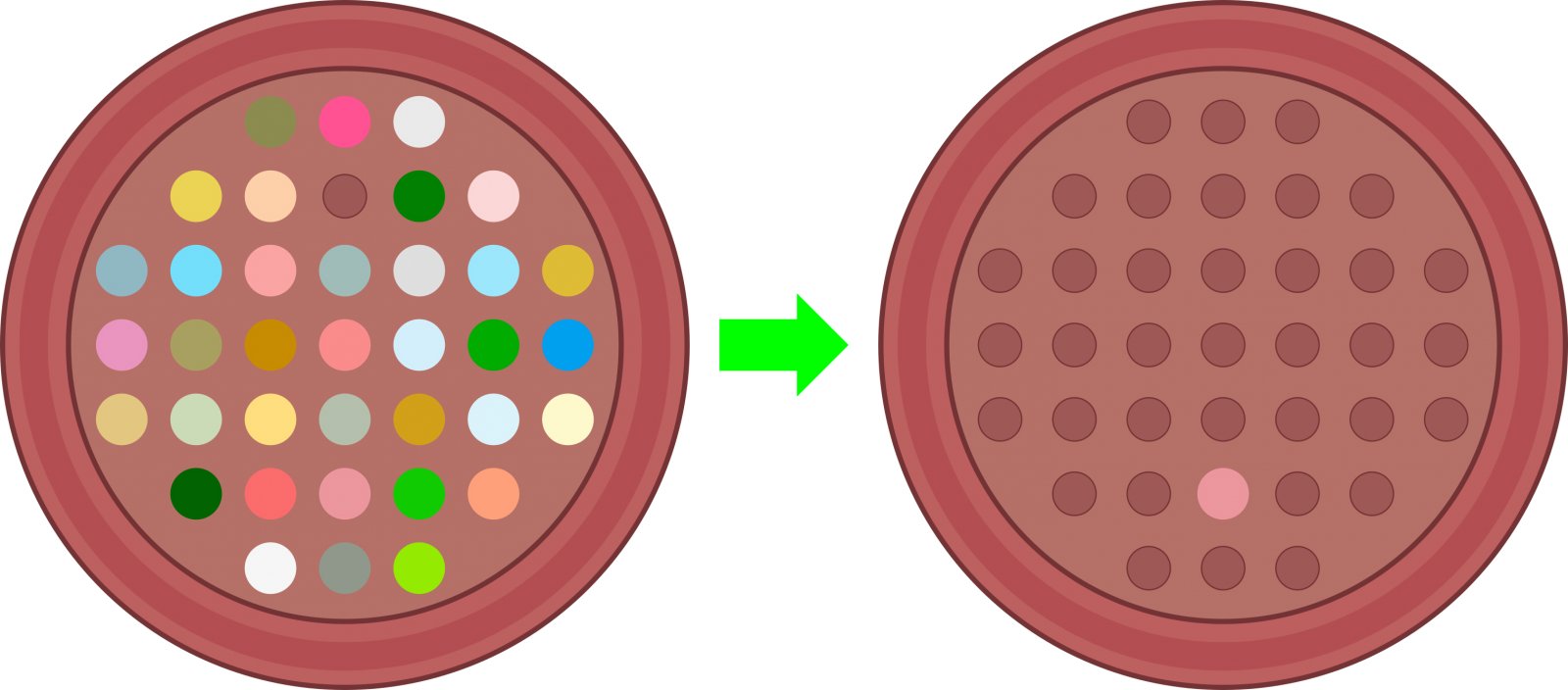
Taula gurutze-itxurakoa eta 33 zuloz osatua da.
32 fitxa (bolak, ziriak…) kokatzen dira zuloetan, zentroa hutsik utziz.
Helburua zentroko zuloan fitxa bakar bat uztea da.
Arauak
Fitxa bat ezin da mugitu, jauzi egin ezean. Jauzi hori ondoko fitxa baten gainetik egin behar da segidan dagoen zulo huts batera, eta jauziak ortogonala izan behar du --ezkerrera, eskuinera, gora edo behera--, inoiz ez diagonala. Gainditutako fitxa berehala aterako da taulatik.
Aldaerak
Praktikatzen
Praktikatzeko asmoz, ariketa moduan hasierako posizio sinpleago batzuk eman daitezke fitxa gutxiago jarriz taulan. Adibidez, 6 fitxa gurutze bat osatuz; edo 16 fitxa triangelu bat osatuz.
- 9 fitxa gurutze grekoa osatuz, taularen zentroan.
- 11 fitxa goiko adarrean jarrita, zentro bete gabe.
- 21 fitxa egitura simetriko bat osatuz.


Hasiera desberdina
Zentroko fitxa kentzearena ez da beti izan lehenengo aukera. Kasu batzuetan nahi zen fitxa kentzen zen jokoan hasteko.
- Taula osoa fitxaz bete eta kendu nahi duzun fitxa. Azkeneko fitxa libre utzi duzun zuloan utzi behar da.
- Taula osoa fitxaz bete eta kendu nahi duzun fitxa. Azkeneko fitxa taularen beste posizio batean edo zentroan utzi behar da.

bakar-jokoaren taula.
Kanaria uharteak.
Taula aldatuz
Aipatutako taula bakar-joko ingelesarena da, baina badaude beste taula batzuk ere:
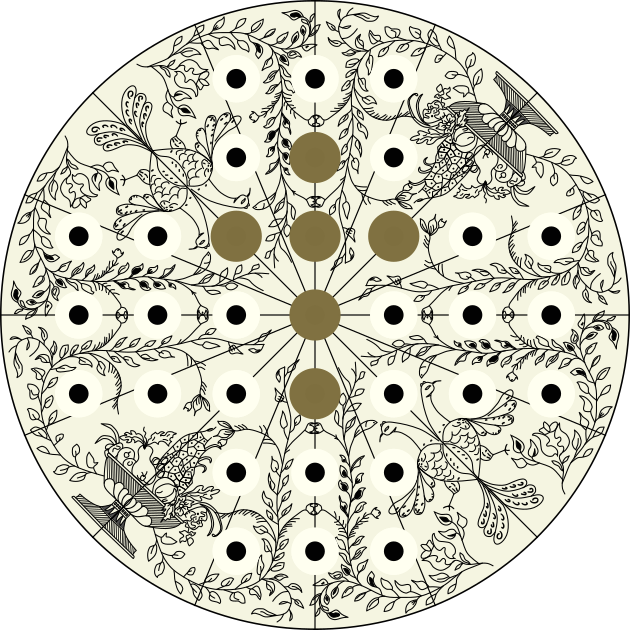
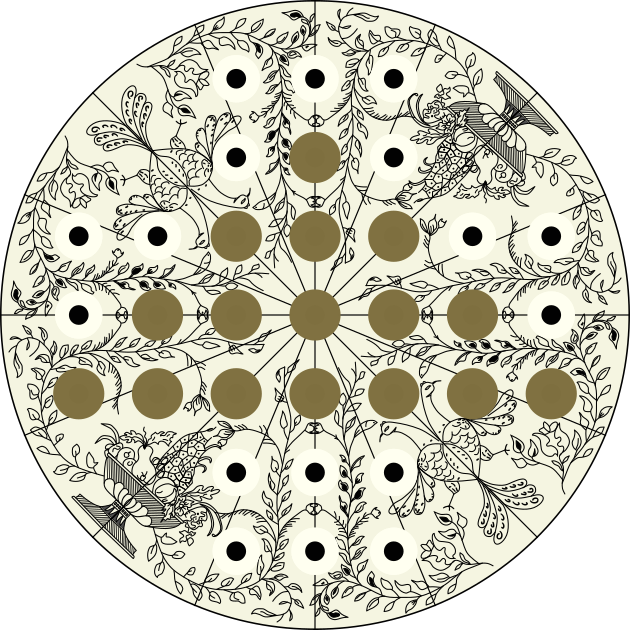
- Bakar-joko frantsesa: gurutze-itxurakoa eta 37 zulokoa (a irudia).
- Wiegleb-en 45 zuloko taula, 1779 (c irudia).
- Bakar-joko erronbikoa: erronbo-itxurakoa edo karratu bat erpin baten gainean jarrita, 41 zulo (d irudia).
- Bakar-joko triangeluarra: triangelu-itxurakoa eta hainbat zulotakoa (e, f irudiak). Azkeneko fitxa goiko erpinean utzi beharko da.
.png)
Helburua aldatuz
Jokoaren helburua ere alda daiteke, bukaera desberdinak bilatzearren. Fitxa guztiak jartzen dira taulan, zentroan izan ezik. Fitxak kentzen joango gara, baina fitxa batzuk taulan utziko ditugu egitura desberdinak osatuz:
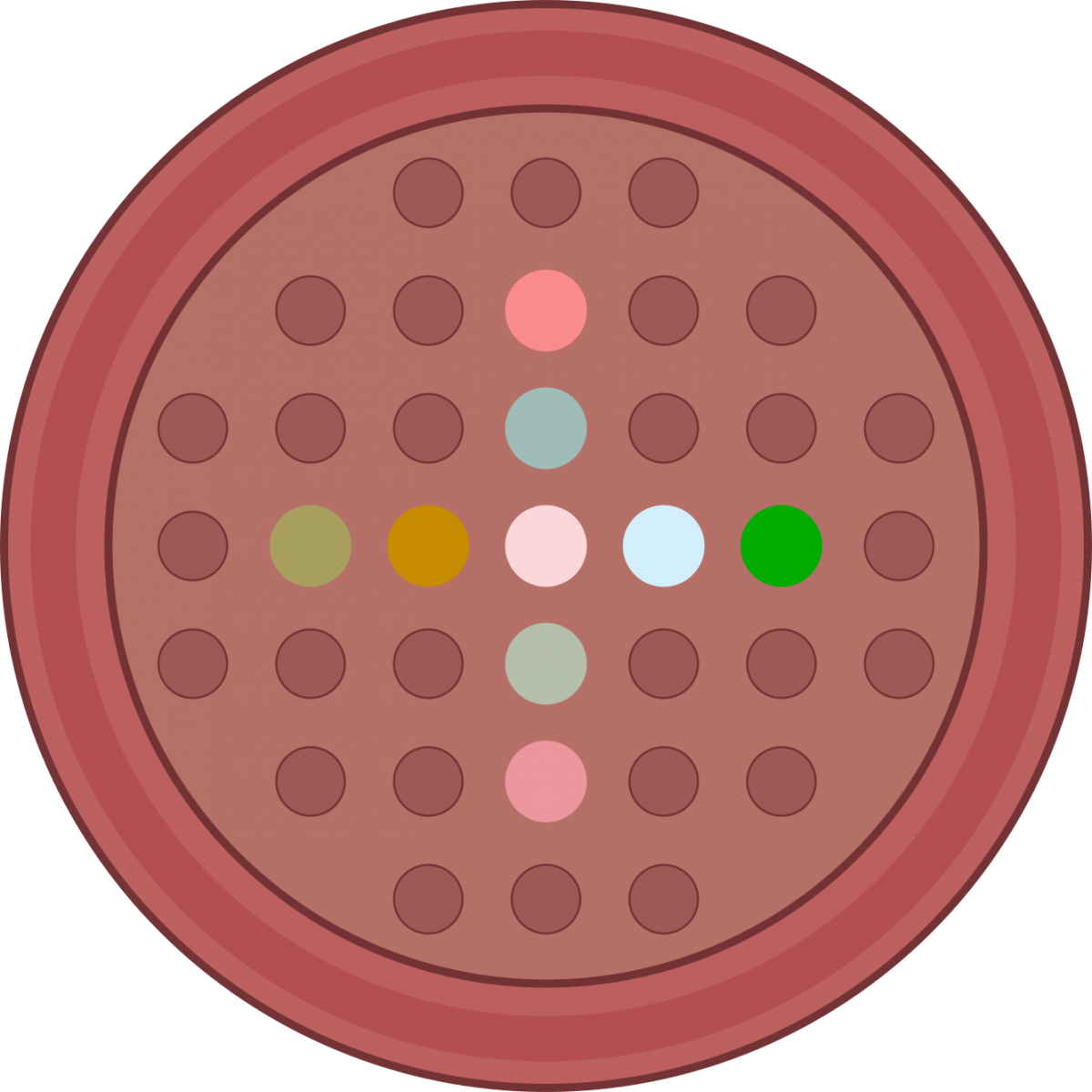
- San Andresen gurutzea: erdialdean 5 fitxa utzi San Andresen gurutzea osatuz.
- Gurutze latindarra: erdialdean 6 fitxa utzi gurutze latindarra osatuz.
- Errotaren gurutzea: 12 fitxa utzi errota baten gurutzea irudikatuz.
- Gurpila: ertzeko zulo batzuetan eta zentroan 13 fitxa utzi behar dira.
- E letra: 13 fitxa utzi behar dira bukaeran E letra osatuz.
- Triangelu handiena: 16 fitxa utzi triangelu bat osatuz.
- Zirkunferentzia: ertzeko zuloetan eta zentroan 17 fitxa utzi behar dira (4. irudia).
- ϴ egitura: 21 fitxa utxi behar dira bukaeran ϴ egitura osatuz.






Leap-frog (jauzi-igela, txorro-morro)
H. J. R. Murrayk bakar-jokoaren sailean ematen duen jokoa, eta arauak.
Osagaiak eta hasiera
Taula, eskuarki, 15×15 eta 18×18 laukikoa da.
Lauki bakoitzean fitxa bat dago, guztira 225 eta 324.
Nahi adina jokalarik hartuko dute parte.
Arauak
Fitxa bat aldameneko beste fitxa baten gainetik jauzi eginez mugituko da, fitxaren beste aldean dagoen lauki huts batera; gainditutako fitxa taulatik ateraz. Jauzia ortogonalean egingo da, ez diagonalean.
Txandaka, jokalariek fitxa bana aterako dute taulatik.
Ondoren, txandaka, jokalariek harrapaketa bat edo harrapaketa-segida bat egingo dute.
Hainbat harrapaketa egin badaitezke, horiek joko-txanda berean egingo dira.
Jokoa bukatuko da harrapaketa gehiagorik ezin denean egin.
Fitxa gehien harrapatu duen jokalariak irabaziko du.
Soluzioa
Jokoaren azterketa sakona ezagutzen da (Winning Ways for your Mathematical Plays). Analisi horrek pagoda funtzio izeneko nozioa sortu zuen. Funtzio hori tresna indartsua da bakar-jokoaren problema jakin baten, orokor baten, eginezintasuna erakusteko. Pagoda funtzio bat aurkitzeko soluzioa programazio linealeko problema gisa formulatzen da, eta denbora polinomioan ebatz daiteke (Integer Programming Based Algorithms for Peg Solitaire Problems).
1990eko artikulu batean, bakar-jokoaren ploblemen baliokideak diren Hi-Q problema orokorrak aztertu ziren, eta beren NP-osotasuna agertu zen (Generalized Hi-Q is NP-complete).
1996ko artikulu batek bakar-jokoaren problema bat konbinatoriaren optimizazio-problema gisa formulatu zuen, eta bakar-jokoaren kono izeneko eskualde egingarriaren propietateak eztabaidatu zituen (On the solitaire cone and its relationship to multi-commodity flows).
1999an, bakar-jokoa erabat ebatzi zen ordenagailu batean, aldaera guztien bidezko bilaketa zehatza eginez. Simetriak, taula-konstelazioen biltegiratze eraginkorra eta hashing erabiliz lortu zen (Spielverderber, Solitaire mit dem Computer lösen).
2001ean metodo eraginkorra garatu zen bakar-jokoaren problemak ebazteko (Integer Programming Based Algorithms for Peg Solitaire Problems).
Aljebra abstraktua erabiliz froga daiteke taulako 5 posizio finko baino ez daudela, non jokoa arrakastaz amai daitekeen fitxa batekin (Mathematics and brainvita).
Hona hemen jatorrizko jokoaren soluzio bat:

irizpidearekin zenbakituak.
| Txanda | Mugimendua | Txanda | Mugimendua | Txanda | Mugimendua |
| 1. | 24→44 | 12. | 56→54 | 23. | 52→32 |
| 2. | 32→34 | 13. | 75→55 | 24. | 32→34 |
| 3. | 13→33 | 14. | 73→75 | 25. | 34→36 |
| 4. | 15→13 | 15. | 45→65 | 26. | 36→56 |
| 5. | 43→23 | 16. | 75→55 | 27. | 56→54 |
| 6. | 13→33 | 17. | 25→45 | 28. | 44→42 |
| 7. | 63→43 | 18. | 37→35 | 29. | 64→44 |
| 8. | 51→53 | 19. | 57→37 | 30. | 45→43 |
| 9. | 31→51 | 20. | 34→36 | 31. | 42→44 |
| 10. | 54→52 | 21. | 37→35 | ||
| 11. | 51→53 | 22. | 54→52 |
Eskuineko taulan soluziora eramaten duen aukera baten mugimenduak daude. Gezi berdeek adierazten dute mugimendua bertikalean egin behar dela taulan, eta gezi gorriek mugimendua horizontalean egin behar dela; bi zenbakien artean dagoen zenbakiko posizioko fitxa taulatik kendu behar da urratas bakoitzean.
Hans Zantema
Bakar-joko frantsesa
Joko honek ez du soluziorik, jatorrizko bertsioan, hau da, hasieran zentroko zuloa libre uzten badugu eta azken fitxa zentroan utzi nahi badugu.
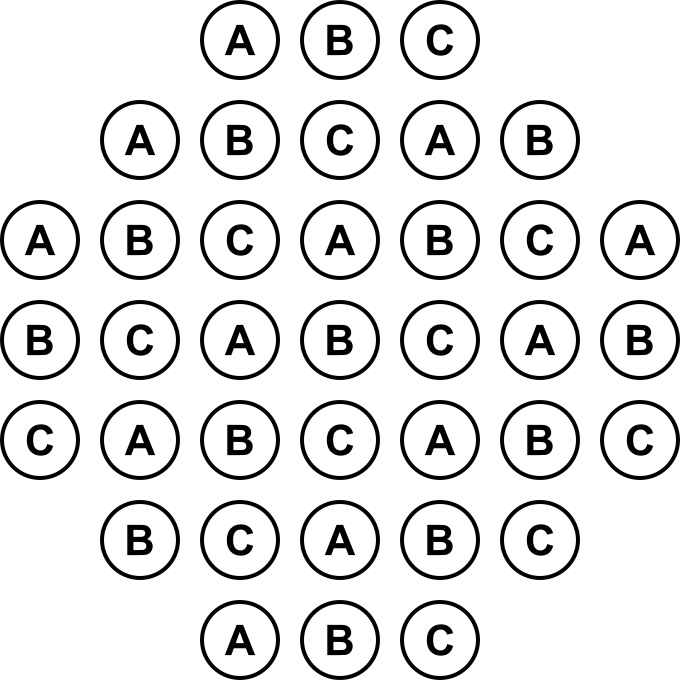
Hans Zantema (1956) matematikari eta informatikari herbeheretarrak, Nijmegeneko Radboud Unibertsitateko irakasleak, lerro batzuetan erakuts daitekeen froga dotore bat egin du, taulako posizioak A, B eta C letrekin (letra bakoitza diagonal batean eta letrak txandakatuz) honela izendatuta:
Taulako zentroko zulo libratuz hasten bagara, jokoaren hasieran 12 A posizio, 12 B posizio eta 12 C posizio fitxez beteta daude. Jauzi batek hiru diagonal hartzen ditu beti; beraz, hiru letren kopuruetan eragiten du, jauziaren muturretakoak eta tartekoa. Jauzi batek mututrretako bi letren kopuruak aldatzen ditu: fitxa posizio batetik kentzean, posizio horretako latraren kopurua txikitzen da (-1) eta, fitxa posizio batean jartzean, posizio horretako letraren kopurua handitzen da (+1); bestalde, tarteko posizioan hirugarren letra dagoenez eta taulatik kentzen denez, letra horren kopurua txikitzen da (-1). Ondorioz, kopuruak bikoitiak baziren, jauziaren ondoren bakoitiak izango dira, eta alderantziz. Hortaz, jauzi kopuru bikoiti baten ondoren, A posizio beteen kopurua bikoitia izango da, baita B eta C posizio beteena ere; eta jauzi kopuru bakoiti baten ondoren, A posizio beteen kopurua bakoitia izango da, baita B eta C posizio beteetarako ere.
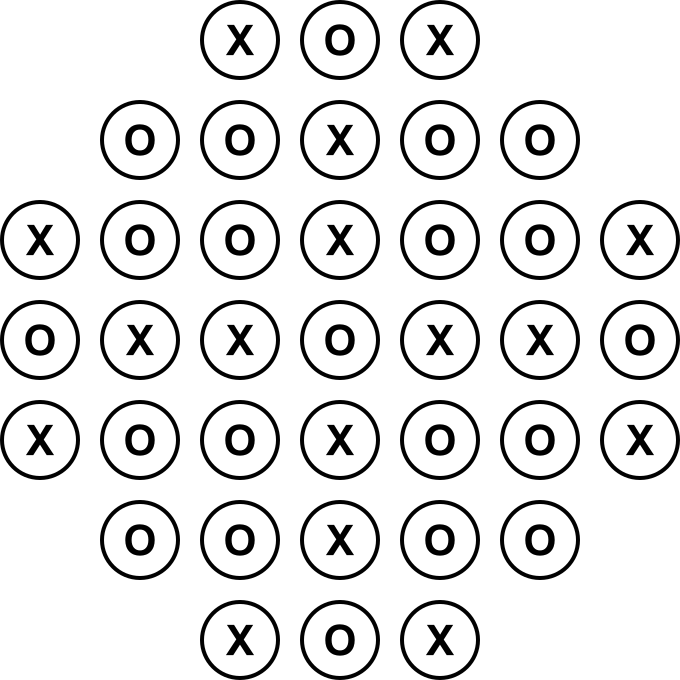
Bakar-joko frantsesaren taulak 37 zulo dituenez, zentroko fitxa kendu ondoren, 35 jauzi beharko lirateke fitxa bakar batera iristeko; beraz, A, B eta C posizioen kopuruek bakoitiak izan beharko lukete, eta hori ezinezkoa litzateke fitxa bakar batekin. Fitxa bakarra geratzen bada, letra baten kopurua 1, bakoitia, izango da; baina beste bi letren kopuruak 0, bikoitiak, dira.
Joko honetan, taulan bi fitxa uztea da emaitzarik onena.
Izan ere, 37 zuloko bakar-jokoan, lehenengo zulo hutsa diagrama honetan X batez markatutako posizioetako batean badago bakarrik dago soluzioa .
Iturriak
Patxi Angulo Martin: Mundu zabaleko jokoak. Jokoen mundu zabala. Elhuyar, Usurbil, 1997.
Robert Charles Bell: Board and Table Games from Many Civilizations, 1 eta 2. Dover Publications, Inc., New York, 1979.
David Parlett: History of Board Games. Echo Point Books & Media, Brattleboro, 1999.
Harold James Ruthven Murray: A History of Board-Games other than Chess. Oxford University Press, Oxford, 1951.
David Pritchard: The family book of games. Brockhampton press, Leicester, 1994.
José Manuel Espinel Cejas eta Francisco García-Talavera Casañas: Juegos guanches inéditos. Inscripciones geométricas en Canarias. Centro de la cultura popular canaria, Tenerife, 2009.
El Mundo de los Juegos (2). Altaya, Bartzelona, 1999.
Wikipedia.en
Wikipedia.fr
Ovidio: Ars Amatoria, https://la.wikisource.org/wiki/Ars_amatoria/Liber_III
